
第三章热力学第二定律 (Chapter 2 The Second Law of Thermodynamics) 教学 明确热力学第二定律的意义,了解自发变化的共同性质:了解第二定 目的律和卡诺定理的联系:掌握U、H、S、F、G的定义及其物理意义。明确△G 要求在特定条件下的意义及其判据作用:熟练地计算一些简单过程中的△S、 △H、△G及利用范特霍夫等温式判别化学反应的方向。熟练地运用吉布斯 一亥姆霍兹公式、克拉贝龙和克劳修斯一克拉贝 方程式,明确偏摩尔和 化学势的意义、热力学第三定律的意义及其相关计 教学 熵及Gibbs自由能的概念及运用 重点 教学熵概念的意义及基本热力学关系的应用 难点 教学系统讲授法,读书指导法等 方法 教学传统教学手段和现代化教学手段(多媒体课件)相结合 手段 教学12课时 时数§3.1热力学第二定律的表述,(1课时)§3.2卡诺原理(1课时): §3.3过程的热温熵与熵函数概念,§3.4过程方向与限度的判据,§ 3.5熵变的计算与熵判据的应用,§3.6熵的统计意义,§3.7热力学 第三定律规定嫡,§3.8自由能(4课时): §3.8自由能, §3.9△G的计算与应用(2课时) §3.9△G的计算与应用,§3.10热力学函数间的基本关系式,§3.11 多组分体系中物质的偏摩尔量和化学势§3.12气体体系中物质化学势, (4课时)。 第三章热力学第二定律 (Chapter 2 The Second Law of Thermodynamics) §3-1热力学第二定律的表述 能量转化守恒定律(热力学第一定律)的提出,根本上宣布第一类永动机是不能造
第三章 热力学第二定律 (Chapter 2 The Second Law of Thermodynamics) 教学 目的 要求 明确热力学第二定律的意义,了解自发变化的共同性质;了解第二定 律和卡诺定理的联系;掌握U、H、S、F、G的定义及其物理意义。明确∆G 在特定条件下的意义及其判据作用;熟练地计算一些简单过程中的∆S、 ∆H、∆G及利用范特霍夫等温式判别化学反应的方向。熟练地运用吉布斯 -亥姆霍兹公式、克拉贝龙和克劳修斯-克拉贝龙方程式,明确偏摩尔和 化学势的意义、热力学第三定律的意义及其相关计算。 教学 重点 熵及Gibbs自由能的概念及运用 教学 难点 熵概念的意义及基本热力学关系的应用 教学 方法 系统讲授法,读书指导法等 教学 手段 传统教学手段和现代化教学手段(多媒体课件)相结合 教学 时数 12课时 §3.1 热力学第二定律的表述,(1课时) §3.2 卡诺原理(1课时); §3.3 过程的热温熵与熵函数概念, §3.4 过程方向与限度的判据, § 3.5 熵变的计算与熵判据的应用,§3.6 熵的统计意义, §3.7 热力学 第三定律 规定熵,§3.8 自由能(4课时); §3.8 自由能, §3.9 Δ G 的计算与应用(2课时); §3.9 Δ G 的计算与应用, §3.10 热力学函数间的基本关系式, §3.11 多组分体系中物质的偏摩尔量和化学势 §3.12 气体体系中物质化学势, (4课时)。 第三章 热力学第二定律 (Chapter 2 The Second Law of Thermodynamics) §3-1热力学第二定律的表述 能量转化守恒定律(热力学第一定律)的提出,根本上宣布第一类永动机是不能造

出的。但不违背热力学第一定律的过程是否就能发生呢?例如: 0 T2- →T1T1<T2) Zn+CuSOa(aq)ZnSO(aq)+Cu AHm*=-216.8 kJ mol- 热力学第二定律所要解决的问题是寻找一个在一定条件下的过程进行的共同判 据、 普遍适用的判据 这个判据一定是体系的状态函数。它的改变值反映在一定条件下过程的方向性。 一热力学第二定律的表述(Expression of Second Law of Thermodynamics) 1824年Carnoti认为热机必须在两个热源间工作,从高温热源吸热只有部分作功, 而其余部分传给低温热源。 *1851年开尔文(Kelvin): 不可能从单一热源吸取热量使之完全转化为功而不引起其他变化。 热力学第二定律的确立,证明第二类永动机是不可造出的。第二类永动机: 一科 能够从单一热源吸热,并将所吸收的热全部变为功而无其他影响的机器(Second Kind of permanent motion machine 上述两种表达方法是完全有效的。 设有一部违反Kelvinz热机A和制冷机B联合工作,如下图: %=四2+g 0. 于是联合工作的净结果就是从低温热源传到高温物体而不产生其他影响。这就 违反了克劳修斯的表达。 上图(右)是违反Clāusius表述的A机,联合工作的净结果是从高温热源吸收的 (Q,-|QI)的热完全转变为功而不产生其他影响。这就违反了Kelvin表述。 热力学第二定律深刻地揭示了热功转化的辩证关系: 功可以全部转变为热而不留下其他变化,而热却不能。因此热和功的转化是不 可逆的,是有方向性的。 例 ①理想气体的真空膨胀(Q=0,W=0),然后压缩,功→热(环境) ②T2>T1T2 T,A为制冷机,功热(环境)
出的。但不违背热力学第一定律的过程是否就能发生呢?例如: 热力学第二定律所要解决的问题是寻找一个在一定条件下的过程进行的共同判 据-普遍适用的判据。 这个判据一定是体系的状态函数。它的改变值反映在一定条件下过程的方向性。 一热力学第二定律的表述 (Expression of Second Law of Thermodynamics) 1824年Carnot认为热机必须在两个热源间工作,从高温热源吸热只有部分作功, 而其余部分传给低温热源。 * 1850年克劳修斯(R.Clausius): 不可能把热从低温物体传到高温物体而不产生其他影响。 * 1851年开尔文(Kelvin): 不可能从单一热源吸取热量使之完全转化为功而不引起其他变化。 热力学第二定律的确立,证明第二类永动机是不可造出的。第二类永动机:一种 能够从单一热源吸热,并将所吸收的热全部变为功而无其他影响的机器(Second Kind of permanent motion machine) 上述两种表达方法是完全有效的。 设有一部违反Kelvin热机A和制冷机B联合工作,如下图: 于是联合工作的净结果就是从低温热源传到高温物体而不产生其他影响。这就 违反了克劳修斯的表达。 上图(右)是违反Clausius表述的A机,联合工作的净结果是从高温热源吸收的 (Q2-|Q1|)的热完全转变为功而不产生其他影响。这就违反了Kelvin表述。 热力学第二定律深刻地揭示了热功转化的辩证关系: 功可以全部转变为热而不留下其他变化,而热却不能。因此热和功的转化是不 可逆的,是有方向性的。 例: ① 理想气体的真空膨胀(Q=0,W=0),然后压缩,功

1)电解 ③H,00)= 2燃烧,8120,g) 1)W。=3.7kJ 2)W=3.7k Q=-285.8kJ Q285.8k 环境付出功:(270.9+3.7)274.6KJ 得到的热:274.6KJ ABRIPVABIrPV 二,自发过程和非自发过程 Gibs定义:凡是在理论上或实际上能够提供非体积功(体系环境)的过程是自 发的。由环境提供非体积功去使过程发生的则为非自发的。→ 例子: 焦耳的热功当量实验: 气体的真空膨胀: 高温物体到低温物体的热传递: 浓溶液的扩散等。 实际发生的过程无论自发还是非自发的,都是热力学不可逆的。(功一热)但反 之是违反热力学第二定律的 南大物化的定义(96):所谓自发变化”乃指能够自动发生的变化,而无需外 力帮助,任其自然,不去管它而可发生的变化。而其上述过程是非自发的。 §3-2卡诺原理 卡诺循环是卡诺热机的原理 任意热机 n=9+03-7 卡诺热机: T: IQ+Q.I=IW I 卡诺原理:工作于两个不同温度之间的所有热机,以卡诺可逆热机的工作效率为 最大,其工作效率只决定于两个热源的温度,与工作物质无关。 同样用反证法证明
ABR1pVABIrpV 二.自发过程和非自发过程 Gibbs定义:凡是在理论上或实际上能够提供非体积功(体系环境)的过程是自 发的。由环境提供非体积功去使过程发生的则为非自发的。 例子: 焦耳的热功当量实验; 气体的真空膨胀; 高温物体到低温物体的热传递; 浓溶液的扩散等。 实际发生的过程无论自发还是非自发的,都是热力学不可逆的。(功→热)但反 之是违反热力学第二定律的。 南大物化的定义(p96):所谓“自发变化”乃指能够自动发生的变化,而无需外 力帮助,任其自然,不去管它而可发生的变化。而其上述过程是非自发的。 §3-2 卡诺原理 卡诺循环是卡诺热机的原理 任意热机: 卡诺热机: ︱Q2 +Q1︱=︱W︱ 卡诺原理:工作于两个不同温度之间的所有热机,以卡诺可逆热机的工作效率为 最大,其工作效率只决定于两个热源的温度,与工作物质无关。 同样用反证法证明
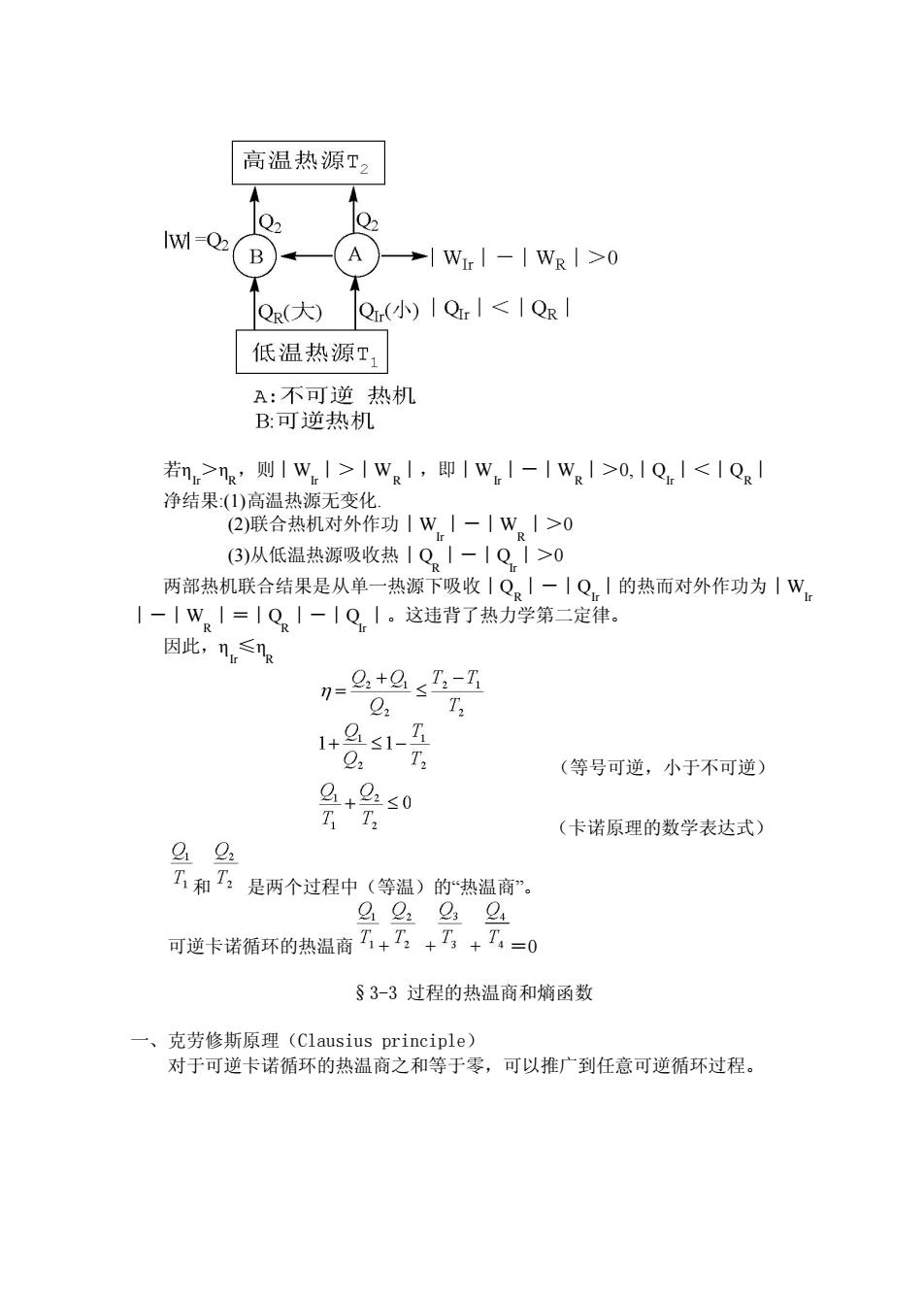
高温热源T2 Q IWI-B) A →|WI-IWR|>0 QR(大) Q(小)IQrI<IQR 低温热源工 A:不可逆热机 B:可逆热机 若n>ng'则1wI>IW.1,即|wI-IW|>0,|QI<IQg 净结果(1)高温热源无变化. 2)联合热机对外作功1W|一|WI>0 (3)从低温热源吸收热1Q。1-1Q.I>0 两部热机联合结果是从单一热源下吸收|Q。I一|Q|的热而对外作功为|W。 1-1W。1=1Q1-1Q1。这违背了热力学第二定律。 因此,n≤n 7=9+21-Z 22 02 (等号可逆,小于不可逆) 9+gs0 (卡诺原理的数学表达式) 92 T和T:是两个过程中(等温)的“热温商”。 可逆卡诺循环的热温商乙+了,+T+T,=0 §3-3过程的热温商和熵函数 一、克劳修斯原理(Clausius principle) 对于可逆卡诺循环的热温商之和等于零,可以推广到任意可逆循环过程
若ηIr >ηR,则︱W Ir︱>︱W R︱,即︱W Ir︱-︱W R︱>0,︱QIr︱<︱QR︱ 净结果:(1)高温热源无变化. (2)联合热机对外作功︱W Ir ︱-︱W R ︱>0 (3)从低温热源吸收热︱Q R ︱-︱Q Ir ︱>0 两部热机联合结果是从单一热源下吸收︱QR︱-︱QIr︱的热而对外作功为︱W Ir ︱-︱W R ︱=︱Q R ︱-︱Q Ir ︱。这违背了热力学第二定律。 因此,ηIr ≤ηR (等号可逆,小于不可逆) (卡诺原理的数学表达式) 和 是两个过程中(等温)的“热温商”。 可逆卡诺循环的热温商 + + + =0 §3-3 过程的热温商和熵函数 一、克劳修斯原理(Clausius principle) 对于可逆卡诺循环的热温商之和等于零,可以推广到任意可逆循环过程

任意可逆循环 W:A→B台AifB C→D台CkhD AU:AU B=AU Q:QB-QQr OCD-OCKD-OK +9a=0 ABCD台ifhk 任意可逆循环 克修斯原理(Clausius principle):任意可逆循环过程的热温商的总和等于零。 二、可逆过程的热温熵一熵变
W: A → B ⇔ AifB C → D⇔ CkhD ∆U:∆U AB =∆U Q: Q AB =Q A ifB =Q if QCD =QCkhD =Qkh ABCD ⇔ ifhk 克修斯原理(Clausius principle):任意可逆循环过程的热温商的总和等于零。 二、可逆过程的热温熵-熵变