
号=0 +受-0 - 两个积分值与途径无关,只与终始态有关,代表了两个体系在A、B两个状态之间 个状态函数之差值。该状态函数定义为嫡(entropy),S。 R AS=S。-S.=AT 表明熵值的改变等于任一可逆过程的热温熵之和 ds=S。-S=T 熵的单位是:JK 三、不可逆过程的热温嫡与熵变 1.不可逆过程的热温熵 (分析不可逆过程的热温熵和熵的关系)》 n≤nn 2+9T,-I 有 T 何定保.号会0
两个积分值与途径无关,只与终始态有关,代表了两个体系在A、B两个状态之间 一个状态函数之差值。该状态函数定义为熵(entropy),S。 ∆S=S B -S A = 表明熵值的改变等于任一可逆过程的热温熵之和。 dS= S B-S A= 熵的单位是: J K -1 三、不可逆过程的热温熵与熵变 1.不可逆过程的热温熵 (分析不可逆过程的热温熵和熵的关系) ηIr ≤ηR 有 不可逆循环:
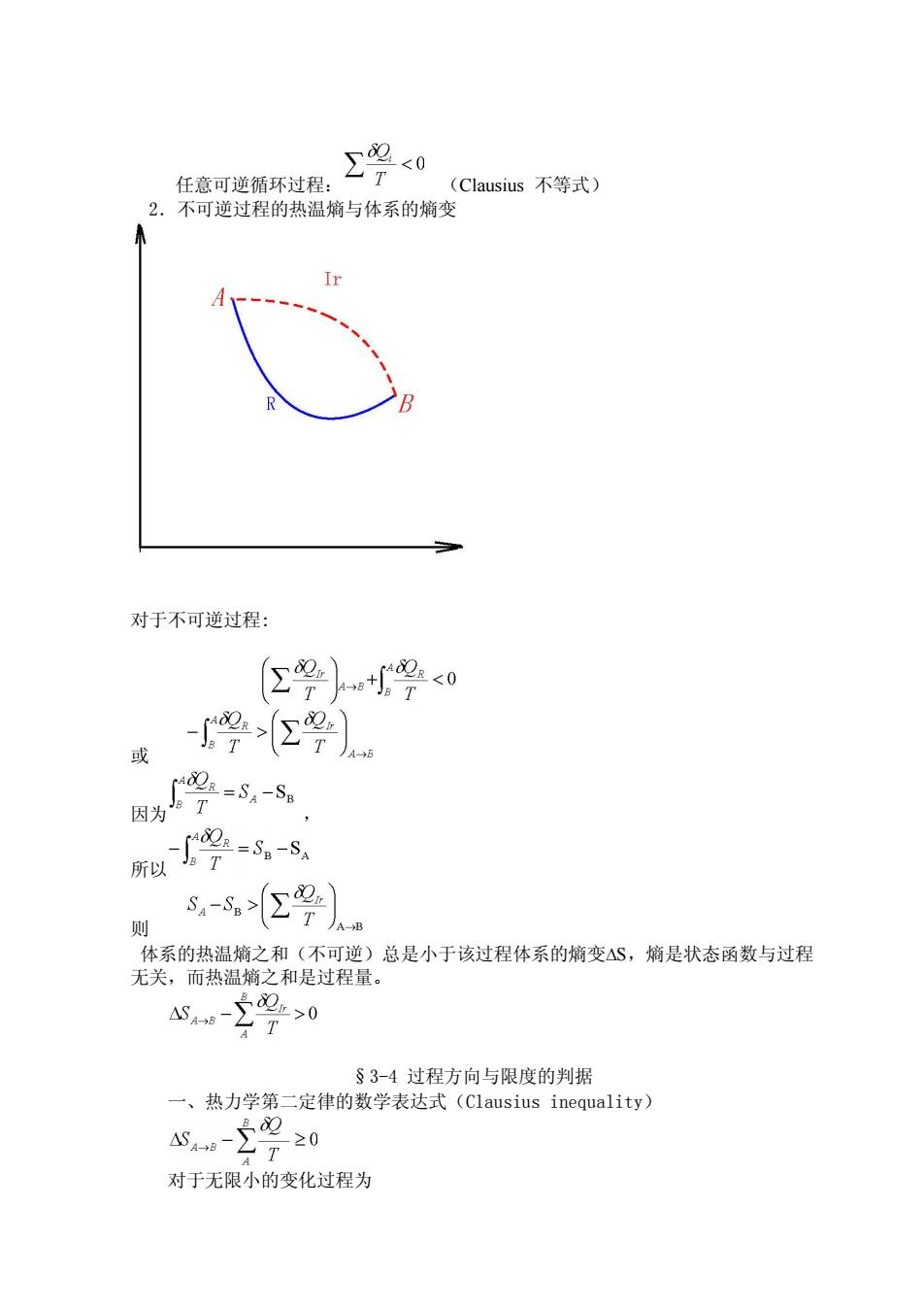
任意可逆循环过程 ∑%<0 Clausius不等式) 2.不可逆过程的热温熵与体系的嫡变 对于不可逆过程: 公2)+小2<0 9) 学5 成 和学8 则 s-号) 体系的热温熵之和(不可逆)总是小于该过程体系的熵变△S,熵是状态函数与过程 无关,而热温熵之和是过程量。 §3-4过程方向与限度的判据 一、热力学第二定律的数学表达式(Clausius inequality) A9-220 T 对于无限小的变化过程为
任意可逆循环过程: (Clausius 不等式) 2.不可逆过程的热温熵与体系的熵变 对于不可逆过程: 或 因为 , 所以 则 体系的热温熵之和(不可逆)总是小于该过程体系的熵变∆S,熵是状态函数与过程 无关,而热温熵之和是过程量。 §3-4 过程方向与限度的判据 一、热力学第二定律的数学表达式(Clausius inequality) 对于无限小的变化过程为

西-号20 (=”表示可逆过程,”表示不可逆过程,实际过程) 实际过程都是不可逆的,只能沿着热温熵之和小于体系的熵变的方向进行,而热 温熵之和大于体系的熵变的过程是不可能发生的。它可以判定实际过程的方向。 的值的大小作为不可逆程度大小的判据。 二、嫡增加原理 绝热体系Q=0,因而T=0,故 △地之0 表明在绝热条件下,任何实际过程沿着体系的熵值增大的方向进行,体系绝热可 逆过程中嫡值不变.因而绝热体系的嫡减小的过程是不可能的。这就是嫡增加原理(第 一定律的推论) 孤立体系是绝热的, ASv020 U,V一定,We=W。=0,“>”实际过程,“=”处于平衡态 孤立体系内的一切实际过程都是向着体系的熵增大的方向进行直到体系具有极 大值(dS=O)时到达平衡态显然孤立体系发生的实际过程都一定是自发的孤立体系 内的自发过程总是朝着熵值增大的方向进行。 个孤立体系的熵永不减 、”是增加原理的另一说法。 如果把和体系密切相关的部分包括在一起看作一个孤立体系则有: △S和立=△S体系+△S环境2 对于极大的环境, “=-名-% 任何自发过程都是由非平衡态趋向于平衡态,到达平衡态时熵函数有最大值。因 此自发过程进行的限度是以熵函数达到最大为准则。函数的数值就表征了体系接近 于平衡态的程度。 平衡态,非平衡态,介稳平衡态: 孤立体系内所发生的实际过程由初态→平衡态,其初态有一定限制存在下的平衡 态:介稳平衡态。介稳平衡态的热力学函数有确定的值。 §3-5嫡变的计算及嫡判据的应用 判定过程能否发生的步骤A→B 1.计算,选择可逆过程△S4
(“=”表示可逆过程,“>”表示不可逆过程,实际过程) 实际过程都是不可逆的,只能沿着热温熵之和小于体系的熵变的方向进行,而热 温熵之和大于体系的熵变的过程是不可能发生的。它可以判定实际过程的方向。 用 的值的大小作为不可逆程度大小的判据。 二、熵增加原理 绝热体系Q=0,因而 =0,故 表明在绝热条件下,任何实际过程沿着体系的熵值增大的方向进行,体系绝热可 逆过程中熵值不变。因而绝热体系的熵减小的过程是不可能的。这就是熵增加原理(第 二定律的推论)。 孤立体系是绝热的, U,V一定,We =W f =0,“>”实际过程,“=”处于平衡态 孤立体系内的一切实际过程都是向着体系的熵增大的方向进行直到体系具有极 大值(dS=0)时到达平衡态.显然孤立体系发生的实际过程都一定是自发的.孤立体系 内的自发过程总是朝着熵值增大的方向进行。 “一个孤立体系的熵永不减小”是熵增加原理的另一说法。 如果把和体系密切相关的部分包括在一起看作一个孤立体系则有: 对于极大的环境, 任何自发过程都是由非平衡态趋向于平衡态,到达平衡态时熵函数有最大值。因 此自发过程进行的限度是以熵函数达到最大为准则。熵函数的数值就表征了体系接近 于平衡态的程度。 平衡态,非平衡态,介稳平衡态: 孤立体系内所发生的实际过程由初态→平衡态,其初态有一定限制存在下的平衡 态:介稳平衡态。介稳平衡态的热力学函数有确定的值。 §3-5 熵变的计算及熵判据的应用 判定过程能否发生的步骤 1.计算,选择可逆过程

A8-广2 子利定过程的物之学 3.利用Clausius inequality AS≥∑9 判定过程”不可逆过程,“=”可逆,“<”不可能 一.无化学变化和无相变的变温过程(物理过程) 可逆变温过程:T环境一T体系=d7 80=Cd7 1.等容变温2。=nCv dI AS="7 2.等压变温0=nCd7 A="7n 3.理想气体状态变化(仅有体积功形=-∫PdW=-pa -dU-W=dU+pdv=nCv dT+nRr dV 于是 s=j9-"r+gav=c2+aRm号 60R=dU-oWR =dH-p叨-δW dH-d(pv)pdv =nCpmdT-Vdp AS-小2=mCnh子-mg P 计算△S时选择了特定的过程,但上二式与过程的可逆过程与否无关,因为嫡是状 态函粉 例1:(p61)
2.计算给定过程的热温熵 3.利用Clausius inequality 判定过程“>”不可逆过程,“=”可逆,“<”不可能 一.无化学变化和无相变的变温过程(物理过程) 可逆变温过程: 1. 等容变温 2.等压变温 3.理想气体状态变化(仅有体积功 ) 于是 计算∆S时选择了特定的过程,但上二式与过程的可逆过程与否无关,因为熵是状 态函数。 例1:(p61)

1molB(理气)一 真空→lmol(理气 200KPa 11.2cm △S=? 299a 解与过程无关 A=-Ra合=834h3w-57aK 真空膨胀W=0,Q=0是孤立体系。△S>0,说明一切实际过程都是不可逆的。 例2(p61) 273K 273K 101KPa 202KPa 22.4dm3 △S=? 11.2dm3 AS-RI -83142-50 W=-∫pdW=-P(V2-V)=-202×10311.2-22.40×103=2.38KJ ∑0-238x10 273 -8.35KJ s上9-5g-=200 (AU=Q+W=0) 可逆相变:两相平衡下的相变,即正常相变点时的相变。 Q。:可逆相变热 例3:(p62) 能否用判据,(绝热或孤立体系)△S之0 Q=AH=AH+△H,+△H 说明该过程是不可能发生,该过程的逆过程是可能发生的(热力学上)。 三、等温下化学反应的S 必须将此反应在等温可逆原电池中进行,即原电池在等温可逆过程所放出的热 或吸收的热。2a 例4:(p62) 解(1)因为等温下可逆原电池中进行反应,故
解 与过程无关: 真空膨胀W = 0,Q = 0是孤立体系。∆S>0,说明一切实际过程都是不可逆的。 例2 (p61) (∆U=Q+W=0) ∆S= 是一种实际发生的不可逆压缩过程。 二、相变过程 可逆相变:两相平衡下的相变,即正常相变点时的相变。 Q R :可逆相变热 例3:(p62) 能否用判据,(绝热或孤立体系) Qp =∆H=∆H 1 +∆H 2 +∆H 3 说明该过程是不可能发生,该过程的逆过程是可能发生的(热力学上)。 三、等温下化学反应的∆S 必须将此反应在等温可逆原电池中进行,即原电池在等温可逆过程所放出的热 或吸收的热。 例4:(p62) 解 (1) 因为等温下可逆原电池中进行反应,故