
3.2.2力对轴的矩
Fz Fx Fy 3.2.2 力对轴的矩
3.2.2力对轴的矩 力F对z轴的矩定义为: M.(F)=Mo(Fy)=tFh=+2A0ab 力对轴的矩是力使刚体绕该轴转动效果 的度量,是一个代数量,其绝对值等于 力在垂直于该轴平面上的投影对于轴与 平面交点的矩。 符号规定:从轴正向看,若力使则体逆时针转则取正号,反之 取负。也可按右手螺旋法则确定其正负号。 由定义可知:()当力的作用线与轴平行或相交(共面)时,力 对轴的矩等于零。(2)当力沿作用线移动时,它对于轴的矩不变
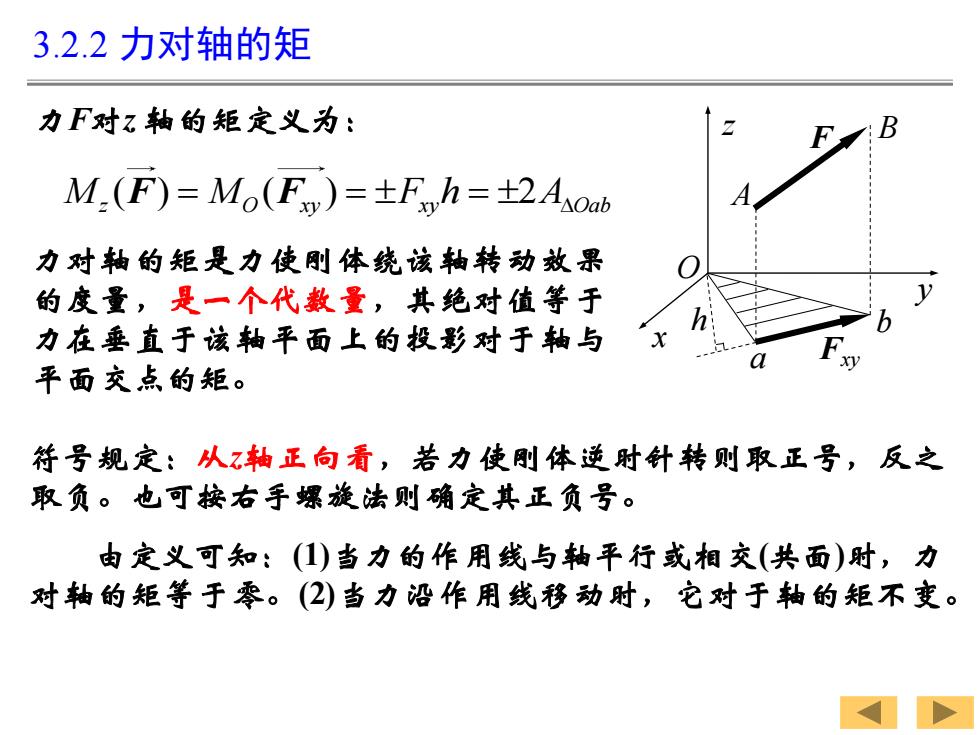
力F对z 轴的矩定义为: ( ) ( ) 2 M M F h A z O xy xy Oab F F = = = 力对轴的矩是力使刚体绕该轴转动效果 的度量,是一个代数量,其绝对值等于 力在垂直于该轴平面上的投影对于轴与 平面交点的矩。 3.2.2 力对轴的矩 x y z O F Fxy h B A a b 符号规定:从z轴正向看,若力使刚体逆时针转则取正号,反之 取负。也可按右手螺旋法则确定其正负号。 由定义可知:(1)当力的作用线与轴平行或相交(共面)时,力 对轴的矩等于零。(2)当力沿作用线移动时,它对于轴的矩不变

3.2.3力对轴的矩的解析表达式 设力F沿三个坐标轴的分量分别为Fx, Fy,F,力作用点A的坐标为cy,则 M.(F)=Mo(F) =Mo(F)+Mo(F.) =xF,-yF 同理可得其它两式。故有 M,(F)=yF:-zF, M,(F)=2F,-xF. M.(F)=xF-yF
3.2.3 力对轴的矩的解析表达式 x y z O F Fx Fy Fz A(x,y,z) B Fx Fy Fxy a b x y ( ) ( ) ( ) ( ) z O xy O x O y y x M M M M xF yF = = + = − F F F F 设力F沿三个坐标轴的分量分别为Fx, Fy,Fz,力作用点A的坐标为(x,y,z),则 同理可得其它两式。故有 ( ) ( ) ( ) x z y y x z z y x M yF zF M zF xF M xF yF = − = − = − F F F Fxy

3.2.4力对点的矩与力对过该点的轴的矩的关系 比较力对点的矩和力对轴的矩的解析表达式得: [M(F)],=M,(F) [Mo(F)],=M,(F) [Mo(F)].=M(F) 即:力对点的矩失在通过该点的某轴上的投影,等于力 对该轴的矩。 M,(F)=yF:-zF Mo(F)=r×市= y FF F M (F)=zF.-xF. =(yF.-2F)i+(zF-xF)j+(xF,-yF,)k M.(F)=xF,-yF
比较力对点的矩和力对轴的矩的解析表达式得: 即:力对点的矩矢在通过该点的某轴上的投影,等于力 对该轴的矩。 3.2.4 力对点的矩与力对过该点的轴的矩的关系 [ ( )] ( ) [ ( )] ( ) [ ( )] ( ) O x x O y y O z z M M M = = = M F F M F F M F F ( ) ( ) ( ) x z y y x z z y x M yF zF M zF xF M xF yF = − = − = − F F F ( ) ( ) ( ) ( ) O x y z z y x z y x x y z F F F yF zF zF xF xF yF = = − + − + − i j k M F r F = i j k
求力F在三轴上的投影和对三轴的矩。 解: Fa F Fcos0coso= va2+b2+c2 F,-Fcosesing= Fb b c0s0= Va+b2 -Fc F.=-Fsin0=- va2+b2+c 2 a2+b2+c2 M (F)=M(F)+M(F)+M,(F.)=-F.c M,(F)=0 M.(F)=M.(F)+M.(F,)+M.(F.)=-Fa
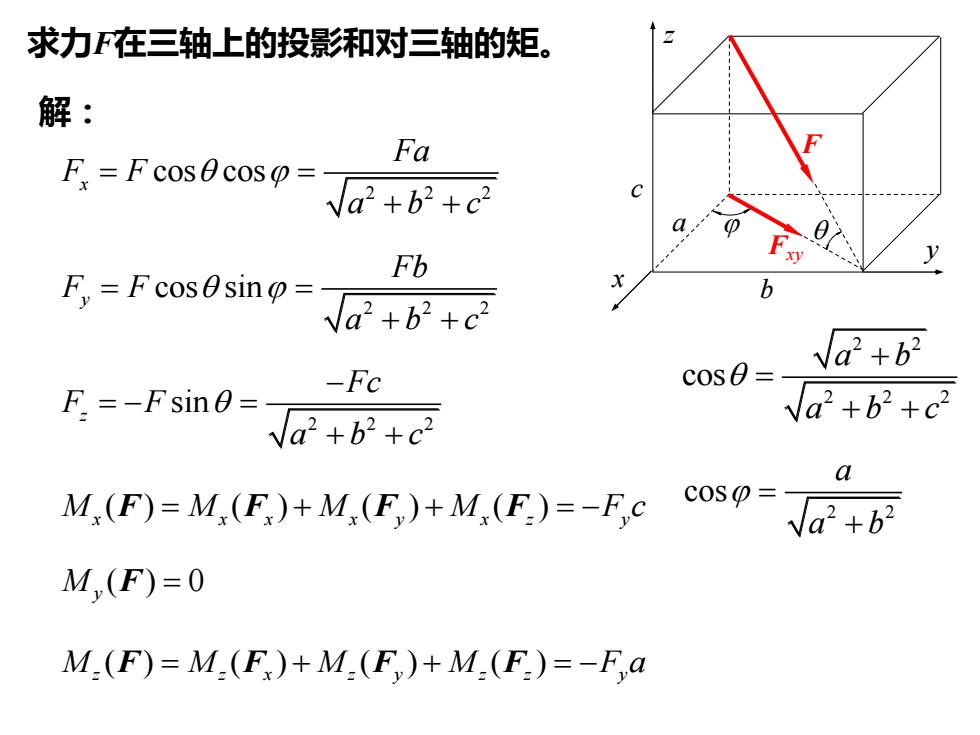
求力F在三轴上的投影和对三轴的矩。 解: 2 2 2 cos cos x Fa F F abc = = j + + 2 2 2 cos sin y Fb F F abc = = j + + 2 2 2 sin z Fc F F abc − = − = + + ( ) ( ) ( ) ( ) M M M M F c x x x x y x z y F F F F = + + = − ( ) 0 M y F = ( ) ( ) ( ) ( ) M M M M F a z z x z y z z y F F F F = + + = − y x z F j b c a Fxy 2 2 2 2 2 cos a b abc + = + + 2 2 cos a a b j = +