
第一节整数规划及其数学模型 松弛问题作为一个线性规划问题,其可行解 的集合是一个凸集,任意两个可行解的凸组合仍 为可行解。整数规划问题的可行解集合是它的松 弛问题可行解集合的一个子集,任意两个可行解 的凸组合不一定满足整数约束条件,因而不一定 仍为可行解。由于整数规划问题的可行解一定也 是它的松弛问题的可行解(反之则不一定),所 以,整数规划问题最优解的目标函数值不会优于 松弛问题最优解的目标函数值
8 松弛问题作为一个线性规划问题,其可行解 的集合是一个凸集,任意两个可行解的凸组合仍 为可行解。整数规划问题的可行解集合是它的松 弛问题可行解集合的一个子集,任意两个可行解 的凸组合不一定满足整数约束条件,因而不一定 仍为可行解。由于整数规划问题的可行解一定也 是它的松弛问题的可行解(反之则不一定),所 以,整数规划问题最优解的目标函数值不会优于 松弛问题最优解的目标函数值。 第一节 整数规划及其数学模型

第一节整数规戈划及其数学模型 在一般情况下,松弛问题的最优解不会刚好 满足变量的整数约束条件,因而不是整数规划的 可行解,自然就不是整数规划的最优解。此时, 若对松弛问题的这个最优解中不符合整数要求的 分量简单地取整数,所得到的解不一定是整数规 划问题的最优解,甚至还不一定是整数规划问题 的可行解
9 在一般情况下,松弛问题的最优解不会刚好 满足变量的整数约束条件,因而不是整数规划的 可行解,自然就不是整数规划的最优解。此时, 若对松弛问题的这个最优解中不符合整数要求的 分量简单地取整数,所得到的解不一定是整数规 划问题的最优解,甚至还不一定是整数规划问题 的可行解。 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 例1考虑下面的整数规划问题 max Z=x+4x2 -2x1+3x2≤3 x1+2x2≤8 x1x2 ≥0且取整数 画出可行域见图41。在图4-1中,四边形 OBPC及其内部的点为松弛问题的可行域,其中 那些整数格点为整数规划问题的可行解。根据目 标函数等值线的优化方向,P点(x=187, x2=19/7)就是其松弛问题的最优解,z=94/7
10 画出可行域见图4-1 。在图4-1中,四边形 OBPC及其内部的点为松弛问题的可行域,其中 那些整数格点为整数规划问题的可行解。根据目 标函数等值线的优化方向 , P 点 ( x1 =18/7, x2 =19/7)就是其松弛问题的最优解,z=94/7。 + − + = + , 0且取整数 2 8 2 3 3 max 4 1 2 1 2 1 2 1 2 x x x x x x Z x x 例1 考虑下面的整数规划问题: 第一节 整数规划及其数学模型
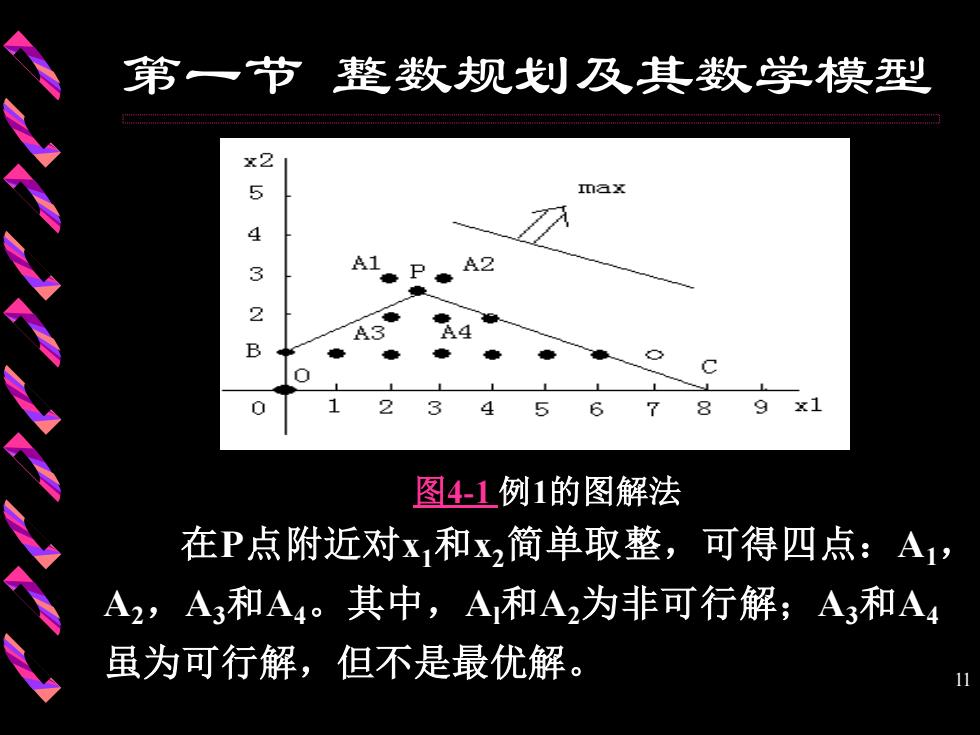
第一节整数规划及其数学模型 x2 5 max 4 3 A2 2 B 9 x1 图41例1的图解法 在P点附近对x和x简单取整,可得四点:A1, A2,A3和A4。其中,A和A2为非可行解;A3和A4 虽为可行解,但不是最优解
11 在P点附近对x1和x2简单取整,可得四点:A1, A2,A3和A4。其中,Al和A2为非可行解;A3和A4 虽为可行解,但不是最优解。 图4-1 例1的图解法 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 本例整数规划的最优解为A*点(区1=4,x22) 其目标函数值Z=12。 由于整数规划及其松弛问题之间的上述特殊 关系,像例4先求松驰问题最优解,再用简单取整 的方法虽然直观简单,却并不是求解整数规划的 有效方法。 12
12 本例整数规划的最优解为A*点(x1 =4,x2 =2), 其目标函数值Z =12。 由于整数规划及其松弛问题之间的上述特殊 关系,像例4先求松弛问题最优解,再用简单取整 的方法虽然直观简单,却并不是求解整数规划的 有效方法。 第一节 整数规划及其数学模型