
Review 矢量分析与场论 静电场 恒定电流的电场 ■恒定电流的磁场 静态场的解 时变电磁场 平面电磁波 ■电磁波的辐射 XIDIAN.EDU.CN lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 2 Review 矢量分析与场论 静电场 恒定电流的电场 恒定电流的磁场 静态场的解 时变电磁场 平面电磁波 电磁波的辐射 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

矢量分析与场论 场的基本概念;标量场梯度;矢量场散度、旋度;亥姆霍 兹定理;圆柱坐标系与球坐标系中的梯度、散度和旋度。 1.基本要求 ·(1)熟练掌握场的基本概念,标量场梯度、矢量场散度和旋度 的定义、运算。 ·(2)了解圆柱坐标系与球坐标系中梯度、散度和旋度运算。 ■2.重点、难点 ·重点:场的基本概念; 梯度、散度和旋度的定义、运算和物 理意义 ·难点:矢性微分算符、亥姆霍兹定理、矢量公式。 V×(Vo)=0 梯无旋 7.(7×④=0 旋无散 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 3 矢量分析与场论 场的基本概念;标量场梯度;矢量场散度、旋度;亥姆霍 兹定理;圆柱坐标系与球坐标系中的梯度、散度和旋度。 1.基本要求 • (1)熟练掌握场的基本概念,标量场梯度、矢量场散度和旋度 的定义、运算。 • (2)了解圆柱坐标系与球坐标系中梯度、散度和旋度运算。 2.重点、难点 • 重点:场的基本概念;梯度、散度和旋度的定义、运算和物 理意义 • 难点:矢性微分算符、亥姆霍兹定理、矢量公式。 ∇⋅ ∇× = ( )0 A ∇× ∇ = ( )0 ϕ 旋无散 梯无旋 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
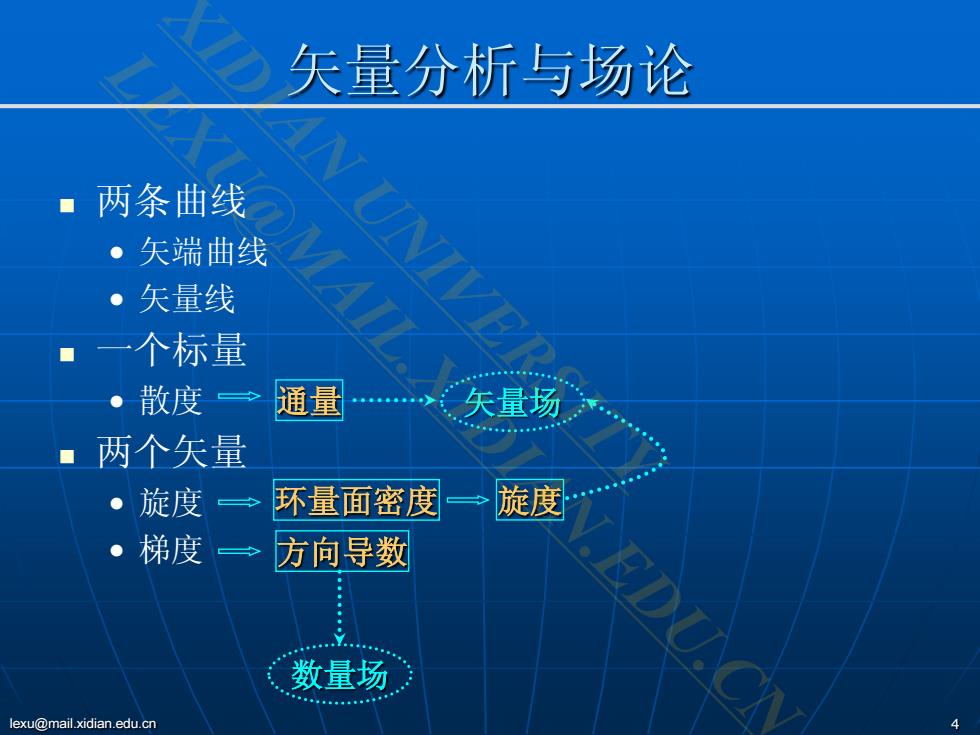
矢量分析与场论 ■两条曲线 ·矢端曲线 ·矢量线 一个标量 ·散度一 通量 矢量场 两个矢量 ·旋度一 环量面密度 旋度 。梯度→ 方向导数 数量场 .EDU.C lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 4 矢量分析与场论 两条曲线 • 矢端曲线 • 矢量线 一个标量 • 散度 两个矢量 • 旋度 • 梯度 通量 环量面密度 旋度 方向导数 矢量场 数量场 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

静电场 ■ 电荷;电场强度;静电场的通量与散度;静电场的环量与 旋度;静电场的基本方程;电位;泊松方程和拉普拉斯方 程;电偶极子及其产生的场:介质中的场方程;静电场的 边界条件;静电场中的多导体系统、多导体系统的部分电 容;静电场的能量、能量密度 基本要求 。熟练掌握静电场基本概念、静电场的基本方程、边界条件。 。掌握静电场计算方法、电场能量计算,电容的求解 重点、难点 ● 重点:静电场基本概念,静电场基本方程、边界条件的物理 意义和应用。 ·难点:由场源分布求静电场,电场能量、 电容的求解。 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn 5 静电场 电荷;电场强度;静电场的通量与散度;静电场的环量与 旋度;静电场的基本方程;电位;泊松方程和拉普拉斯方 程;电偶极子及其产生的场;介质中的场方程;静电场的 边界条件;静电场中的多导体系统、多导体系统的部分电 容;静电场的能量、能量密度 基本要求 • 熟练掌握静电场基本概念、静电场的基本方程、边界条件。 • 掌握静电场计算方法、电场能量计算,电容的求解 重点、难点 • 重点:静电场基本概念,静电场基本方程、边界条件的物理 意义和应用。 • 难点:由场源分布求静电场,电场能量、电容的求解。 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
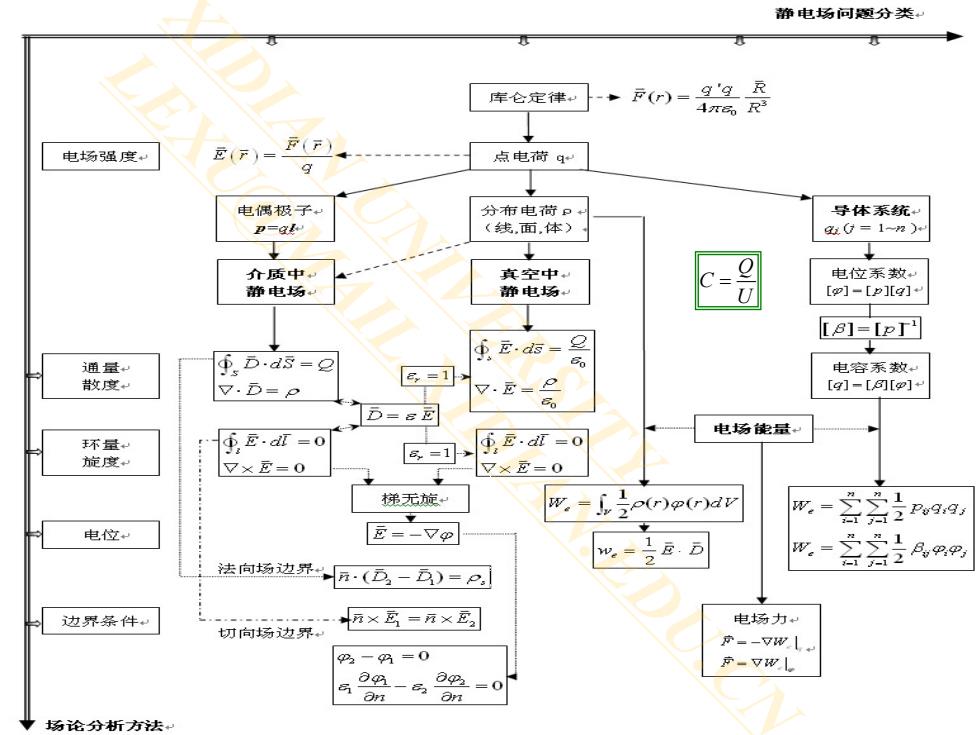
静电场问题分类 库仑定律和 ·F()=9'9元 4T岛R 电场强度 ()= 点电荷q 电偶极子 分布电荷只+ 导体系统 卫=g (线面体) 0=12) ↓ 介质中 真空中 电位系数 静电场 静电场 [p]-[p][g] [B]=[P ④Ds=2 fE.ds-2 通量 散度 V.D=p B=可入 电容系数 v.五=P [g]-[[o]+ ,D=s园 ∮E·r=0 电场能量 不量 E.dT =o 旋度 6=1 7×五=0 7×五=0 递无旋, w.=f fo(r)p(r)dv w- ””1 云209g 电位 五--7p w.=2.D w。= ”1 法向场边界“厅·(D-)=P, 云六2月9 边界条件 n×瓦=万×E2 电场力 切向场边界 京=-WL 22一码=0 声一V用 a 80 E On -=0 an 场论分析方法
lexu@mail.xidian.edu.cn 6 静电场 Q C U = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN