
21st 第9章 食品系列数材 浸出和萃取 本章的学习目的与要求 了解浸出的基本概念、浸出过程与浸出理论;了解常用的 几种浸出装置及其工作原理;掌握浸出速率的计算方法;重点 掌握浸出级数的求取方法;了解萃取的基本概念、萃取体系相 平衡及操作原理,了解萃取剂的选择原则;掌握萃取过程的基 本计算;重点掌握完全不互溶体系的有关计算;了解超临界萃 取的基本原理、超临界流体的特点;了解超临界萃取的一般流 程与应用

第9章浸出和萃取615 浸出和萃取是指加溶剂于混合物,利用溶剂对不同物质具有不同溶解度,从 而使混合物得到完全或部分分离的过程。如果被处理的混合物为固体,则为固 液萃取,即浸出或浸取;如果被处理的混合物为液体,则称为液一液萃取或萃 取。 无论混合物为固体或液体,在经溶剂处理后,其易溶解部分必将溶出而成为 溶液,达到分离的目的。物质由一相转入另一相的过程实为传质过程,因此,萃 取操作为传质过程之一 固一液萃取和液一液萃取其操作过程有所不同。在固体萃取中,溶质首先溶 解于溶剂,然后由固液两相的介面扩散到溶剂的主体。如以热水作为溶剂从甜菜 中萃取蔗糖,以酒精或汽油为溶剂从大豆中分离出食油等均为固一液萃取的例 子。在液体萃取中,溶剂与被处理的溶液互不相混合,但所用溶剂对于被处理溶 液中的溶质却有选择性的溶解能力,因而溶质可经由两液相间的界面,由一相扩 散到另一相。如动物脂肪的精炼,脂肪是一种液相,以溶剂来移去不需要的组 分,即为液一液萃取的例子。 由萃取而获得的物质不是纯物质而是溶液。为了获得纯物质还须作进一步的 处理,通常可借蒸馏、蒸发、结晶或干燥等方法,以去除萃取时所用的溶剂。为 了经济的原因,一般溶剂须回收重用。显然,若用的溶剂为水,则可不予回收。 1浸出 浸出是粮、油食品工业上的一个常见而重要的单元操作。由于食品原料多为 农产品,其组织和成分也极为复杂。另外,食品原料的质量还受品种、成熟度、 气候、产地及储藏条件的影响,特别是生物体所具有的蛋白质、碳水化合物、脂 肪、有机酸、酶等所受到的上述因素的影响更大。因此,浸出操作有很大的不 同,浸出操作的理论也就不可能用单纯的基础理论来概括。许多问题的解决主要 还是采用半经验或经验的办法来解决。 浸出过程一般包括:原料预处理(破碎或切片)、混合浸出和分离等过程

616食品工程原理 1.1浸出理论 1.1.1浸出体系组成的表示方法 浸出体系通常可简化为一个由三种组分组成的三元物系,既溶质A、溶剂S 和惰性固体B。溶质分布在固、液两相中,在固相中的溶质浓度和在液相中的溶 质浓度间必然存在一定的平衡关系。为了表示这种系统的组成,一般用三角形相 图表示三组分混合物的组成。常用的是等边三角形或等腰直角三角形相图,其中 以直角三角形最为简便,如图91所示。一般用质量分数表示组成(也可用摩尔 分数)。在三角形相图中,三个顶点分别表示三种纯组分,如图中A点表示溶质 A的组成为100%,其他两组分的组成为零。同理,B点和S点分别表示纯的惰 性固体和溶剂。 三角形任一边上的任一点则表示一个二元混合物,如AB边上的E点表示 A、B二元混合物,其中含A40%,B60%。 三角形内的某一点则代表一个三元混合物。如图91所示在直角三角形相图 中的M点即代表A、B、S三个组分组成的三元混合物,过M点分别作三个边 的平行线FG、HⅡ与JK,其线段BF(或SC)代表A的组成,线段A五(或BI) 及AJ(或SK)则分别表示S及B的组成。由图读得,该三元混合物的组成 为: xA=BF=0.30;xB=J=0.40;xs=AH=0.30 3种组分的的质量分率之和等于1,即: xA+xB+xs=0.30+0.40+0.30=1.00 其中xA、xB、xs分别代表3种组分的质量分数。本章组分表示,除另有说明 外,均用质量分数。 1.1.2浸出系统的平衡关系 浸出系统的平衡关系甚为复杂,其机理尚未搞清,按溶质A和溶剂S之间 的溶解情况,可分成三类:①A原来呈固态,则A在S中必有一饱和溶解度。 设该饱和溶解度即图9-2中的G点所代表的组成,则BG线把相图分为两个区 域,其中位于BG线下方的区域为不饱和区,亦即A与S量之比小于饱和溶解
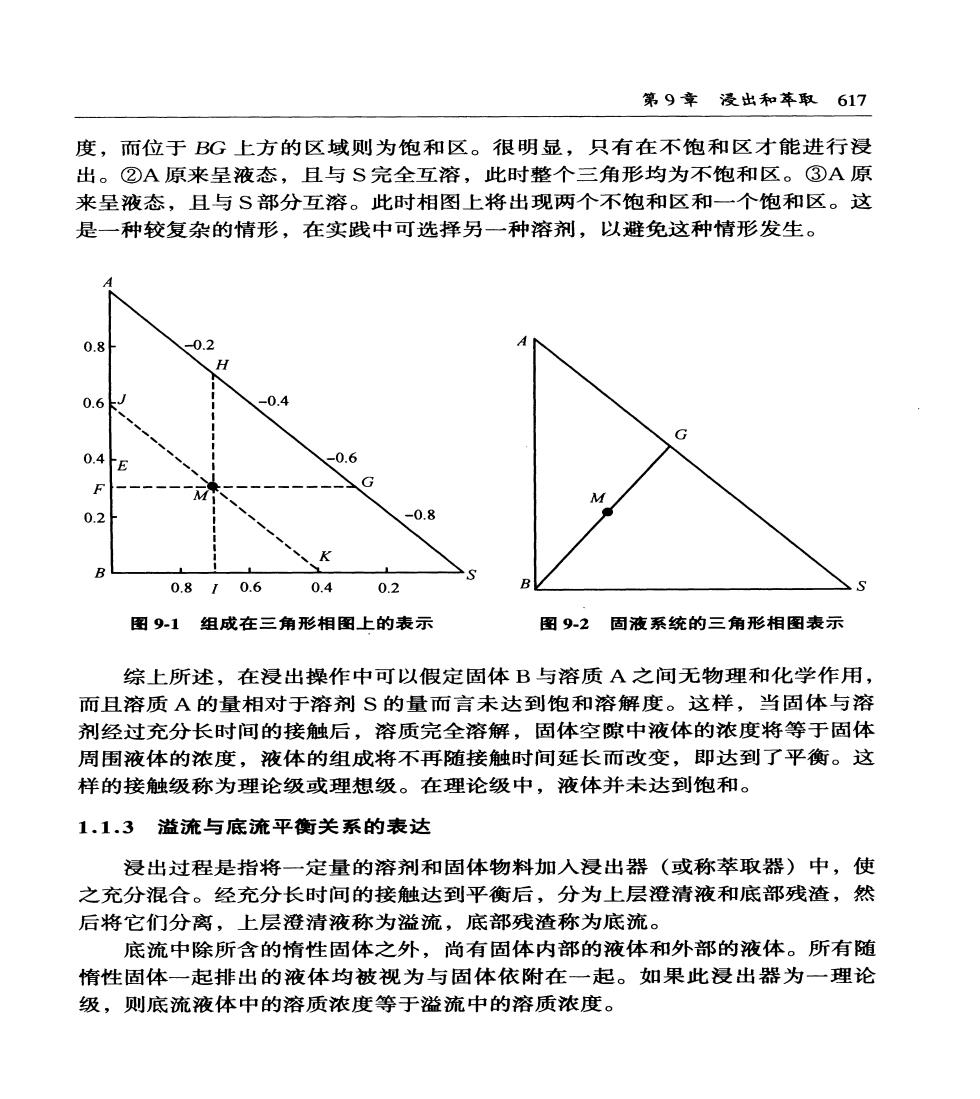
第9章浸出和车取617 度,而位于G上方的区域则为饱和区。很明显,只有在不饱和区才能进行浸 出。②A原来呈液态,且与S完全互溶,此时整个三角形均为不饱和区。③A原 来呈液态,且与S部分互溶。此时相图上将出现两个不饱和区和一个饱和区。这 是一种较复杂的情形,在实践中可选择另一种溶剂,以避免这种情形发生。 0.2 0. -0.4 G 0.4 0.6 0.2 0.8 、K 0.810.6 0.402 图91组成在三角形相图上的表示 图92固液系统的三角形相图表示 综上所述,在浸出操作中可以假定固体B与溶质A之间无物理和化学作用, 而且溶质A的量相对于溶剂S的量而言未达到饱和溶解度。这样,当固体与溶 剂经过充分长时间的接触后,溶质完全溶解,固体空隙中液体的浓度将等于固体 周围液体的浓度,液体的组成将不再随接触时间延长而改变,即达到了平衡。这 样的接触级称为理论级或理想级。在理论级中,液体并未达到饱和。 1.1.3溢流与底流平衡关系的表达 浸出过程是指将一定量的溶剂和固体物料加入浸出器(或称萃取器)中,使 之充分混合。经充分长时间的接触达到平衡后,分为上层澄清液和底部残渣,然 后将它们分离,上层澄清液称为溢流,底部残渣称为底流。 底流中除所含的惰性固体之外,尚有固体内部的液体和外部的液体。所有随 惰性固体一起排出的液体均被视为与固体依附在一起。如果此浸出器为一理论 级,则底流液体中的溶质浓度等于溢流中的溶质浓度

618食品工程原理 在三角形相图上,如果溢流中不含 惰性固体,则其组成点必位于AS边上, 如图9-3中E点。底流则可看做由一定 量的惰性固体和一部分夹带的其他组成 即与溢流相同的溶液混合而成,故其组 成必位于BE联线上,如图9-3,设其状 态点为R。 浸出操作可以连续进行,也可以间 歇进行,间歇操作时,各股物料的量以 kg表示;连续操作时,以质量流量kg/ s 表示。以yA表示溢流中溶质A的浓度, 以xA表示底流中溶质A的浓度。 图93浸出操作中溢流与底流的平衡 关系及单级浸出 1.1.4杠杆规则 在浸出操作计算中,平衡各相之间 的相对数量经常需要利用杠杆规则来确定,现将杠杆规则证明如下: 如图9-3,假设混合物量为M,其组成为zA、zB、zs;溢流E组成为yA、 B、ys;设底流的组成为BE联线上的R状态点,其组成为xA、xB、xs,则 总物料衡算 M=E+R (9-1) 对组分A的物料衡算MzA=EyA+RxA (9-2) 将式(9-1)代入式(9-2)并整理得 E(yA-A)=R (zA-A) 即 发-认卧 (9-3) 根据三角形相似定律,得 最玖款器即恶 式中:RM、ME分别为线段的长度;E、R分别为溢流和底流量,单位kg或kg/s (用状态点的符号同时表示该状态点的物料量,以下均用这种方法表示)。 同理,可得 后器&是 (9.4)