北京化工大学：《机械设计》课程教学资源（PPT课件）第三章 机械零件的强度

§3一2机械零件的疲劳强度计算（续) 2 图3-4 零件的极限应力线图

§3—2 机械零件的疲劳强度计算（续）

sity of C §3一2机械零件的疲劳强度计算（续) o直线AG的方程，由已知两点坐标A(0,o.11K)及D(Co /2,oo/2K)求得为 -L-Oo+Wame eK。 0或o1=K。oe+ynOm (3—9) o直线CG的方程为 0a'+0m′=0s(3-10) o式中：0ae 零件受循环弯曲应力时的极限应力幅： Ome 零件受循环弯曲应力时的极限平均应力； 零件受循环弯曲应力时的材料常数。 W oe 图3一4零件的极限应力线图

 直线AG的方程，由已知两点坐标A(0，σ-1 / Kσ)及D(σ0 ／2，σ0 / 2Kσ)求得为 或 (3—9) 直线CG的方程为  σa ＇+σm ＇=σs (3—10)  式中：σae ＇——零件受循环弯曲应力时的极限应力幅；  σme ＇——零件受循环弯曲应力时的极限平均应力；  ——零件受循环弯曲应力时的材料常数。 e ae e me K               1 1  K ae   me     1  e §3—2 机械零件的疲劳强度计算（续）

§3一2机械零件的疲劳强度计算（续) ym可用下式计算 "2=1.201-o6(3-11) K。K。 00 Kσ—弯曲疲劳极限的综合影响系数。 1 (3-12) 式中：k。一零件的有效应力集中系数： 零件的尺寸系数； Bo 零件的表面质量系数： 零件的强化系数。 图3-4零件的极限应力线图

 可用下式计算  (3—11)  Kσ——弯曲疲劳极限的综合影响系数。  e 0 1 2 1 0               K K e q k K       1 1 1           （3—12） 式中：kσ——零件的有效应力集中系数； εσ——零件的尺寸系数； βσ——零件的表面质量系数； βq——零件的强化系数。 §3—2 机械零件的疲劳强度计算（续）

Sty of C 15 §3一2机械零件的疲劳强度计算（续) 。(一)单向稳定变应力时机械零件的疲劳强度计算 。机械零件危险截面上的最大工作应力omax 0 最小工作应力omim, 。据此计算出工作平均应力om及工作应力幅oa,然后，在 极限应力线图的坐标上即可标示出相应于om及oa的一个 工作应力点M(或者点N)。 M D N me

 (一)单向稳定变应力时机械零件的疲劳强度计算  机械零件危险截面上的最大工作应力σmax  最小工作应力σmin，  据此计算出工作平均应力σm及工作应力幅σa，然后，在 极限应力线图的坐标上即可标示出相应于σm及σa的一个 工作应力点M(或者点N)。 §3—2 机械零件的疲劳强度计算（续）

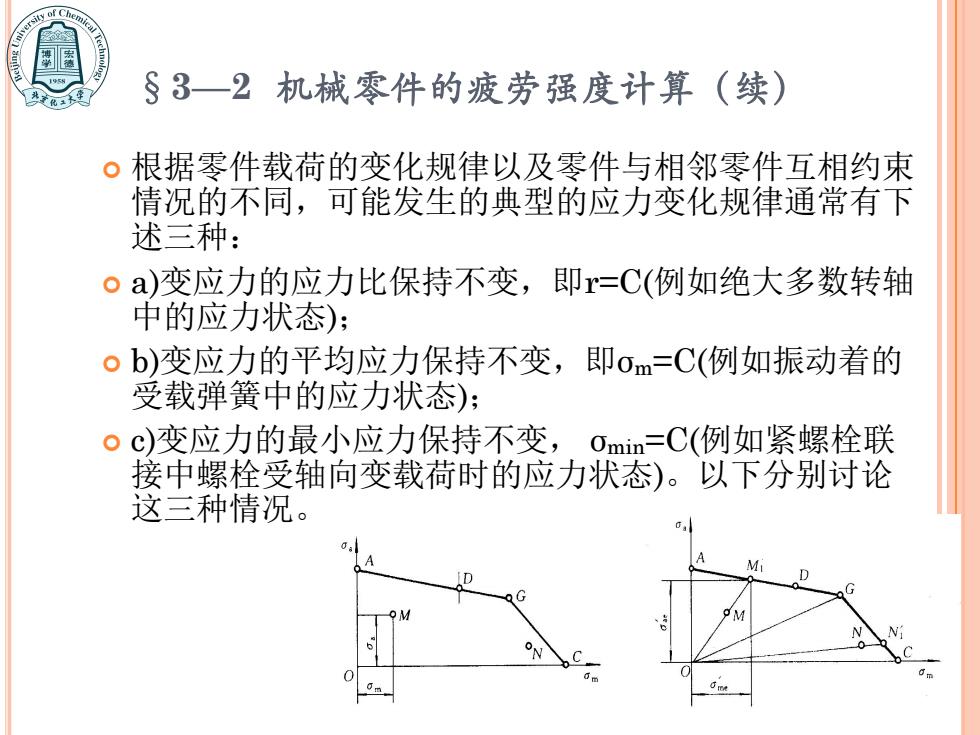
§3一2机械零件的疲劳强度计算（续) 。根据零件载荷的变化规律以及零件与相邻零件互相约束 情况的不同，可能发生的典型的应力变化规律通常有下 述三种： oa)变应力的应力比保持不变，即r=C(例如绝大多数转轴 中的应力状态)： 。b)变应力的平均应力保持不变，即om=C(例如振动着的 受载弹簧中的应力状态)； 。c)变应力的最小应力保持不变，omin=C(例如紧螺栓联 接中螺栓受轴向变载荷时的应力状态)。以下分别讨论 这三种情况。 01 M

 根据零件载荷的变化规律以及零件与相邻零件互相约束 情况的不同，可能发生的典型的应力变化规律通常有下 述三种：  a)变应力的应力比保持不变，即r=C(例如绝大多数转轴 中的应力状态)；  b)变应力的平均应力保持不变，即σm=C(例如振动着的 受载弹簧中的应力状态)；  c)变应力的最小应力保持不变， σmin=C(例如紧螺栓联 接中螺栓受轴向变载荷时的应力状态)。以下分别讨论 这三种情况。 §3—2 机械零件的疲劳强度计算（续）