
sity of C omN=oN。=C 0 以上各式中,m为材料常数,其值由试验来决定。对 于钢材,在弯曲疲劳和拉压疲劳时,m=6一20, N0=(1一10)×106。在初步计算中,钢制零件受弯曲疲 劳时,中等尺寸零件取m=9,N0=5×106;大尺寸零件 取m=9,No=107。 当N大于疲劳曲线转折点D所对应的循环次数ND时, 式(3一3)中的N就取为ND而不再增加(亦即om=o。 0 图3一1中的曲线CD和D以后两段所代表的疲劳通常 统称为高周疲劳,大多数通用机械零件及专用零件的 失效都是由高周疲劳引起的。 OIN =,NoIN=G,KN
以上各式中,m为材料常数,其值由试验来决定。对 于钢材,在弯曲疲劳和拉压疲劳时,m= 6—20, N0=(1—10)×106 。在初步计算中,钢制零件受弯曲疲 劳时,中等尺寸零件取m=9,N0=5×106;大尺寸零件 取m=9,No=107 。 当N大于疲劳曲线转折点D所对应的循环次数ND时, 式(3—3)中的N就取为ND而不再增加(亦即 )。 图3—1中的曲线CD和D以后两段所代表的疲劳通常 统称为高周疲劳,大多数通用机械零件及专用零件的 失效都是由高周疲劳引起的。 rND r N N C m r m rN 0 r N m rN r N0 / N K
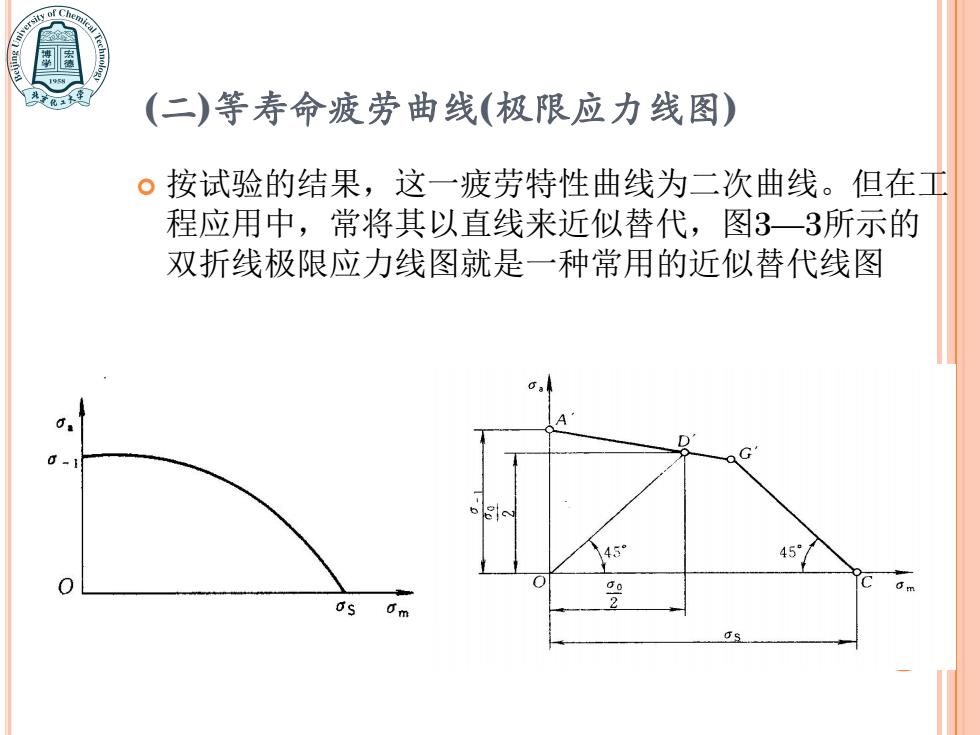
(二)等寿命疲劳曲线(极限应力线图) 。按试验的结果,这一疲劳特性曲线为二次曲线。但在工 程应用中,常将其以直线来近似替代,图3一3所示的 双折线极限应力线图就是一种常用的近似替代线图 6 D 45° 0
(二)等寿命疲劳曲线(极限应力线图) 按试验的结果,这一疲劳特性曲线为二次曲线。但在工 程应用中,常将其以直线来近似替代,图3—3所示的 双折线极限应力线图就是一种常用的近似替代线图

45 。零件材料(试件)的极限应力曲线即为折线A'G'C。材料中发生的应 力如处于OAG,C区域以内,则表示不发生破坏:如在此区域以外, 则表示一定要发生破环;如正好处宇折线上,厕表示工作应万厌况正 好达到极限状态。 。图3一3中直线A'G′的方程可由己知两点坐标A'(0,o.)及D' (oo/2,0/2)求得,即 0.1=0a +0m (3-4) 。直线CG',的方程为 0 0a′+0m′=0g (3-5) 式中oa'、om'为试件受循环弯曲应力时的极限应力幅与极限平均应 为试件受循环弯曲应力时的材料常数,其值由试验及下式决定 。= 2o-1-00(3—6) 00 o根据试验,对碳钢,W。≈0.1~0.2;对合金钢,。≈0.2~0.3
零件材料(试件)的极限应力曲线即为折线A'G'C。材料中发生的应 力如处于OA'G'C区域以内,则表示不发生破坏;如在此区域以外, 则表示一定要发生破坏;如正好处于折线上,则表示工作应力状况正 好达到极限状态。 图3—3中直线A'G'的方程可由已知两点坐标A'(0,σ-1)及D' (σ0/2,σ0/2)求得,即 σ-1=σa '+ψσσm ' (3-4) 直线C G' ,的方程为 σa '+σm '=σs (3—5) 式中σa ' 、σm '为试件受循环弯曲应力时的极限应力幅与极限平均应 力; ψσ为试件受循环弯曲应力时的材料常数,其值由试验及下式决定 (3—6) 根据试验,对碳钢,ψσ ≈0.1~0.2;对合金钢,ψσ ≈ 0.2 ~ 0.3。 0 2 1 0

§3一2机械零件的疲劳强度计算 。由于零件尺寸及几何形状变化、加工质量及强 化因素等的影响,使得零件的疲劳极限要小于 材料试件的疲劳极限。如以弯曲疲劳极限的综 合影响系数K表示材料对称循环弯曲疲劳极限 o.1与零件对称循环弯曲疲劳极限σ.1e的比值,即 Ko=0.1/0.1e (3-7) o当己知K及o时,则 0.1e=0.1/K (3—8)
§3—2 机械零件的疲劳强度计算 由于零件尺寸及几何形状变化、加工质量及强 化因素等的影响,使得零件的疲劳极限要小于 材料试件的疲劳极限。如以弯曲疲劳极限的综 合影响系数Kσ表示材料对称循环弯曲疲劳极限 σ-1与零件对称循环弯曲疲劳极限σ-1e 的比值,即 Kσ =σ-1 /σ-1 e (3—7) 当已知Kσ及σ-1时,则 σ-1e =σ-1 / Kσ (3—8)

sity of C §3一2机械零件的疲劳强度计算(续) 0 在不对称循环时,K是试件的与零件 的极限应力幅的比值。把零件材料的 极限应力线图中的直线A'D'G'按 比例向下移,成为图3一4所示的直线 45 a. ADG,而极限应力曲线的CG′部分, 由于是按照静应力的要求来考虑的, 故不需进行修正。这样一来,零件的 A 极限应力曲线当即由折线AGC表示。 直线AG的方程,由己知两点坐标A(O, o.1/K)及D(o0/2,0o/2K)求得为 图3-4零件的极限应力线图
§3—2 机械零件的疲劳强度计算(续) 在不对称循环时,Kσ是试件的与零件 的极限应力幅的比值。把零件材料的 极限应力线图中的直线A'D'G'按 比例向下移,成为图3—4所示的直线 ADG,而极限应力曲线的CG'部分, 由于是按照静应力的要求来考虑的, 故不需进行修正。这样一来,零件的 极限应力曲线当即由折线 AGC表示。 直线AG的方程,由已知两点坐标A(0, σ-1 / Kσ)及D(σ0/2,σ0 / 2Kσ)求得为