
第二章复变函数的积分 ·§2.1复变函数的积分 。§2.2科希定理 ·§2.3科希公式
1 第二章 复变函数的积分 • §2.1 复变函数的积分 • §2.2 科希定理 • §2.3 科希公式
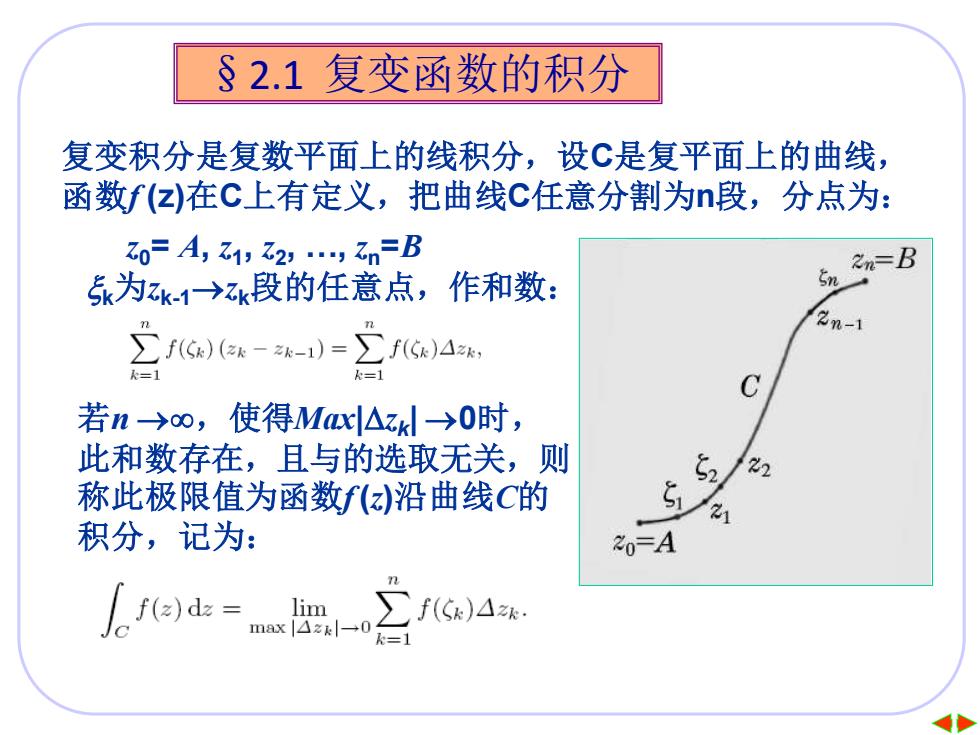
§2.1复变函数的积分 复变积分是复数平面上的线积分,设C是复平面上的曲线, 函数f(z)在C上有定义,把曲线c任意分割为n段,分点为: 30=A,z1,2,乙n=B &n=B k为zk1→k段的任意点,作和数: 2n-1 ∑f)e-6-)=2fG4 k=1 C 若n→oo,使得Ml△zk→0时, 此和数存在,且与的选取无关,则 52 2 称此极限值为函数f()沿曲线C的 21 积分,记为: 0=A 人re)d lim f(Sk)△k. max-0台
2 §2.1 复变函数的积分 复变积分是复数平面上的线积分,设C是复平面上的曲线, 函数f (z)在C上有定义,把曲线C任意分割为n段,分点为: z0= A, z1 , z2 , ., zn =B k为zk-1→zk段的任意点,作和数: 若n →,使得Max|zk | →0时, 此和数存在,且与的选取无关,则 称此极限值为函数f (z)沿曲线C的 积分,记为:

一个复变积分实际上是两个实变线积分的有序组合: f()d=-(u+iv)(dr+id)=(udr-vd)+i(odz+udy) 如果C是分段光滑曲线,f(z)是C上的连续函数,则复变积 分一定存在 复变积分的基本性质: 1、如果积分ie人.人 都存在,则: L[ne)++n)ds+d++h)ds 2、若C=C+C2+.+Cn,则: fed+fe)ds+.+人fe)d=fe)d: 3、fe)d=-f)d其中C表示C的逆向; 4、afe)d=afed, 其中a为常数;
3 一个复变积分实际上是两个实变线积分的有序组合: 如果C是分段光滑曲线,f (z)是C上的连续函数,则复变积 分一定存在. 1、如果积分 都存在,则: 2、若C=C1+C2+.+Cn,则: 3、 其中C-表示C的逆向; 4、 其中a为常数; 复变积分的基本性质:

5、lf(a)ds∫If(a)l川l 6、If(e)d≤M其中M为V在C上的上界,为C的长度. 显然复变积分的数值依赖于:被积函数、端点位置,即积分 的上下限、积分的路径.对于给定一个被积函数,当端点固 定时,不同的积分路径,积分值一般不同 例1.求∫Rez.C为(0沿实轴由0→1,再平行于虚轴1→1+i5 (训)沿虚轴由0→i,再平行于实轴i→1+i,(i训沿直线0→1+i. 解:f(z)=Rez→u=x,v=0. 根据∫cfz)k=c(uc-)+c+u. (训 Re:d:= [rdr- (i0)直线方程为x=y,dx=dy
4 显然复变积分的数值依赖于:被积函数、端点位置,即积分 的上下限、积分的路径.对于给定一个被积函数,当端点固 定时,不同的积分路径,积分值一般不同. 例1. 求 . C为(i) 沿实轴由0→1,再平行于虚轴1 →1+i; (ii) 沿虚轴由0 →i,再平行于实轴i→1+i; (iii) 沿直线0 →1+i. Re C zdz (ii) x y o 1 i (1, )i ( )i ( ) ii ( ) iii 解: f z z ( ) Re = u x v = = , 0. 根据 ( ) ( ) . C C C f z dz udx vdy i vdx udy = − + + (i) (iii)直线方程为x=y,dx=dy. 5 | | | || | ( ) ( ) C C f z dz f z dz 、 6、 | | f z dz Ml ( ) 其中M为|f (z)|在C上的上界,l为C的长度.
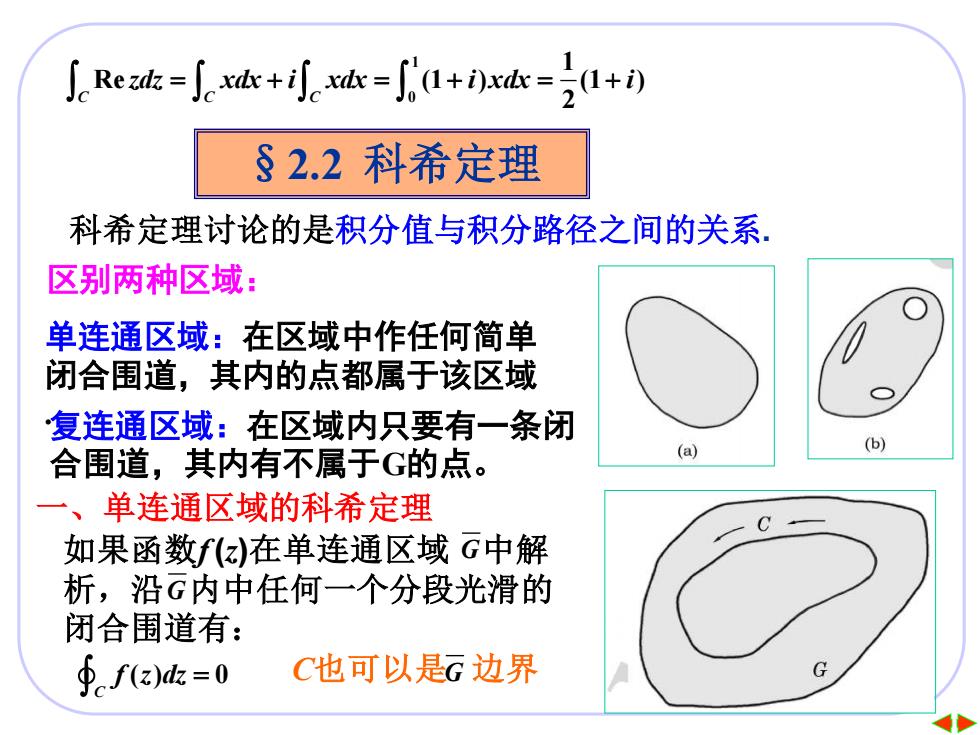
∫Rec=jt+e=ja+0c=+) §2.2科希定理 科希定理讨论的是积分值与积分路径之间的关系. 区别两种区域: 单连通区域:在区域中作任何简单 闭合围道,其内的点都属于该区域 复连通区域:在区域内只要有一条闭 合围道,其内有不属于G的点。 (a) 一、单连通区域的科希定理 如果函数f(z)在单连通区域G中解 析,沿G内中任何一个分段光滑的 闭合围道有: ∮fz)k=0 C也可以是G边界
5 1 0 1 Re (1 ) (1 ) C C C 2 zdz xdx i xdx i xdx i = + = + = + §2.2 科希定理 科希定理讨论的是积分值与积分路径之间的关系. 区别两种区域: 单连通区域:在区域中作任何简单 闭合围道,其内的点都属于该区域 .复连通区域:在区域内只要有一条闭 合围道,其内有不属于G的点。 一、单连通区域的科希定理 G G 如果函数f (z)在单连通区域 中解 析,沿 内中任何一个分段光滑的 闭合围道有: ( ) 0 C f z dz = C也可以是G 边界