
第八章分离变量法 为了把偏微分方程分解成常微分方程,需要把 依赖于多个宗量的未知函数分离成只依赖于 单个宗量的函数的乘积这种称为分离变量法: 分离变量法是解数学物理方程定解问题的一 个重要方法
1 第八章 分离变量法 为了把偏微分方程分解成常微分方程,需要把 依赖于多个宗量的未知函数分离成只依赖于 单个宗量的函数的乘积.这种称为分离变量法. 分离变量法是解数学物理方程定解问题的一 个重要方法

§8.1两端固定的弦的振动 w,-a2u=0 (0<x<L,t>0; 泛定方程 4=p(x,4l=y(c) (0<x<: 初始条件 4e=0,4g=0 (t>0). 边界条件 本征函数与本征值问题是分离变量法的核心,分 离变量法也可称为本征函数法.用分离变量法求 定解问题的解,主要通过如下四项步骤: 2
2 §8.1 两端固定的弦的振动 ( ) ( ) ( ) ( ) ( ) 2 0 0 0 0 0 , 0 ; , 0 ; 0, 0 0 . tt xx t t t x x l u u x l t u x u x x l u u t = = = = − = = = = = 泛定方程 初始条件 边界条件 本征函数与本征值问题是分离变量法的核心,分 离变量法也可称为本征函数法.用分离变量法求 定解问题的解,主要通过如下四项步骤:

44-ad2un=0 0<x<1,t>0): 泛定方程 um=o(x),u=v(x) (0<x<I 初始条件 4e=0,4e=0 (t>0). 边界条件 ()分离变量 两列反向行进的同频率的波形成驻 波。驻波没有波形的传播现象,即 各点振动周期并不依次滞后,它们 按同一方式随时间振动,可以统一 表示为T().但它们的振幅X却随地 点x而异,写成X(x): u(x,t)=X(x)T(t) 自变数x,出现分离 3
3 ( ) ( ) ( ) ( ) ( ) 2 0 0 0 0 0 , 0 ; , 0 ; 0, 0 0 . tt xx t t t x x l u u x l t u x u x x l u u t = = = = − = = = = = 泛定方程 初始条件 边界条件 波腹 波 节 波 节 波 节 波 节 两列反向行进的同频率的波形成驻 波腹 波腹 波腹 波腹 波。驻波没有波形的传播现象,即 各点振动周期并不依次滞后,它们 按同一方式随时间振动,可以统一 表示为T (t). 但它们的振幅X却随地 点x而异, 写成X (x). u x t X x T t ( , ) = ( ) ( ) 自变数x,t出现分离 (1)分离变量

用(x,t)=X(x)T(t)作为试探解的依据: ① 行波在端点间往复反射可能形成驻波,而csin(ot+6)sinl: 就是时空分开的。 ② 如找出一些满足泛定方程和边界条件的驻波,由于泛定方 程和边界条件均是线性的,将这些驻波线性迭加后的解仍 然满足泛定方程和边界条件。如果能确定出迭加系数使之 满足初始条件,就能解决该定解问题。 由泛定方程:,-d2un=0→X(x)T"(d)-aX"(x)T()=0 两边同乘以 T"X" a'XT a27-X =0> 方程左边仅是x的函数,右边仅是的函数,而比,t是独立变量, 只有两边同等于一个常数(-入)时,方程才能成立. 〉X"+1X=0;T"+a2T=0. 4
4 用 u x t X x T t ( , ) = ( ) ( ) 作为试探解的依据: ① 行波在端点间往复反射可能形成驻波,而 就是时空分开的。 c t kx sin sin ( + ) 由泛定方程: 2 0 tt xx u u − = ( ) ( ) ( ) ( ) 2 X x T t X x T t '' '' 0 − = 两边同乘以 2 1 XT 2 '' '' 0 T X T X − = 2 X T '' '' X T = 方程左边仅是x的函数,右边仅是t的函数,而x, t是独立变量, 只有两边同等于一个常数(- )时,方程才能成立. 2 X X T T '' 0; '' 0. + = + = ② 如找出一些满足泛定方程和边界条件的驻波,由于泛定方 程和边界条件均是线性的,将这些驻波线性迭加后的解仍 然满足泛定方程和边界条件。如果能确定出迭加系数使之 满足初始条件,就能解决该定解问题
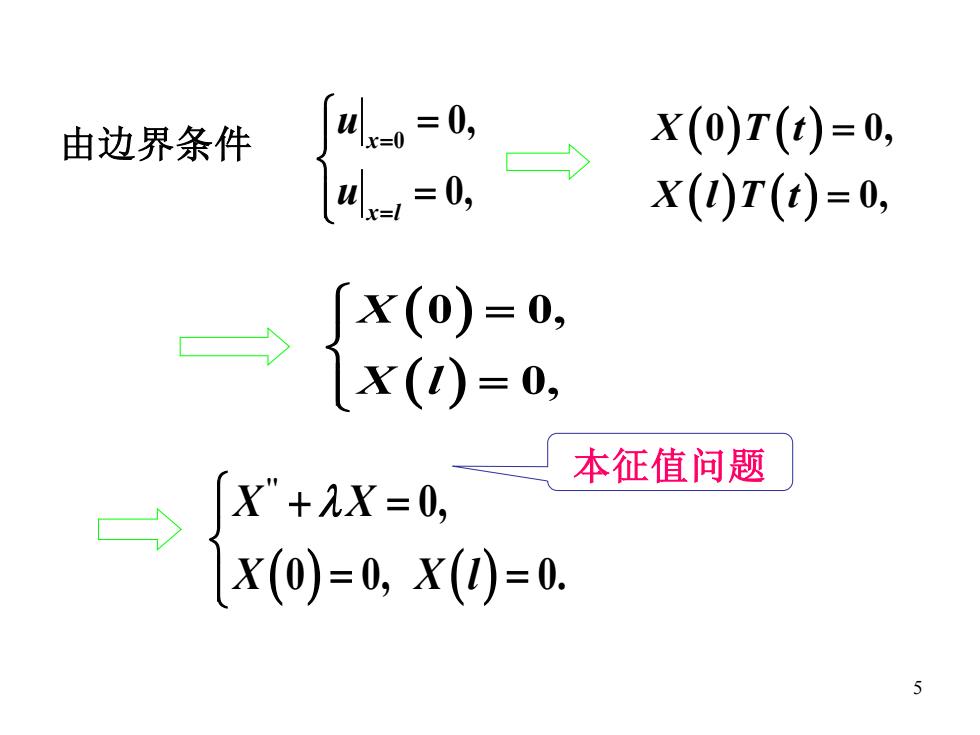
由边界条件 4x=0, X(0)T(t)=0, 4=0, X()T(t)=0, X(0)=0, X()=0, 本征值问题 X"+X=0, X(0)=0,X(0)=0. 5
5 0 0, 0, x x l u u = = = = 由边界条件 ( ) ( ) ( ) ( ) 0 0, 0, X T t X l T t = = ( ) ( ) 0 0, 0, X X l = = ( ) ( ) '' 0, 0 0, 0. X X X X l + = = = 本征值问题