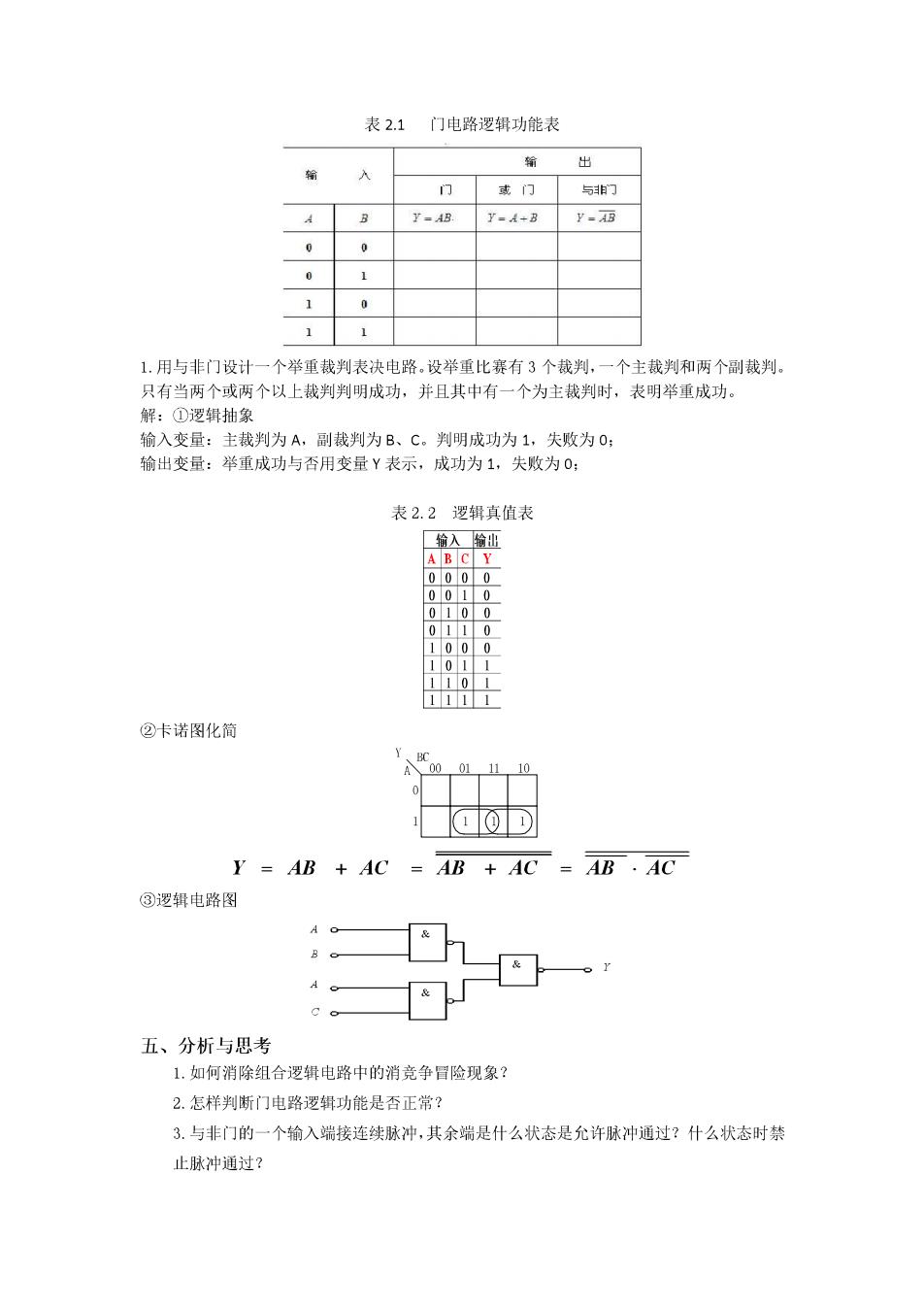
表2.1门电路逻辑功能表 出 入 减门 与门 Y-4-8 1 1.用与非门设计一个举重裁判表决电路。设举重比赛有3个裁判,一个主裁判和两个副裁判。 只有当两个或两个以上裁判判明成功,并且其中有一个为主裁判时,表明举重成功。 解:①逻锅抽象 输入变量:主判为A 副裁判为B、C。判明成功为1,失败为0; 输出变量:举重成功与否用变量Y表示,成功为1,失收为0: 表2.2逻辑真值表 0i00 ②卡诺图化简 CO O1 11 Y=AB+AC=AB+AC=AB·AC ③逻辑电路图 五、分析与思考 1.如何消除组合逻辑电路中的消竞争冒险现象 2.怎样判断门电路逻辑功能是否正常? 3.与非门的一个输入端接连续脉冲,其余端是什么状态是允许脉冲通过?什么状态时禁 止脉冲通过?
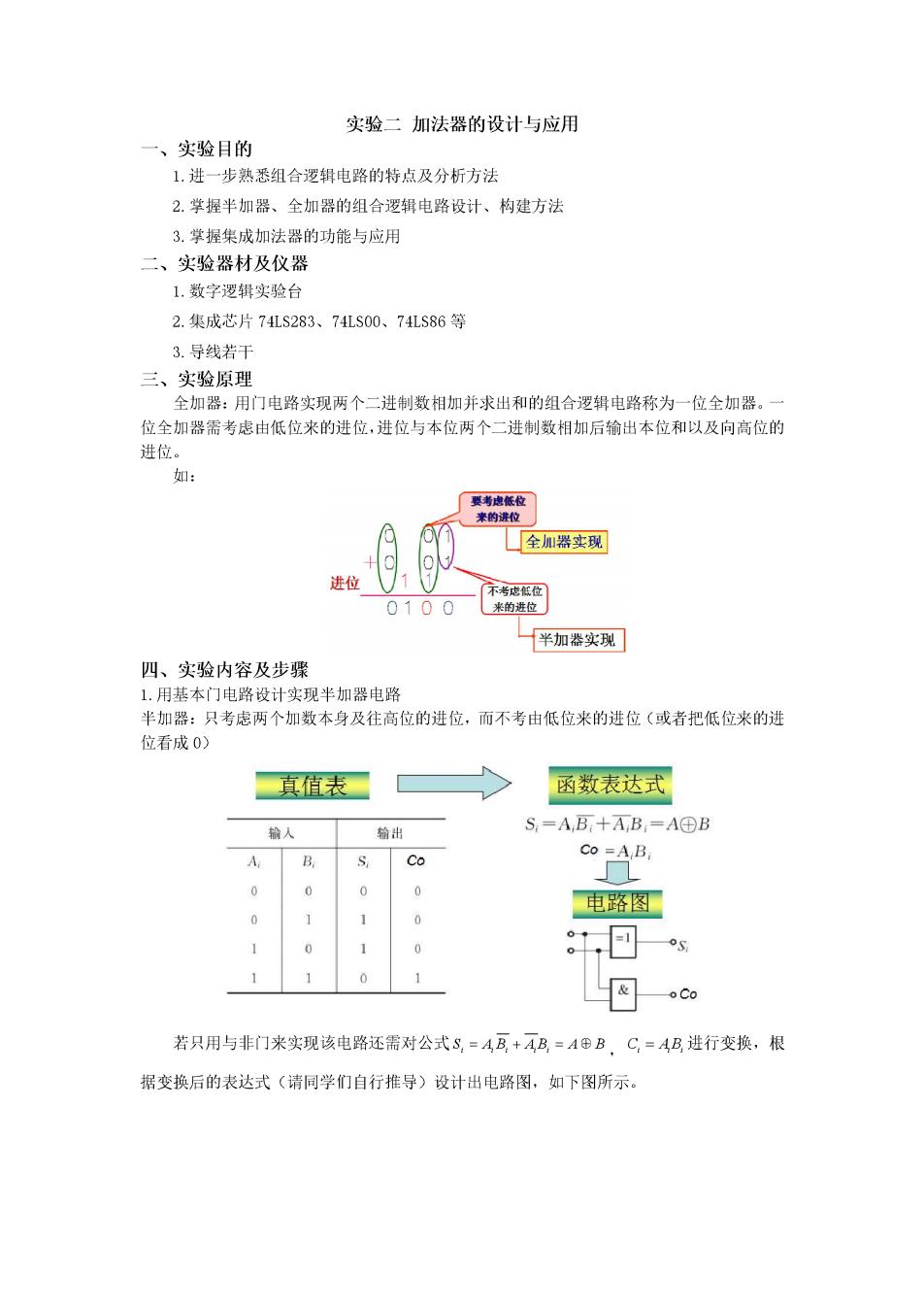
实验二加法器的设计与应用 一、实验目的 1,进一步熟悉组合逻辑电路的特点及分析方法 2.学握半加器、全加器的组合逻辑电路设计、构建方法 3.学握集成加法器的功能与应用 二、实验器材及仪器 1.数字逻辑实验台 2.集成芯片74LS283、74LS00、7LS86等 3.导线若干 三、实验原理 全加器:用门电路实现两个二进制数相加并求出和的组合逻辑电路称为一位全加器。 位全加器需考虑由低位来的进位,进位与本位两个二进制数相加后输出本位和以及向高位的 进位 如 要考虑低位 全器实现 进位 0100 不 半加春实现 四、实验内容及步骤 用基本门电路设计实现半加器电路 半加器:只考虑两个加数本身及往高位的进位,而不考由低位来的进位(或者把低位来的进 位看成0) 真值表 函数表达式 输人 输出 S,=AB,+A,B,=A©B 电路图 0 1可s 1 1 0 1 若只用与非门来实现该电路还需对公式S=4B+AB=A©B,C=AB进行变换,根 据变换后的表达式(请同学们自行推导)设计出电路图,如下图所示
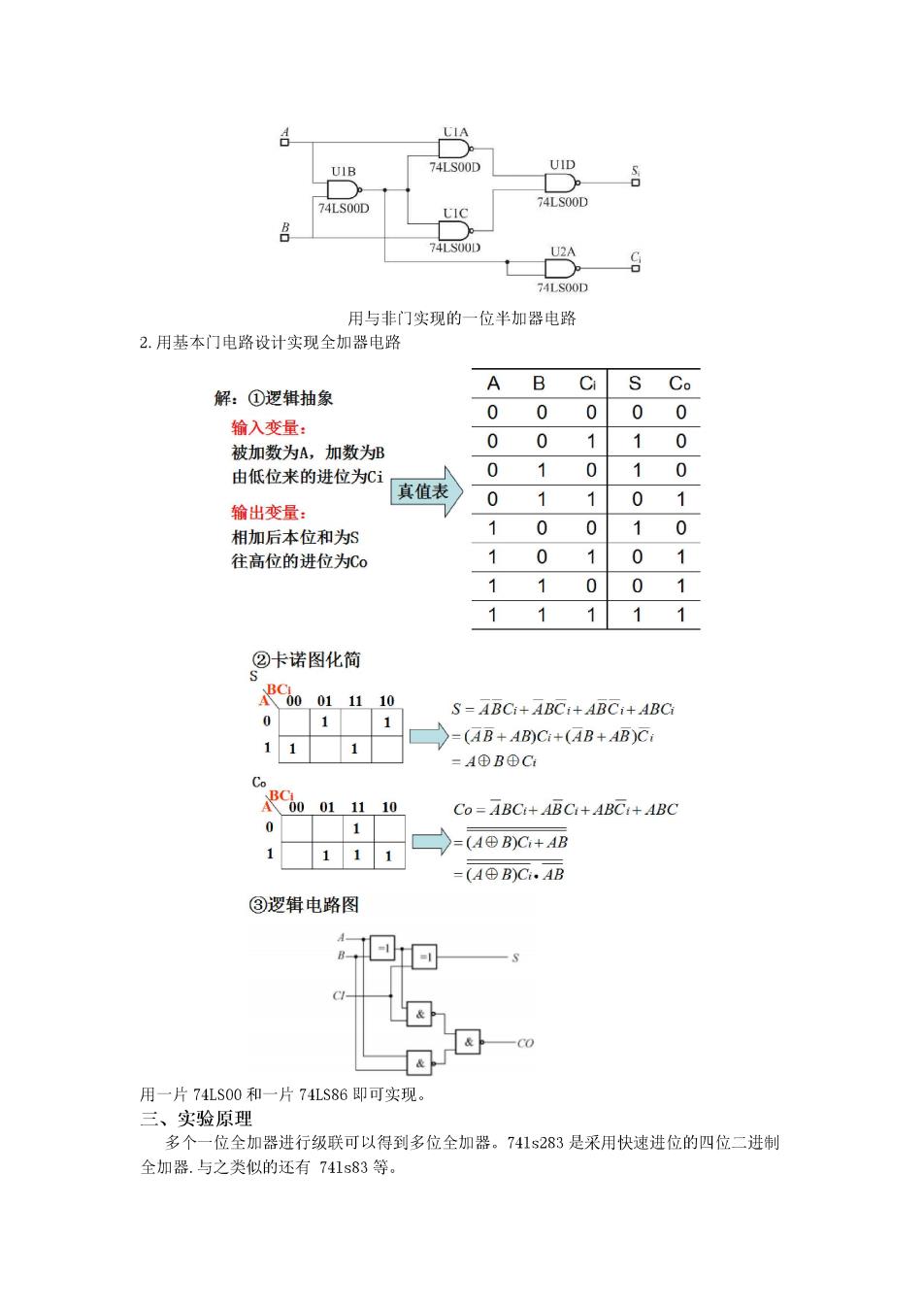
A 74LS00D 74LS00 74LSOOD 用与非门实现的一位半加器电路 2.用基本门电路设计实现全加器电路 解:①逻辑抽象 A B Ci S Co 000 00 输入变量: 被加数为A,加数为 00 1 10 由低位来的进位为Ci 01 0 10 真值表 01 101 输出变量: 相加后本位和於 0 0 10 往高位的进位为C: 0 1 01 1 1 0 01 1 1 1 11 ②卡诺图化简 60011110 S=ABC:+ABC:+ABC+ABC 01 111 -(AB+ABC+(AB+AB)C, =A④BC C001110 Co=ABCi+ABCi+ABCi+ABC 0 =4⊕B)C+AB 1111 (d⊕B)C.AB ③逻辑电路图 —c0 用一片74LS00和一片74LS86即可实现 三、实验原理 多个一位全加器进行级联可以得到多位全加器。7415283是采用快速进位的四位二进制 全加器.与之类似的还有741s83等
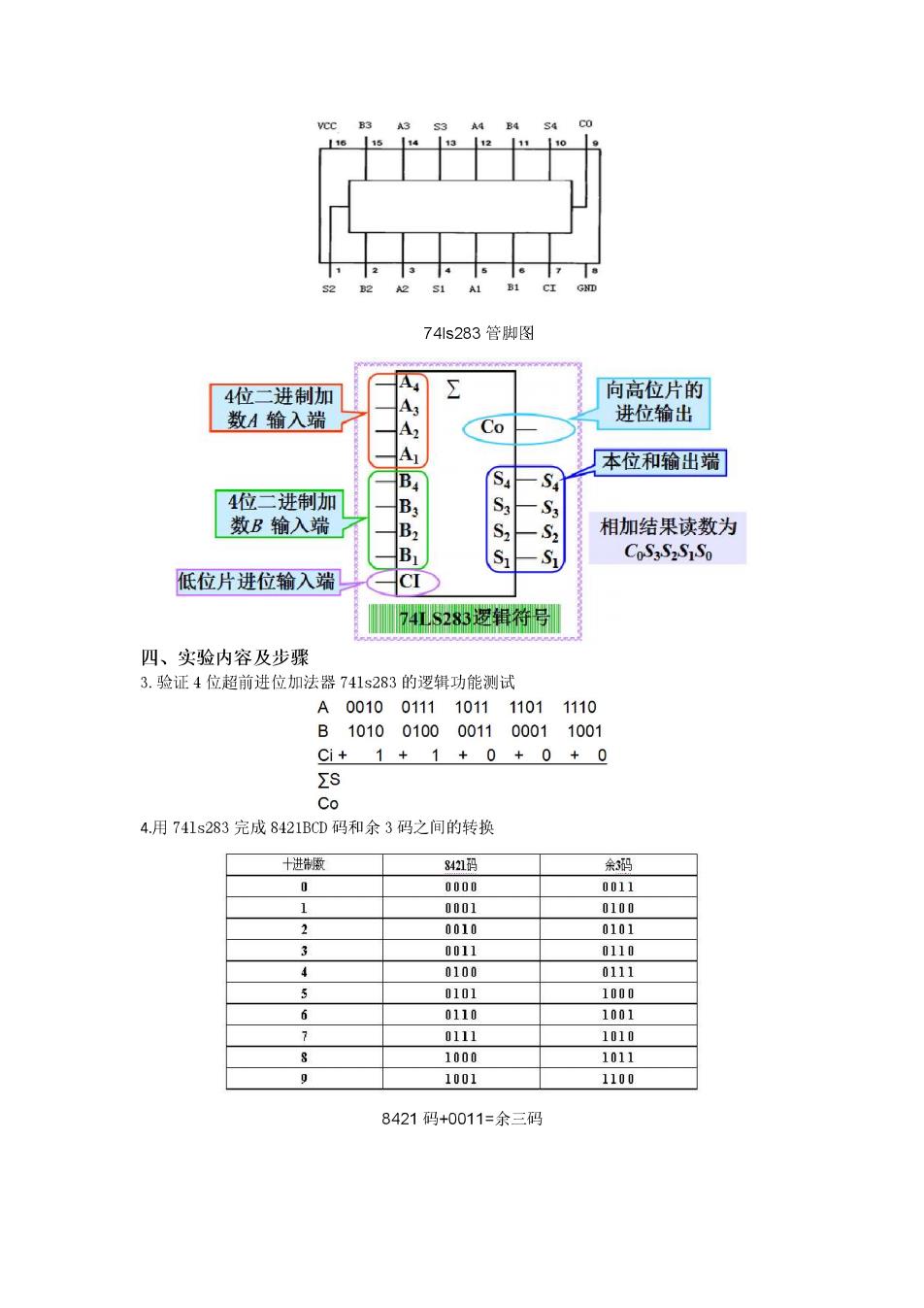
。。 251 741s283管脚图 4位二进制加 向高位片的 数A输入端· Co 进位输出 本位和输出端 S. 4位二进制加 数B输入端 9 B 相加结果读数为 B 5 低位片进位输入端 7415283逻辑符号 四、实验内容及步骤 3.验证4位超前进位加法器741s283的逻辑功能测试 0010 0111 10111101 1110 B 10100100001100011001 Ci+1+1+0+0+0 SS Co 4.用741s283完成8421BCD码和余3码之间的转换 十进 3421码 000 0011 001 001 0110 1001 0111 1010 1000 1011 1001 1100 8421码+0011=余三码

13 Y2 Y1 Yo 余3码 S3 S2 S1 So co 74LS283C A3 A2 A:Ao B3 B2 B Bo 8421BCD码 0011 由74LS283构成的代码转换电路 5.用四位超前进位加法器741s283设计一个加/减运算电路,当M0时,实现加法:当W=1时 实现减法。 对于A-B,可以表示为补码运算式:A+()=A+B+1,B的反码可以用异或门来实现。 这样“A”可以直接输入到一组四位二进制的数,“1”可以直接由最低位进位C!端输入高电 平“1”,从而实现了把减法变成加法。 N厦=(2"-1)-N原 N补-2”-N原;N补-N友1 A-B=A+B-2"=A+BE+1-2” Sa S3 S:So 74LS283 NDA:A:Ao B3 B3 B:Bo 五、分析与思考 1.74S283如何实现级联? 2.如何将余3码转换成BCD码? 3.将实验内容4中的条件改为“当1时,实现加法:当M0时,实现减法”时应该如 何设计电路?