电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第三章 谐振腔理论（1/5）

导波场论 2.5波导的损耗-波导壁的损耗 >例：有耗矩形波导的损耗计算 考虑根据前面分析过程，由导波系统中的波 型耦合，如何计算主模的波导壁损耗？ (y2-r)a,=Zn∑a,∮j0uJJn+「ZrJsJen]dl

导 波 场 论 2.5波导的损耗-波导管壁的损耗  例：有耗矩形波导的损耗计算 考虑根据前面分析过程，由导波系统中的波 型耦合，如何计算主模的波导壁损耗？ 2 2 * ( ) [ ] n n m s ts tn s n zs zn s c         a Z a j J J Z J J dl  

导波场论 根据前面分析，矩形波导中H波和E波的横向电场分别为： Hnm波型： mπ nπx mny .-g 1/2 b cos sin a b ab nπ nπx mπy 0y sin cos a a b E,nmn波型： mπ nπx mπy +s 1/2 cos sin a b 1mπ nπx mπy -a, sin- cos b a b

导 波 场 论 根据前面分析，矩形波导中H波和E波的横向电场分别为： 1/2 2 2 1/2 0 0 cos sin sin cos nm x n m nm y H m n x m y a m n b a b e b a ab n n x m y a a a b                                                     波型： 1/2 2 2 1/2 0 0 cos sin sin cos nm x n m nm y E m n x m y a m n b a b e b a ab m n x m y a b a b                                                      波型：

导波场论 H波的表面电流为（与H相关)： y,x=0 -a,cos-b l/2 1/2 EonCom mπy ab a,cosnπcos tnm jouo nπx a.c0s-,y=0 a nπx -a,cosmπcosa,y=b mπ. mπy sin b b x=0 1/2 EonEom -mπ B y nm ab b cosnπsinb ,X=a j+gj -nπ nπ sin- ,y=0 a a nπ nπx cosmπsin,y=b a a

导 波 场 论 H波的表面电流为（与H相关）： 1/2 2 2 1/2 0 0 0 cos , 0 cosn cos , cos , y 0 cosm cos , y y n m y tnm x x m y a x b n m m y a x a a b ab b J j n x a a n x a b a                                                        1/2 0 0 1/2 2 2 0 sin , 0 cosn sin , sin , y 0 cosm sin , y n m nm znm m m y x b b m m y x a ab b b J n n x n m a a a b n n x b a a                                                             

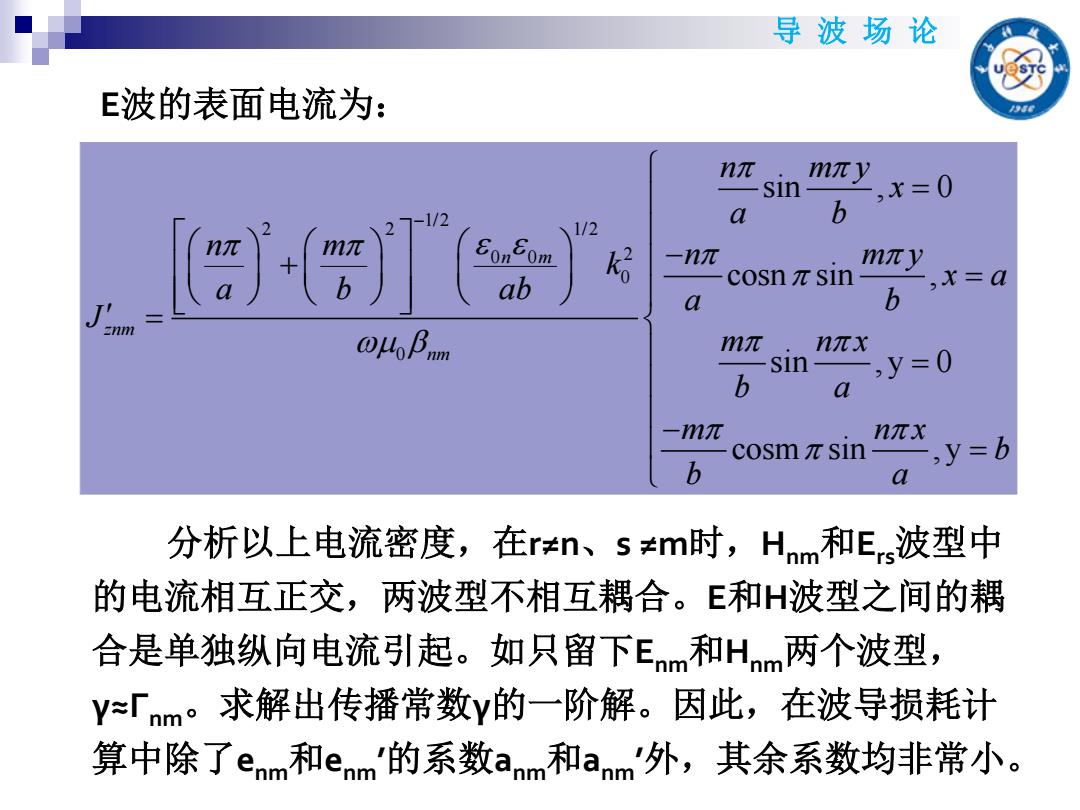
导波场论 E波的表面电流为： nπ miy sin ,x=0 a b 2 1-1/2 1/2 ab k后 -nπ cosnπSln mny ,x=a a b 1mπ nπx sin ,y=0 b a -1mπ nπX coSmπSln ,y=b b a 分析以上电流密度，在rn、sm时，Hnm和Ers波型中 的电流相互正交，两波型不相互耦合。E和H波型之间的耦 合是单独纵向电流引起。如只留下Enm和Hnm两个波型， Y=「nm。求解出传播常数y的一阶解。因此，在波导损耗计 算中除了enm和enm'的系数anm和anm'外，其余系数均非常小

导 波 场 论 E波的表面电流为： 分析以上电流密度，在r≠n、s ≠m时，Hnm和Ers波型中 的电流相互正交，两波型不相互耦合。E和H波型之间的耦 合是单独纵向电流引起。如只留下Enm和Hnm两个波型， γ≈Γnm。求解出传播常数γ的一阶解。因此，在波导损耗计 算中除了enm和enm ’的系数anm和anm ’外，其余系数均非常小。 1/2 2 2 1/2 0 0 2 0 0 sin , 0 cosn sin , sin , y 0 cosm sin , y n m znm nm n m y x a b n m n m y k x a a b ab a b J m n x b a m n x b b a                                                               

导波场论 积分后得到齐次方程： (y+Bi)jouoab +k 2b 2a c.nm ￡0m mnπ nm ab (b-a）am=0 + c.nm c.nm g,是g 若a=b(方波导)，非对角线上的两项等于零，E波和H 波无耦合。 若ab(矩形波导)，行列式等于零，可以求得anm和anm 的解。令行列式等于零，得到两个Y2根： 一个根anm>anm',微扰的Hnm波型 一个根anm<anm',微扰的Enm波型

导 波 场 论 积分后得到齐次方程： 若a=b（方波导），非对角线上的两项等于零，E波和H 波无耦合。 若a≠b（矩形波导），行列式等于零，可以求得anm和anm ’ 的解。令行列式等于零，得到两个γ2根： 一个根anm＞anm ’，微扰的Hnm波型 一个根anm＜anm ’，微扰的Enm波型     2 2 0 2 , 2 2 0 0 0 0 0 2 2 2 2 , 2 , 2 2 0 nm c nm m n m m n nm nm c nm nm c nm j ab b a k Z k mn a b a a k ab n m a b k a b                                                                  2 2 2 2 2 2 2 0 0 2 2 , 0 0 , 0 nm nm nm nm c nm m n m c nm mn n m j ab k b a a b a a k ab Z k a b                                               