导波场论 回顾波导损耗一 壁损耗 e=∑a,e e-ba2&-小ieea 有壁损耗的传播常数 e.e+k2G加-e =0 e.7e.+k2+e-2.e0 无壁损耗的传播常数 (理想良导体时波型) y-ra把,gaan可geAn@l 金属波阻抗 层g陪 Z
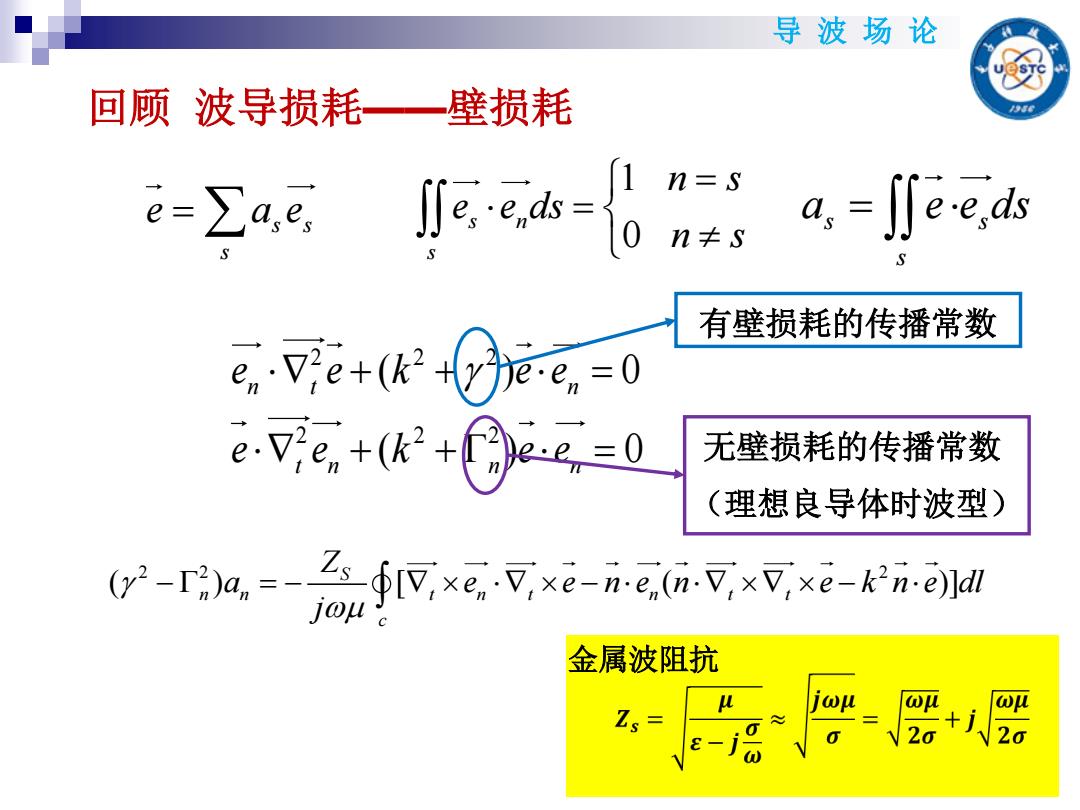
导 波 场 论 回顾 波导损耗——壁损耗 s s s e a e 1 0 s n s n s e e ds n s s s s a e e ds 2 2 2 ( ) [ ( )] S n n t n t n t t c Z a e e n e n e k n e dl j 2 2 2 2 2 2 ( ) 0 ( ) 0 n t n t n n n e e k e e e e k e e 金属波阻抗 有壁损耗的传播常数 无壁损耗的传播常数 (理想良导体时波型)

导波场论 2.5波导的损耗一壁损耗 --aVxc-V.xe.-i-c-VxVx (y2-I')a n=1,2,3.. (y2-)a a, (y2-2)0n a 无限多个线性方程组实际上是无解的。 因为Z很小,所以一般an也很小。只有当所求波的Y接近于 无耗波导的某个波型工n’这个an才比较大。 若Y=Y下n,即求解的也为接近于理想状态下传播常数的 “微扰”波型时,只考虑en就可以得到一级近似解
导 波 场 论 无限多个线性方程组实际上是无解的。 因为Zm很小,所以一般an也很小。只有当所求波的γ接近于 无耗波导的某个波型Γn,这个an才比较大。 若γ=γn=Γn ,即求解的也为接近于理想状态下传播常数的 “微扰”波型时,只考虑en就可以得到一级近似解。 2 2 2 ( ) [ ( )] 1,2,3...... m n n s t n t s n t t s s s Z a a e e n e n e k n e dl j n 2 2 1 1 1 2 2 2 2 2 2 2 ( ) ( ) ( ) n n n a a a a a a 2.5 波导的损耗—壁损耗

导波场论 进一步简化 -ra-Σ可可 -k'n-e,)ldl n=1,2,3.. 可,×en.可,×e,=(-jouh.)-(-jouh)=-w2u2hnh,=-o2u2jmJ 7,×en=-j@uh-n 取电场为实数矢量 则磁场必然为虚数,电流也为虚数 7×en7,xe,=o22jwJd n.可,x7,xe,=nVx(-jouh)=-joun.可,×h 可,×e,=-jouh n.可,×7,×e,=k2n-e,+jor,J7,×h、=j0se,+T,i×h
导 波 场 论 进一步简化 t n t s e e 2 2 * ts t n t s tn e e J J 取电场为实数矢量 则磁场必然为虚数,电流也为虚数 t t s n e t zs s s z s h j e i h 2 t t s s s zs n e k n e j J 2 2 2 ( ) [ ( )] 1,2,3...... m n n s t n t s n t t s s s Z a a e e n e n e k n e dl j n t s zs e j h ( ) t zs t zs n j h j n h t n zn e j h 2 2 2 2 ( ) ( ) tn zn zs zn zs ts j h j h h h J J

导波场论 同时 n.e=ZJm 将刚才的几个式子代入求解a的方程,得: -1g=2aor文反2e1r,不-agh Q 0-ra=z∑a.SU@yJ.7+r②Jm n=1,2,3.. :「n0l 对于E波:乙。=-j2 对H波:Zn=-jou/Tm
导 波 场 论 n n zn 同时 n e Z J 2 2 2 2 * 2 2 ( ) [ ( )] m n n s ts tn n zn s s zs s s c Z a a J J Z J k n e j J k n e ds j 将刚才的几个式子代入求解an的方程,得: 对于E波: 2 n Z j n k 2 2 * ( ) [ ] 1,2,3...... n n m s ts tn s n zs zn s c a Z a j J J Z J J dl n / 对H 波: Z j n n

导波场论 (gr2-r)an=Zm∑a,∮[jouJ+「ZJJn]dl 讨论上式 只出现了无耗波导中各波导的壁电流。 当两个波型壁电流正交时,求解a的方程中正交的波型的 展开系数a.便不出现,这说明两个波型不互相耦合。 对于有耗系统,我们仅求解与无耗波型a接近的微扰波型, 而其他a则很小可以忽略。这样无限的方程数,就变成了有限 的方程组了。 求得与工接近的微扰波型 即可求得若干个Y及对应的展开系数
导 波 场 论 只出现了无耗波导中各波导的壁电流。 当两个波型壁电流正交时,求解an的方程中正交的波型的 展开系数as便不出现,这说明两个波型不互相耦合。 2 2 * ( ) [ ] n n m s ts tn s n zs zn s c a Z a j J J Z J J dl 对于有耗系统,我们仅求解与无耗波型an接近的微扰波型, 而其他an则很小可以忽略。这样无限的方程数,就变成了有限 的方程组了。 求得与Γn接近的微扰波型 即可求得若干个γ及对应的展开系数 讨论上式