
2021/9/25 应力场强度因子和平面断裂韧性 ·求K的关键在于求Y。求不同条件下的Y为断裂力学的内容, Y可通过试验得到。 Y=[1.93-3.07(e/w)+14.5(c/w)2-25.07(e/w) +25.8(c/W)门(三点弯,5w=4) 应力场强度因子和平面断裂韧性 ·经典强度理论,设计构件时 g≤[o] [o]=oh或n8 其中σ为断裂强度,σ为屈服强度,n为安全系数 ·上述设计方法不能防止低应力下的脆性断裂。 ·根据断裂力学,采用一个新的表征材料待征的临界值一断 裂韧性,它也是一个材料常数,即应力场强度因子小于或 等于材料的断裂韧性K。 K,=Ya√c≤Ke 11
2021/9/25 11 • 求KI 的关键在于求Y。求不同条件下的Y为断裂力学的内容, Y可通过试验得到。 (三点弯,S/W=4) 应力场强度因子和平面断裂韧性 • 经典强度理论,设计构件时 其中f 为断裂强度, ys为屈服强度,n为安全系数 • 上述设计方法不能防止低应力下的脆性断裂。 • 根据断裂力学,采用一个新的表征材料待征的临界值—断 裂韧性,它也是一个材料常数,即应力场强度因子小于或 等于材料的断裂韧性KIc 应力场强度因子和平面断裂韧性

2021/9/25 应力场强度因子和平面断裂韧性 ·一种构件,使用应力1.3GPa,可从下面两种材料选,判断 一下是否可以安全使用 甲钢:n=1.95GPa,K1,=45wPa·m 乙钢:0m=1.56GPa,K1.=75MPa,m ·经典强度理论,甲钢安全系数大,更为安全 甲幅的安金系数:。-号-士8-15 乙期的安全系数:-8-12 应力场强度因子和平面断裂韧性 最大 45×10 乙制的新裂位河16G 从断裂力学判断,虽然甲钢具有较高的屈服强度,但是不 安全的。 12
2021/9/25 12 • 一种构件,使用应力1.3GPa,可从下面两种材料选,判断 一下是否可以安全使用 • 经典强度理论,甲钢安全系数大,更为安全 应力场强度因子和平面断裂韧性 • 根据断裂力学的观点,可根据断裂韧性计算断裂应力。假 设Y=1.5,最大裂纹尺寸1 mm • 从断裂力学判断,虽然甲钢具有较高的屈服强度,但是不 安全的。 应力场强度因子和平面断裂韧性
2021/9/25 应力场强度因子和平面断裂韧性 ·形成裂纹时释放的弹性能 《平面应力状态 ·应变能释放率或裂纹扩展力 ·临界状态时 G.-T0 K 会-嘉4= =管(平面应力状态) K1:=√2E(平面应力状态) ·同样得到平面应变状态 /26 ·飞为材料参数,反映了阻止裂纹扩展的能力 应力场强度因子和平面断裂韧性 ·最终炎终来的 ·利用不同切口深度(W)的梁,进行弯曲 绕铁裤力F与试件变形6的关系曲 tc/wj-02 C=6/E 表时的力 则有 「m,-受-专0 ·裂纹扩展动力为 c-贸.-器.=品品 图2多不同相对切口深度下 的柔度量测曲线 13
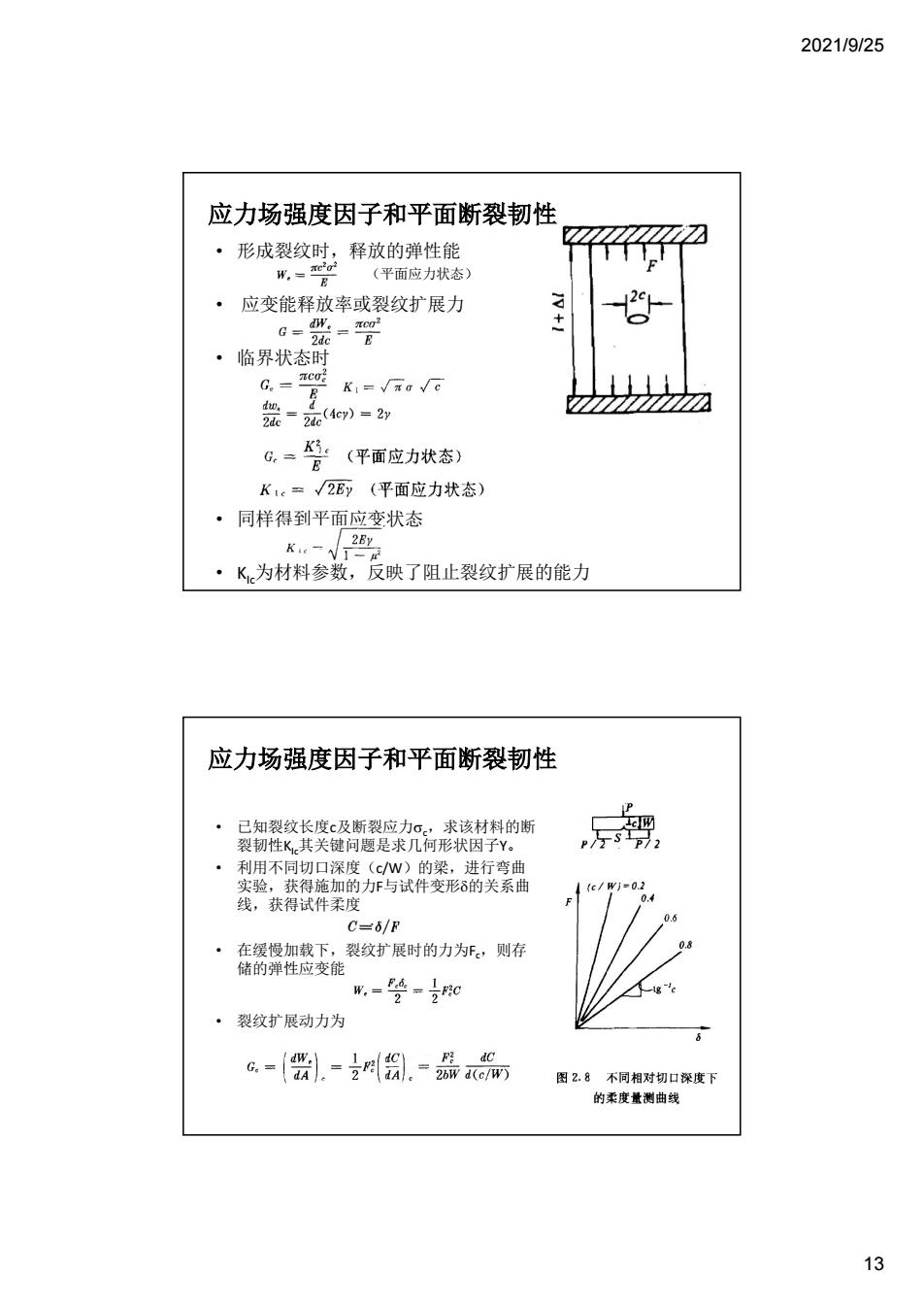
2021/9/25 13 • 形成裂纹时,释放的弹性能 • 应变能释放率或裂纹扩展力 • 临界状态时 • 同样得到平面应变状态 • KIc为材料参数,反映了阻止裂纹扩展的能力 (平面应力状态) 应力场强度因子和平面断裂韧性 • 已知裂纹长度c及断裂应力c ,求该材料的断 裂韧性KIc其关键问题是求几何形状因子Y。 • 利用不同切口深度(c/W)的梁,进行弯曲 实验,获得施加的力F与试件变形的关系曲 线,获得试件柔度 • 在缓慢加载下,裂纹扩展时的力为Fc ,则存 储的弹性应变能 • 裂纹扩展动力为 应力场强度因子和平面断裂韧性

2021/9/25 应力场强度因子和平面断裂韧性 ·eM可通过报合CeW自线 ·我们已经推导出平面应变状态 合适花内处直线 0.-413. ·根据下述关系 . K= 的的亦立 K3.=yrac=Y2w·(c/w) ·进一步获得Y与cw的关系规律。 图29c-(ew)曲线 agwacn-roireln 应力场强度因子和平面断裂韧性 上在裂纹前沿附近,由于高度 小度 线弹性的。因此, 为了确地 小区域的大小限制在 围之内 主要的措施包括: 笈馨 定的 寸以 定的要求 14
2021/9/25 14 • dC/d(c/W)可通过拟合C-c/W曲线 获得。 • 我们已经推导出平面应变状态 • 根据下述关系 • 进一步获得Y与c/W的关系规律。 应力场强度因子和平面断裂韧性 2 2 2 2 ( / ) (1 ) ( / ) c c EF dC Y W c W bW d c W • 上面对断裂判据的计算,是由 线弹性力学推导出来的。实际 上在裂纹前沿附近,由于高度 的应力集中,临近临界状态之 前就已出现小区域的塑性形变, 从而使此区城内的应力状态发 生变化。如果此区域的大小与 原有裂纹长度等尺寸相差不大, 则很难将这种应力状态归结为 线弹性的。因此,为了准确地 引用由线弹性力学计算出的断 裂判据,必须将可能出现的塑 性小区域的大小限制在一定范 围之内。主要的措施包括:裂 纹长度必须超过一定的尺寸以 及试样尺寸有一定的要求。 应力场强度因子和平面断裂韧性

2021/9/25 应力场强度因子和平面断裂韧性 ·根据Irwin的计算结果,裂纹附 近的应力与r和0有关,当0=0时 ·当=o时,材料达到屈服应力 计算为 n ·对于平面应变状态,实际屈服 图210裂纹尖端的塑作变形区 应力会高一些 -2万=12} 应力场强度因子和平面断裂韧性 6% 图2.11不同试样应力场的近似解与精确解的相对误产 ·⊥.F.Knott计算裂纹附近c,的精确解 9(r,9)=C1f1(0) +caf:(0)+ofs (0)in+cf(0)r 并计算,- ,获得。 。×100%随/变化的曲线. 15
2021/9/25 15 • 根据Irwin的计算结果,裂纹附 近的应力与r和有关,当=0时 • 当r=r0 时,材料达到屈服应力 y=ys,对于r<r0 的区域为塑性 变形区,其应力约为ys 。r0 可 计算为 • 对于平面应变状态,实际屈服 应力会高一些 应力场强度因子和平面断裂韧性 • J. F. Knott计算裂纹附近y 的精确解 并计算 ,获得 随r/c变化的曲线。 应力场强度因子和平面断裂韧性