
2021/9/25 无机材料的脆性断裂和强度 脆性断裂现象 ·在外力作用下,无机材料首先出现可恢复的弹性形变】 ·在足够大的剪应力作用 美荣籍淡致的茶奖影姿藏为材料的转性形变,这两种形变 ·当材料长期受载,尤其在高温环境中受载,上述塑性形变 材料的蠕变 产生应力 星2器
2021/9/25 1 无机材料的脆性断裂和强度 • 在外力作用下,无机材料首先出现可恢复的弹性形变。 • 在足够大的剪应力作用下(或环境温度较高时),材料中的 晶体部分将选择最易滑移的系统,出现品较内部的位错滑 移,宏观上表现为材料的塑性形变;无机材料中的晶界非 晶相,以及玻璃、有机高分子材料等非晶态材料,则会产 生粘性流动,宏观上表现为材料的粘性形变。这两种形变 为不可恢复的永久形变。 • 当材料长期受载,尤其在高温环境中受载,上述塑性形变 及粘性形变随时间而具有不同的速率,这就是材料的蠕变。 蠕变的后期或是蠕变终止;或是导致蠕变断裂。 • 在外力作用下,在一些地方(比如缺陷或裂纹)产生应力 集中,超过材料的临界拉应力值,将会产生裂纹或缺陷的 扩展,导致脆性断裂。此时平均剪应力尚小于临界值,不 足以产生明显的塑性变形或粘性流动。 脆性断裂现象

2021/9/25 脆性断裂现象 ·餐纹腐高發料务按等林整费曼杂器 强度)。 ·突发性断裂(瞬时断裂):在较快速率持续增加的应力下发生 断裂。在临界状态下,断裂源处的裂纹尖端所受的横向拉应力 正好等于结合强度时,裂纹产生突发性扩展。 一旦扩展,引起 樱界密动理外宪失录致裂纹的加速扩展,出现突发性断裂, ·延迟性断裂(或疲劳断裂):在缓慢速率持续增加的应力,或 理论结合强度 ·固体材料断裂强度理论上可达到的最高值。 ·将预案子间结合力σ与原子间的距离X近似为正弦关系: =Xn2坠 ·将材料拉断时,产生两个新表面,因此使单位面积的原子 平面分开所作的功应等于产生两个单位面积的新表面所需 的表面能.材料才能断裂。此时,分开单位面积原子平面 所作的功为: -∫如2婴4 -[-织]-g 2
2021/9/25 2 • 裂纹的存在及其扩展行为,决定了材料抵抗断裂的能力。断裂 时.材料的实际平均应力尚低于材料的结合强度(或称理论结合 强度)。 • 突发性断裂(瞬时断裂):在较快速率持续增加的应力下发生 断裂。在临界状态下,断裂源处的裂纹尖端所受的横向拉应力 正好等于结合强度时,裂纹产生突发性扩展。一旦扩展,引起 周围应力的再分配,导致裂纹的加速扩展,出现突发性断裂, 这种断裂往往并无先兆。 • 延迟性断裂(或疲劳断裂):在缓慢速率持续增加的应力,或 承受恒定应力,或循环应力经过一段事件后发生的断裂。有时 裂纹尖端处的横向拉应力尚不足以引起扩展,但在长期受应力 的情况下,待别是同时处于高温环境中或特殊的环境侵蚀时, 如存在O2 ,H2 ,S02 ,H2 0(汽)等的情况下时,会出现裂纹的缓慢 生长,甚至导致一些材料(比如金属和玻璃)易出现缓慢开裂。 脆性断裂现象 • 固体材料断裂强度理论上可达到的最高值。 • 将预案子间结合力与原子间的距离X近似为正弦关系: • 将材料拉断时,产生两个新表面,因此使单位面积的原子 平面分开所作的功应等于产生两个单位面积的新表面所需 的表面能.材料才能断裂。此时,分开单位面积原子平面 所作的功为: 理论结合强度

2021/9/25 理论结合强度 ·形成的表面的表面能为y,则v=2y 9- -婴 ·在平衡位置附近 0=8e=8 ·将上面最后的三个关系式代入 a-X sin 2ax ·最后得到 E为弹性模量,a为晶格常数。 理论结合强度 ·通常其况下,y约为a/100,所以理论结合强度 0a=0 ·实际材料中只有一些极细的纤维和晶须其强度接近理论强 度值。例如熔融石英纤维的强度约为4,碳化硅晶须强 度约为/23,氧化铝晶须强度为/33。尺寸较大的材料的 实际强度比理论值低得多,约为E/100-E/1000。 实际材料的强度总在一定范围内波动,即使是用同样材料 套相灵的餐树议产的试桥,莲度值他有流动。一校试行 ·主要原因实际材料中存在着裂纹和缺陷-Griffith微裂纹理 论,脆性断裂的理论基础。 3
2021/9/25 3 • 形成的表面的表面能为,则v=2 • 在平衡位置附近 • 将上面最后的三个关系式代入 • 最后得到 E为弹性模量,a为晶格常数。 理论结合强度 • 通常其况下,约为aE/100,所以理论结合强度 • 实际材料中只有一些极细的纤维和晶须其强度接近理论强 度值。例如熔融石英纤维的强度约为E/4,碳化硅晶须强 度约为E/23,氧化铝晶须强度为E/33。尺寸较大的材料的 实际强度比理论值低得多,约为E/100-E/1000。 • 实际材料的强度总在一定范围内波动,即使是用同样材料 在相同的条件下制成的试件,强度值也有波动。一般试件 尺寸大.实测强度低。 • 主要原因实际材料中存在着裂纹和缺陷—Griffith微裂纹理 论,脆性断裂的理论基础。 理论结合强度
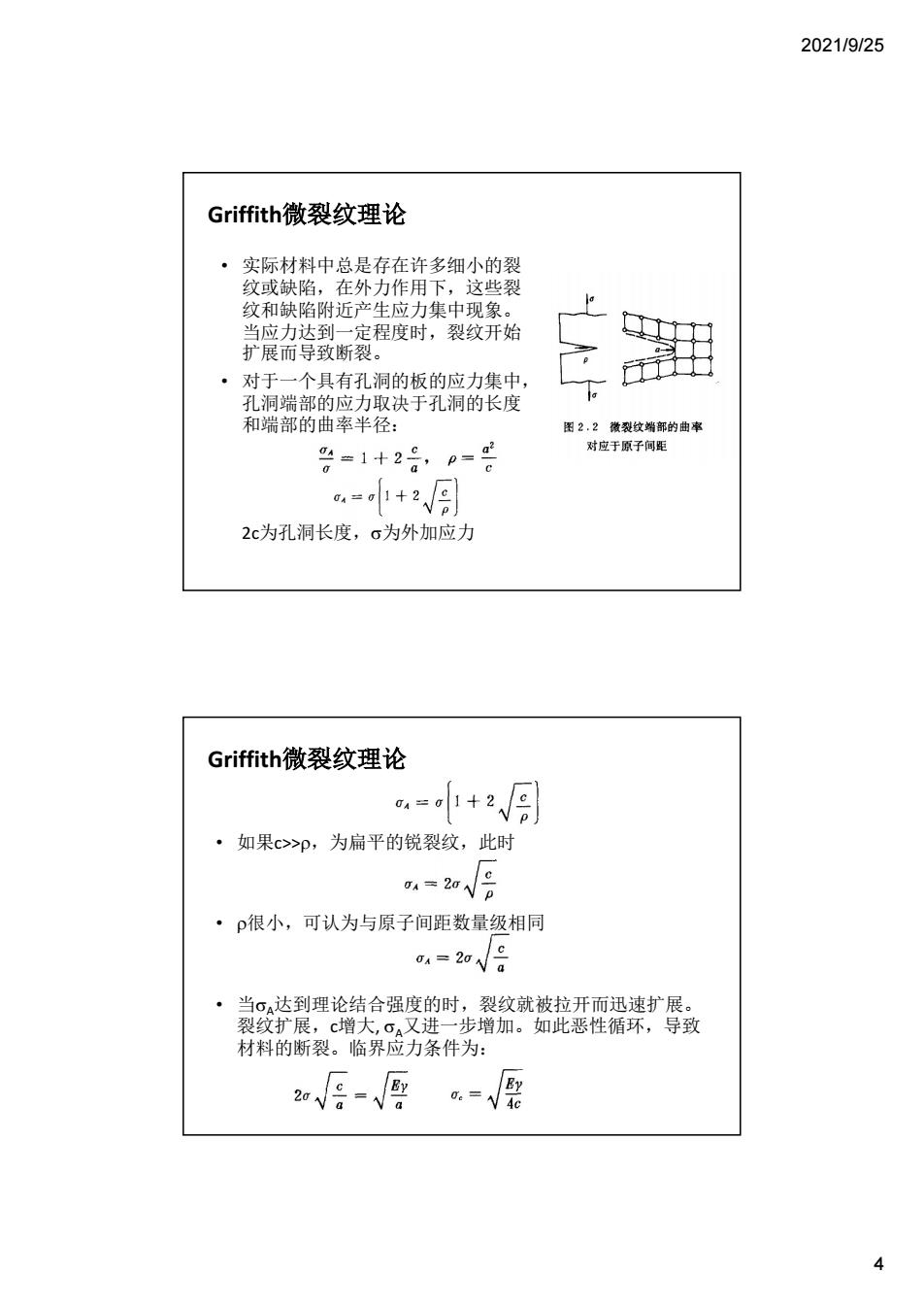
2021/9/25 Griffith微裂纹理论 ·实际材料中总是存在许多细小的裂 纹或缺陷,在外力作用下,这些裂 纹和缺陷附近产生应力集中现象。 肖应力达到一定程度时,裂纹开始 扩展而导致断裂。 ·对于一个具有孔洞的板的应力集中, 孔洞端部的应力取决于孔洞的长度 和端部的曲率半径: 图22徽裂纹端部的曲率 g=1+28,p-日 对应于原子闻至 “-小+月 2c为孔洞长度,。为外加应力 Griffith微裂纹理论 =+月 ·如果c>p,为扁平的锐裂纹,此时 -a月 ·p很小,可认为与原子间距数量级相同 =20√ 材料的裂临险方条件为: 如月-s-√ 4
2021/9/25 4 • 实际材料中总是存在许多细小的裂 纹或缺陷,在外力作用下,这些裂 纹和缺陷附近产生应力集中现象。 当应力达到一定程度时,裂纹开始 扩展而导致断裂。 • 对于一个具有孔洞的板的应力集中, 孔洞端部的应力取决于孔洞的长度 和端部的曲率半径: 2c为孔洞长度,为外加应力 Griffith微裂纹理论 • 如果c>>,为扁平的锐裂纹,此时 • 很小,可认为与原子间距数量级相同 • 当A 达到理论结合强度的时,裂纹就被拉开而迅速扩展。 裂纹扩展,c增大, A 又进一步增加。如此恶性循环,导致 材料的断裂。临界应力条件为: Griffith微裂纹理论

2021/9/25 Griffith微裂纹理论 ·从能量角度而言,物体内储存的弹 性应变能大于裂纹开裂形成的两个 新表面所需的表面能,裂纹发生 展,反之,裂纹不扩展 将以单位长度的薄板拉到+A并固 定,储存的弹性能为 长度为性 能变为 W2=1/2(F-F)·M ·弹性能降低了 We=W4-wa=1/2·M 可用于裂纹的扩展 图23裂纹扩微饰界条件的导出 Griffith微裂纹理论 ·对于薄板(平面应力状态) W,= 厚板(平面应变状态) 所=1-内密 ·产生长度为2c,厚度为1的新的断面所需表面能为 W,=4cy ·会<,裂纹不扩展:会>会时,裂纹扩展:临界状态 会袅 5
2021/9/25 5 • 从能量角度而言,物体内储存的弹 性应变能大于裂纹开裂形成的两个 新表面所需的表面能,裂纹发生扩 展,反之,裂纹不扩展 • 将以单位长度的薄板拉到l+l并固 定,储存的弹性能为 • 割出长度为2c的裂纹,储存的弹性 能变为 • 弹性能降低了 可用于裂纹的扩展 Griffith微裂纹理论 • 对于薄板(平面应力状态), 厚板(平面应变状态) • 产生长度为2c,厚度为1的新的断面所需表面能为 • 时,裂纹不扩展; 时,裂纹扩展;临界状态 Griffith微裂纹理论