兰州交通大学：《数控技术及编程》课程教学资源（教案讲义）06

数控技术及应用教案及讲稿 上部分：数控技术及编程 第六讲 一、备课教案 适用专业机械设计制造及其自动化讲次 上课 第六讲时间 年月日节 第二章计算机数控系统 第二节计算机数控系统的基本原理 教 五。插补原理 内容 4.数字增量插补（时间标量插补） 解数字增量插补（时间标量 (3)圆孤插补算法 补 中圆弧插补算法 六、位置控制原理 理解位置控制原理 要 七、加减速控制 1.前加减速控制 了解前、后加减速控制的概念及 2.后加减速控制 经别：理解、后 教学实施手段 效果记录 数字增量插补（时间标量插补）中 课堂讲授 √ 前、后加减速控制的概念及两者的 课堂讨论 点 区别： 现场示教 前、后加减速控制算法。 小结讲评 难 数字增量插补（时间标量插补）中 其它 位置控制原理 前、后加减速控制算法。 教具 CAI,黑板 推预 陈德道主编数控技术及应用北京 荐复 参习 国防工业出版社，2009 学 考 董玉红主编机床数控技术.哈尔滨 书务 哈尔滨工业大学出版社2003 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 1 第六讲 一、备课教案 适用专业 机械设计制造及其自动化 讲次 第六讲 上课 时间 年 月 日 节 教 学 内 容 提 纲 及 要 求 第二章 计算机数控系统 第二节 计算机数控系统的基本原理 五．插补原理 4．数字增量插补（时间标量插补） 理解数字增量插补（时间标量插 补）中圆弧插补算法 （3）圆弧插补算法 六、位置控制原理 理解位置控制原理 七、加减速控制 1．前加减速控制 了解前、后加减速控制的概念及 两者的区别；理解前、后加减速 2．后加减速控制 控制算法 重 点 数字增量插补（时间标量插补）中 圆弧插补算法； 位置控制原理； 前、后加减速控制的概念及两者的 区别； 前、后加减速控制算法。 教学实施手段 效果记录 课堂讲授 √ 课堂讨论 √ 现场示教 小结讲评 难 点 数字增量插补（时间标量插补）中 圆弧插补算法； 位置控制原理； 前、后加减速控制算法。 其 它 教具 CAI，黑板 推 预 荐 复 参 习 考 任 书 务 陈德道主编.数控技术及应用.北京: 国防工业出版社,2009 董玉红主编.机床数控技术.哈尔滨: 哈尔滨工业大学出版社,2003 教 学 后 记

数控技术及应用教案及讲稿 上部分：数控技术及编程 二、讲稿 第二章计算机数控系统 第二节计算机数控系统的基本原理 3.圆弧插补算法 采用时间分割法进行圆弧插补的基本方法是用内接弦线逼近圆弧。只要在插补过程 中根据半径合理选用进给速度下，就可以使逼近精度满足要求。 同直线插补一样，在设计 弧插补程序时，为] 简化程序设计，通常将插补计算坐 标系的原点选在被插补圆弧的圆心上，如图所示，以第一象限顺圆插补(G02)为例讨 论圆弧插补原理。图中P(x,y,)为圆上某一插补点A,P(x,y)为下一插补点C, 直线段AC(AC=△L)为本次的合成进给量，D为AC的中点，6为本次插补的逼近 误差。由图的几何关系可得： P.(x y) 02 0 图2-26 时间分割法圆弧插补 △4BCx△ODym 那么有 =+h 则有 () 由于△y,、6都为未知数，故对上式进行如下近似处理： 由于△L很小，可用Ay代替4y,: 由于R)8,可用R代R.6。 由此有 cosY,≈(y-Ay/2)/R 式中的△y是由上一次插补运算中自动生成的。但是在开始时是没有Ay。的，可采 用如下算法求取该值： △xo=L/R Ay%=△Lx。/R 式中(x。、)为插补圆弧的起点。 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 2 二、讲稿 第二章 计算机数控系统 第二节 计算机数控系统的基本原理 3．圆弧插补算法 采用时间分割法进行圆弧插补的基本方法是用内接弦线逼近圆弧。只要在插补过程 中根据半径合理选用进给速度 F，就可以使逼近精度满足要求。 同直线插补一样，在设计圆弧插补程序时，为了简化程序设计，通常将插补计算坐 标系的原点选在被插补圆弧的圆心上，如图所示，以第一象限顺圆插补（G02）为例讨 论圆弧插补原理。图中 ( , ) i i i P x y 为圆上某一插补点 A， ( , ) i+1 i+1 i+1 P x y 为下一插补点 C， 直线段 AC（ AC = L ）为本次的合成进给量，D 为 AC 的中点，  为本次插补的逼近 误差。由图的几何关系可得： 图 2-26 时间分割法圆弧插补 ABC  ODy m 那么有 2 i i i     = + 则有 ( ) ) 2 ( ( ) ) 2 cos cos(      −  − = − =  = + R y Y R y i i m i i 由于 i y 、 都为未知数，故对上式进行如下近似处理： 由于 L 很小，可用  i−1 y 代替 i y ； 由于 R ，可用 R 代 R- 。 由此有 cos i  (yi − yi−1 2) R 式中的  i−1 y 是由上一次插补运算中自动生成的。但是在开始时是没有 0 y 的，可采 用如下算法求取该值： x0 = L y0 R y0 = Lx0 / R 式中（ 0 x 、 0 y ）为插补圆弧的起点。 则

数控技术及应用数案及讲癌 上部分：数控技术及编程 △x,=△Lcosy,=AL(y,-Ay-/2)/R △y,=y,-VR2-(x,+△x,)2 整理得 △x,=△Ly,-Ay-/2)/R H=+△ 式1 1=VR2-x3 △y=y-y 同直线插补一样，除上述算法外，还可以用下面的算法，即 Ay,=△L(x,+△x-/2)/R yi =y:-Ayi x=VR2-yn 式2 △x,=x1-X 由算式1、2中由第一个增量求得第二个增量的算法是 △y=y-VR2-(x,+△x,)月 式3 △x,=R2-y,-△y,)2-x 式4 分别对式3、4两边微分得 X.+△x: dAy,= dAx =x/ydax, 式5 VR2-(x,+△x,) dAx,= y-△y day,=ym/day, 式6 NR2-0y-△y) 由此可得，当xy时： 对式5有： d(△y,Kd(△x, 该算法对误差有收敛作用： 对式6有： ld(Ax,(Ay,) 该算法对误差有放大作用。 通过上面的分析，可得出如下结论： 当x,2y,时，采用先算△x的方法 当,时，采用先算△y的方法 该结论的实质是在插补计算时总是先算大的坐标增量，后算小的坐标增量。若再考 虑不同的象限，不同插补方向(G02G03),则插补公式将有16组。为了程序设计的方 便，可引入引导坐标的概念，即在采样周期内，将进给增量值较大的坐标定义为引导坐 标G,进给增量值较小的坐标定义为非引导坐标N。由于引入引导坐标的概念， 便将插 补计算公式归纳为2组 第一组：(A) △G,=△L(N,-△Na/2)/R G1=G+△G N=R-Gi AN,=N,-N,. 第二组：(B) 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 3 2 2 1 ( ) cos ( / 2)/ i i i i i i i i y y R x x x L L y y R  = − − +  =  =  −  −  整理得 1 2 1 2 1 1 1 ( / 2)/ + + + + −  = − = − = +   =  −  i i i i i i i i i i i y y y y R x x x x x L y y R 式 1 同直线插补一样，除上述算法外，还可以用下面的算法，即 i i i i i i i i i i i x x x x R y y y y y L x x R  = − = − = −   =  +  + + + + − 1 2 1 2 1 1 1 ( / 2)/ 式 2 由算式 1、2 中由第一个增量求得第二个增量的算法是 2 2 ( ) i i i i y = y − R − x + x 式 3 i i i i x = R − y − y − x 2 2 ( ) 式 4 分别对式 3、4 两边微分得 i i i i i i i i i d x x y d x R x x x x d y  =  − +  +   = +1 +1 2 2 ( ) 式 5 i i i i i i i i i d y y x d y R y y y y d x  =  − −  −   = +1 +1 2 2 ( ) 式 6 由此可得，当 +1 +1  i i x y 时： 对式 5 有： ( ) ( ) i i d y  d x 该算法对误差有收敛作用； 对式 6 有： ( ) ( ) i i d x  d y 该算法对误差有放大作用。 通过上面的分析，可得出如下结论： 当 i i x  y 时，采用先算 x 的方法； 当 i i x  y 时， 采用先算 y 的方法。 该结论的实质是在插补计算时总是先算大的坐标增量，后算小的坐标增量。若再考 虑不同的象限，不同插补方向（G02/G03），则插补公式将有 16 组。为了程序设计的方 便，可引入引导坐标的概念，即在采样周期内，将进给增量值较大的坐标定义为引导坐 标 G，进给增量值较小的坐标定义为非引导坐标 N。由于引入引导坐标的概念，便将插 补计算公式归纳为 2 组。 第一组：（A） 1 2 1 2 1 1 1 ( / 2)/ + + + + −  = − = − = +   =  −  i i i i i i i i i i i N N N N R G G G G G L N N R 第二组：（B）

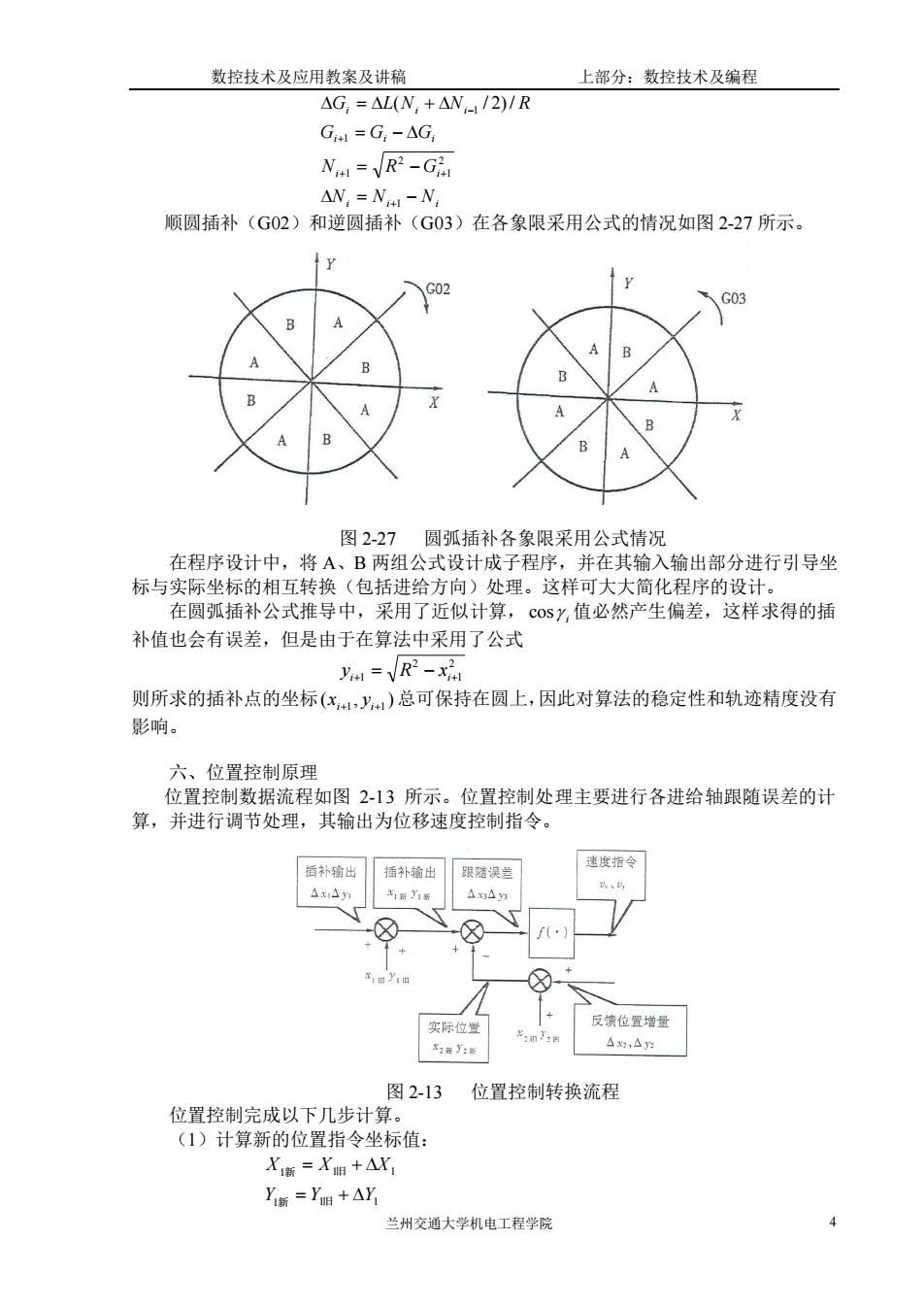
数控技术及应用教案及讲稿 上部分：数控技术及编程 △G,=△L(W,+△N-/2)/R G1=G,-△G, N=R2-G AN,=N-N, 顺圆插补(G02)和逆圆插补(G03)在各象限采用公式的情况如图2-27所示。 网))7圆[插补冬免限采用公式情识 在程序设计中，将A、B两组公式设计成子程序，并在其输入输出部分进行引导坐 标与实际坐标的相互转换（包括进给方向）处理。这样可大大简化程序的设计。 在圆弧插补公式推导中，采用了近似计算，csy,值必然产生偏差，这样求得的插 补值也会有误差，但是由于在算法中采用了公式 y=R2-x2 则所求的插补点的坐标(x,y)总可保持在圆上，因此对算法的稳定性和轨迹精度没有 影响。 六、位置控制原理 位置控制数据流程如图2-13所示。位置控制处理主要进行各进给轴跟随误差的计 算，并进行调节处理，其输出为位移速度控制指令。 补出 14 反资他置增品 #.n △2△： 图2-13位置控制转换流程 位置控制完成以下几步计 (1)计算新的位置指令坐标值： X商=X相+△X Ys=Y+AY 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 4 i i i i i i i i i i i N N N N R G G G G G L N N R  = − = − = −   =  +  + + + + − 1 2 1 2 1 1 1 ( / 2)/ 顺圆插补（G02）和逆圆插补（G03）在各象限采用公式的情况如图 2-27 所示。 图 2-27 圆弧插补各象限采用公式情况 在程序设计中，将 A、B 两组公式设计成子程序，并在其输入输出部分进行引导坐 标与实际坐标的相互转换（包括进给方向）处理。这样可大大简化程序的设计。 在圆弧插补公式推导中，采用了近似计算， i cos 值必然产生偏差，这样求得的插 补值也会有误差，但是由于在算法中采用了公式 2 1 2 i+1 = − i+ y R x 则所求的插补点的坐标 ( , ) i+1 i+1 x y 总可保持在圆上，因此对算法的稳定性和轨迹精度没有 影响。 六、位置控制原理 位置控制数据流程如图 2-13 所示。位置控制处理主要进行各进给轴跟随误差的计 算，并进行调节处理，其输出为位移速度控制指令。 图 2-13 位置控制转换流程 位置控制完成以下几步计算。 （1）计算新的位置指令坐标值： 1 1 1 1 1 1 Y Y Y X X X = +  = +  新 旧 新 旧

数控技术及应用数案及讲癌 上部分：数控技术及编程 (2)计算新的位置实际坐标值： X2新=X2相+△X2 =Y,+△Y △X3=X题-X2 △Y3=Y-Y (4)计算速度指令值 =f△X) V.=f(AY) 这里)是位置环的调节控制算法，具体的算法视具体系统而定。这一步在有些系 统中采用硬件来实现的 。Vx、送给伺服驱动单元，控制电机驱动俩执行部件以某 速度移动一个距离，以实现CNC装置的轨迹控制。 七、加减速控制 在CNC装置中，为了保证机床在启动或停止时不产生冲击、失步、超程或振荡， 必须对送到进给电机的进给脉冲频率或电压进行加减速控制。即在机床加速启动时，保 证加在伺服电机上的进给脉冲频率或电压逐渐增大而当机床减速停止时，保证加在同 服电机上的进给脉冲频率或电压逐渐减小 在CNC装置中，加减速控制多数都采用软件来实现，这样给系统带来了较大的灵 活性。这种用软件实现的加减速控制可以放在插补前进行，也可以放在插补后进行。放 在插补前的加减速控制称为前加减速控制，放在插补后的加减速控制称为后加减速控 制，如图2-28所示。 指令速度 Ar Ar 咸速 后加减速 插补 器 Ay 后加减速 几几 坐标位置x,y 图2-28前加减速和后加减速 前加诚速控制的优点是仅对合成速度一一编程指令速度F进行控制，所以它不会影响实 际插补输出的位置精度。前加减速控制的缺点是需要预测减速点，而这个减速点要根据 实际刀具位置与程序段终点之间的距离来确定，而这种预测工作需要完成的计算量较 大。 后加减速控制与前加减速控制相反，它是对各运动轴分别进行加减速控制，这种加 减速控制不需专门预测减速点，而是在插补输出为零时开始减速，并通过一定的时间延 迟逐渐靠近程序段终点。后加减速的缺点是，由于它对各运动坐标轴分别进行控制，所 以在加减速控制以后，实际的各坐标轴的合成位置就可能不准确。但是这种影响仅在加 速或减速过程中才会有，当系统进入匀速状态时，这种影响就不存在了。 (一入、前加减速控制 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 5 （2）计算新的位置实际坐标值： 2 2 2 2 2 2 Y Y Y X X X = +  = +  新 旧 新 旧 （3）计算跟随误差（指令位置指-实际位置值）： 新 新 新 新 3 1 2 3 1 2 Y Y Y X X X  = −  = − （4）计算速度指令值 ( ) ( ) 3 3 V f Y V f X y x =  =  这里 f(.)是位置环的调节控制算法，具体的算法视具体系统而定。这一步在有些系 统中采用硬件来实现的。Vx、Vy 送给伺服驱动单元，控制电机驱动俩执行部件以某一 速度移动一个距离，以实现 CNC 装置的轨迹控制。 七、加减速控制 在 CNC 装置中，为了保证机床在启动或停止时不产生冲击、失步、超程或振荡， 必须对送到进给电机的进给脉冲频率或电压进行加减速控制。即在机床加速启动时，保 证加在伺服电机上的进给脉冲频率或电压逐渐增大；而当机床减速停止时，保证加在伺 服电机上的进给脉冲频率或电压逐渐减小。 在 CNC 装置中，加减速控制多数都采用软件来实现，这样给系统带来了较大的灵 活性。这种用软件实现的加减速控制可以放在插补前进行，也可以放在插补后进行。放 在插补前的加减速控制称为前加减速控制，放在插补后的加减速控制称为后加减速控 制，如图 2-28 所示。 前加减速控制的优点是仅对合成速度——编程指令速度 F 进行控制，所以它不会影响实 际插补输出的位置精度。前加减速控制的缺点是需要预测减速点，而这个减速点要根据 实际刀具位置与程序段终点之间的距离来确定，而这种预测工作需要完成的计算量较 大。 后加减速控制与前加减速控制相反，它是对各运动轴分别进行加减速控制，这种加 减速控制不需专门预测减速点，而是在插补输出为零时开始减速，并通过一定的时间延 迟逐渐靠近程序段终点。后加减速的缺点是，由于它对各运动坐标轴分别进行控制，所 以在加减速控制以后，实际的各坐标轴的合成位置就可能不准确。但是这种影响仅在加 速或减速过程中才会有，当系统进入匀速状态时，这种影响就不存在了。 （一）、前加减速控制 图 2-28 前加减速和后加减速 ' x ' y y x ' F 坐标位置 x y, 指令速度 F 前 加 减 速 插 补 器 后加减速 后加减速 精 插 补