
Regression splines (parametric) Smoothing splines (nonparametric Basis functions for piecewise continuous models These constraints can be incorporated directly into the basis functions: h1(z)=1,h2(r)=x,hg(x)=(x-51)+,h4(r)=(x-2)+, where()+denotes the positive portion of its argument: Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) Basis functions for piecewise continuous models These constraints can be incorporated directly into the basis functions: h1(x) = 1, h2(x) = x, h3(x) = (x − ξ1)+, h4(x) = (x − ξ2)+, where (·)+ denotes the positive portion of its argument: r+ = ( r if r ≥ 0 0 if r < 0 Patrick Breheny STA 621: Nonparametric Statistics

Regression splines(parametric) Smoothing splines (nonparametric) Basis functions for piecewise continuous models o It can be easily checked that these basis functions lead to a composite function f(z)that: Is everywhere continuous Is linear everywhere except the knots Has a different slope for each region Also,note that the degrees of freedom add up:3 regions x 2 degrees of freedom in each region-2 constraints =4 basis functions Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) Basis functions for piecewise continuous models It can be easily checked that these basis functions lead to a composite function f(x) that: Is everywhere continuous Is linear everywhere except the knots Has a different slope for each region Also, note that the degrees of freedom add up: 3 regions × 2 degrees of freedom in each region - 2 constraints = 4 basis functions Patrick Breheny STA 621: Nonparametric Statistics

Regression splines (parametric Smoothing splines (nonparametric Splines o The preceding is an example of a spline:a piecewise m-1 degree polynomial that is continuous up to its first m-2 derivatives o By requiring continuous derivatives,we ensure that the resulting function is as smooth as possible o We can obtain more flexible curves by increasing the degree of the spline and/or by adding knots o However,there is a tradeoff: Few knots/low degree:Resulting class of functions may be too restrictive(bias) Many knots/high degree:We run the risk of overfitting (variance) Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) Splines The preceding is an example of a spline: a piecewise m − 1 degree polynomial that is continuous up to its first m − 2 derivatives By requiring continuous derivatives, we ensure that the resulting function is as smooth as possible We can obtain more flexible curves by increasing the degree of the spline and/or by adding knots However, there is a tradeoff: Few knots/low degree: Resulting class of functions may be too restrictive (bias) Many knots/high degree: We run the risk of overfitting (variance) Patrick Breheny STA 621: Nonparametric Statistics

Regression splines (parametric) Smoothing splines (nonparametric The truncated power basis o The set of basis functions introduced earlier is an example of what is called the truncated power basis o Its logic is easily extended to splines of order m: hj(c)=x3-1j=1..,m hm+k(c)=(z-5k)P-11=1,,K o Note that a spline has m+K degrees of freedom Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) The truncated power basis The set of basis functions introduced earlier is an example of what is called the truncated power basis Its logic is easily extended to splines of order m: hj (x) = x j−1 j = 1, . . . , m hm+k(x) = (x − ξk) m−1 + l = 1, . . . , K Note that a spline has m + K degrees of freedom Patrick Breheny STA 621: Nonparametric Statistics
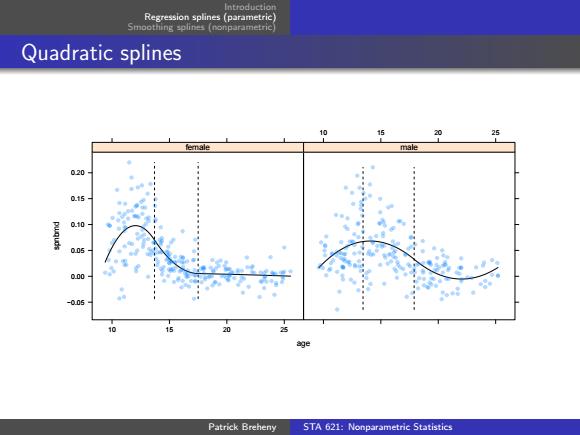
Regression splines (parametric) Smoothing splines (nonparametric Quadratic splines 20 25 male 020 015 0.05 0.00 -0.05 20 的日 Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) Quadratic splines age spnbmd −0.05 0.00 0.05 0.10 0.15 0.20 10 15 20 25 female 10 15 20 25 male Patrick Breheny STA 621: Nonparametric Statistics