
Regression splines (parametric Smoothing splines (nonparametric Global versus local bases o However,polynomial bases with global representations have undesirable side effects:each observation affects the entire curve,even for c values far from the observation o In previous lectures,we got around this problem with local weighting o In this lecture,we will explore instead an approach based on piecewise basis functions o As we will see,splines are piecewise polynomials joined together to make a singe smooth curve Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) Global versus local bases However, polynomial bases with global representations have undesirable side effects: each observation affects the entire curve, even for x values far from the observation In previous lectures, we got around this problem with local weighting In this lecture, we will explore instead an approach based on piecewise basis functions As we will see, splines are piecewise polynomials joined together to make a singe smooth curve Patrick Breheny STA 621: Nonparametric Statistics

Regression splines(parametric) Smoothing splines (nonparametric The piecewise constant model o To understand splines,we will gradually build up a piecewise model,starting at the simplest one:the piecewise constant model o First,we partition the range of z into K+1 intervals by choosing K points called knots o For our example involving bone mineral density,we will choose the tertiles of the observed ages Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) The piecewise constant model To understand splines, we will gradually build up a piecewise model, starting at the simplest one: the piecewise constant model First, we partition the range of x into K + 1 intervals by choosing K points {ξk} K k=1 called knots For our example involving bone mineral density, we will choose the tertiles of the observed ages Patrick Breheny STA 621: Nonparametric Statistics

Regression splines (parametric Smoothing splines (nonparametric The piecewise constant model (cont'd) 25 male 020 0.00 -005 20 的 Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) The piecewise constant model (cont’d) age spnbmd −0.05 0.00 0.05 0.10 0.15 0.20 10 15 20 25 female 10 15 20 25 male Patrick Breheny STA 621: Nonparametric Statistics
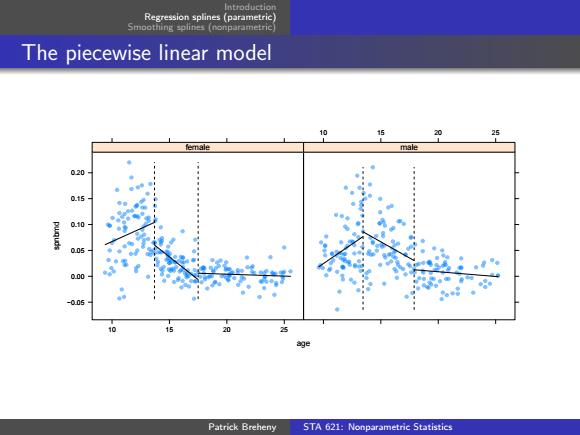
Regression splines (parametric) Smoothing splines (nonparametric The piecewise linear model 20 25 male 020 015 0.00 -005 20 Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) The piecewise linear model age spnbmd −0.05 0.00 0.05 0.10 0.15 0.20 10 15 20 25 female 10 15 20 25 male Patrick Breheny STA 621: Nonparametric Statistics
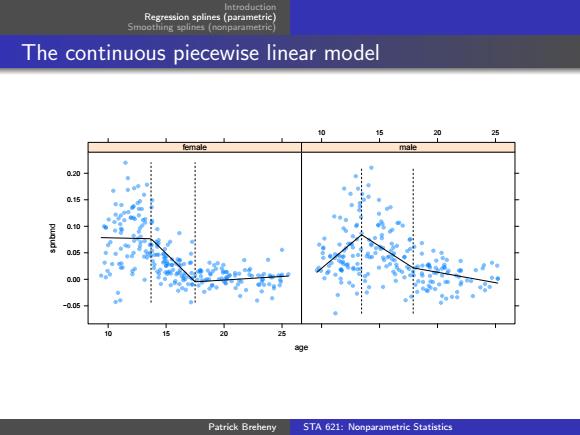
Regression splines (parametric Smoothing splines (nonparametric The continuous piecewise linear model 25 male 0.20 0.15 0 .05 C.00 -0.05 20 25 age Patrick Breheny STA 621:Nonparametric Statistics
Introduction Regression splines (parametric) Smoothing splines (nonparametric) The continuous piecewise linear model age spnbmd −0.05 0.00 0.05 0.10 0.15 0.20 10 15 20 25 female 10 15 20 25 male Patrick Breheny STA 621: Nonparametric Statistics