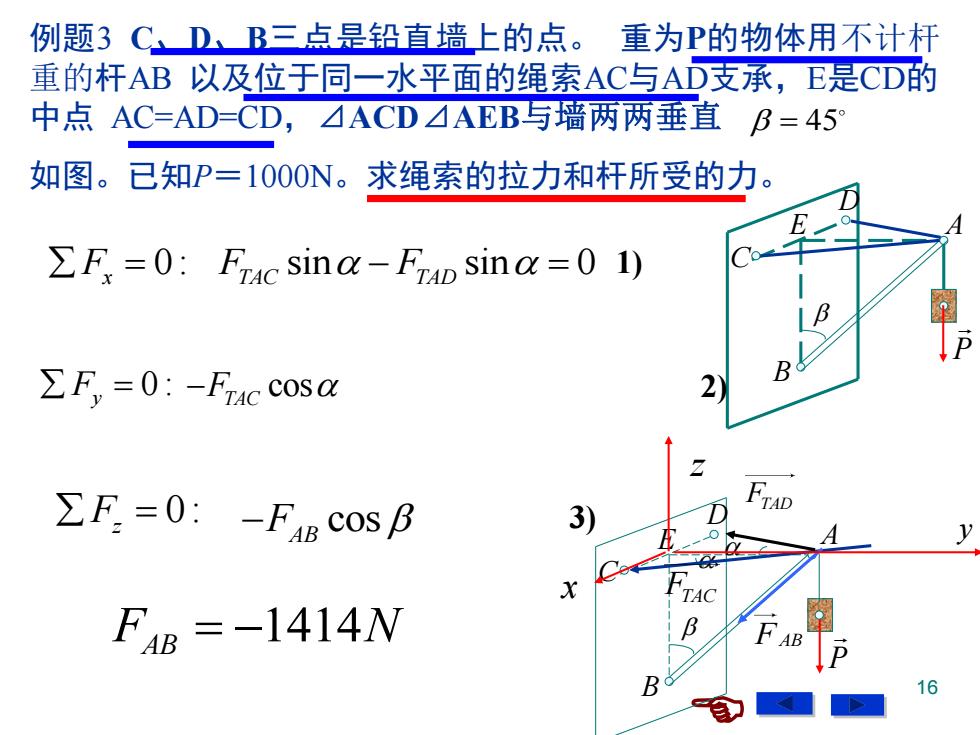
例题3C、DB三点是铅直墙上的点。重为P的物体用不计杆 重的杆AB以及位于同一水平面的绳索AC与AD支承,E是CD的 中点AC=AD=CD,△ACD AEB与墙两两垂直B=45° 如图。已知P=1000N。求绳索的拉力和杆所受的力。 F=0:Frac sina-FTaD sin=0 1) 5 ∑F=0:-F4ccos ∑F=0:-FB COS B TAD y FB=-1414W B 16
16 A B C D E P 例题3 C、D、B三点是铅直墙上的点。 重为P的物体用不计杆 重的杆AB 以及位于同一水平面的绳索AC与AD支承,E是CD的 中点 AC=AD=CD,⊿ACD⊿AEB与墙两两垂直 如图。已知P=1000N。求绳索的拉力和杆所受的力。 0 : = F x 0 : = F y 0 : = F z 1414 F N AB = − cos 0 − − = F P AB = 45 B C D E A P FTAD FTAC FAB x y z sin sin 0 F F TAC TAD − = cos cos sin 0 − − − = F F F TAC TAD AB 1) 2) 3)
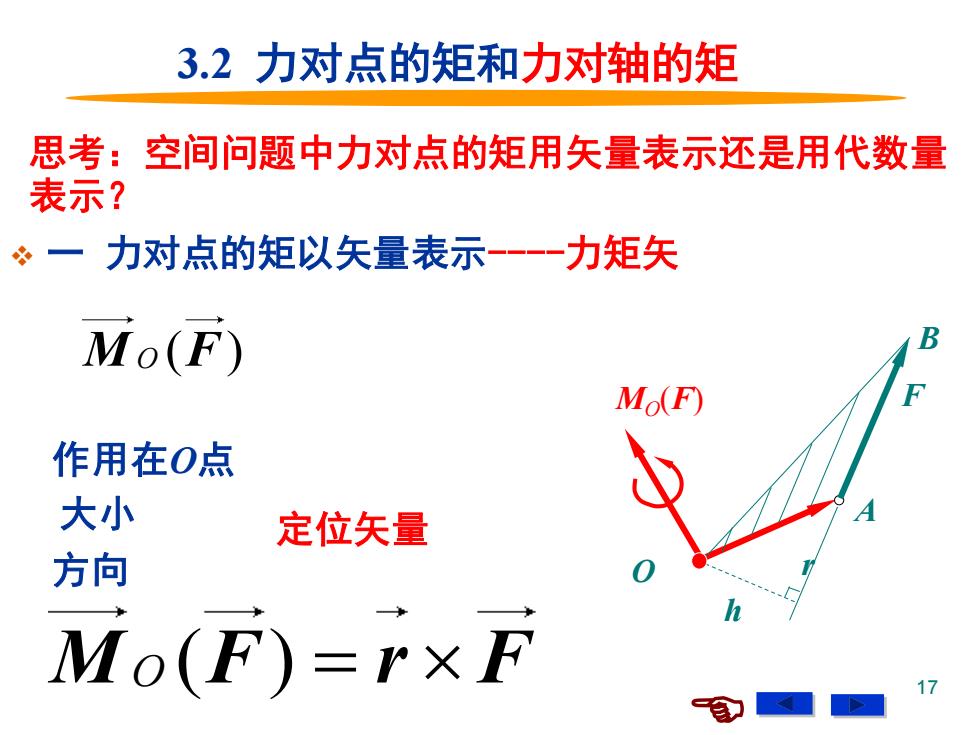
3.2力对点的矩和力对轴的矩 思考:空间问题中力对点的矩用矢量表示还是用代数量 表示? ÷一力对点的矩以矢量表示-一一一力矩矢 Mo(F) B M(F) 作用在0点 大小 定位矢量 方向 Mo(F)=rx F
17 3.2 力对点的矩和力对轴的矩 ❖ 一 力对点的矩以矢量表示-力矩矢 M F O ( ) O r MO(F) 思考:空间问题中力对点的矩用矢量表示还是用代数量 表示? M F r F O ( ) = 作用在O点 定位矢量 F B 大小 A 方向 h
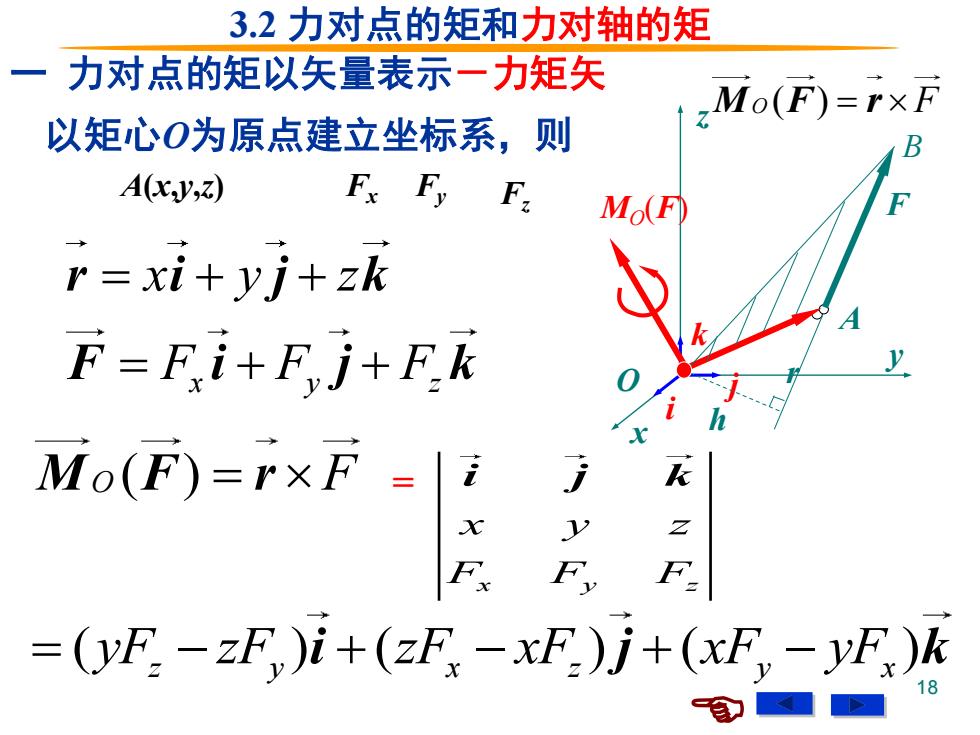
3.2力对点的矩和力对轴的矩 一 力对点的矩以矢量表示一力矩 Mo(F)=rxF 以矩心O为原点建立坐标系,则 A(xv,z) Fx Fy F Mo(F) r =xi+yj+zk F=Fi+Fj+Fk Mo(F)=r×F=|i k =(yF:-zF,)i+(zF,-xF)j+(xF,-yF)k 8
18 以矩心O为原点建立坐标系,则 x y z x y z F F F = + + = + + r i j k F i j k M F r O ( ) = F A(x,y,z) x y z j i k 一 力对点的矩以矢量表示-力矩矢 x y z x y z F F F i j k ( ) ( ) ( ) z y x z y x = − + − + − yF zF zF xF xF yF i j k = F B A O r MO(F) h Fx Fy Fz M F r O ( ) = F 3.2 力对点的矩和力对轴的矩
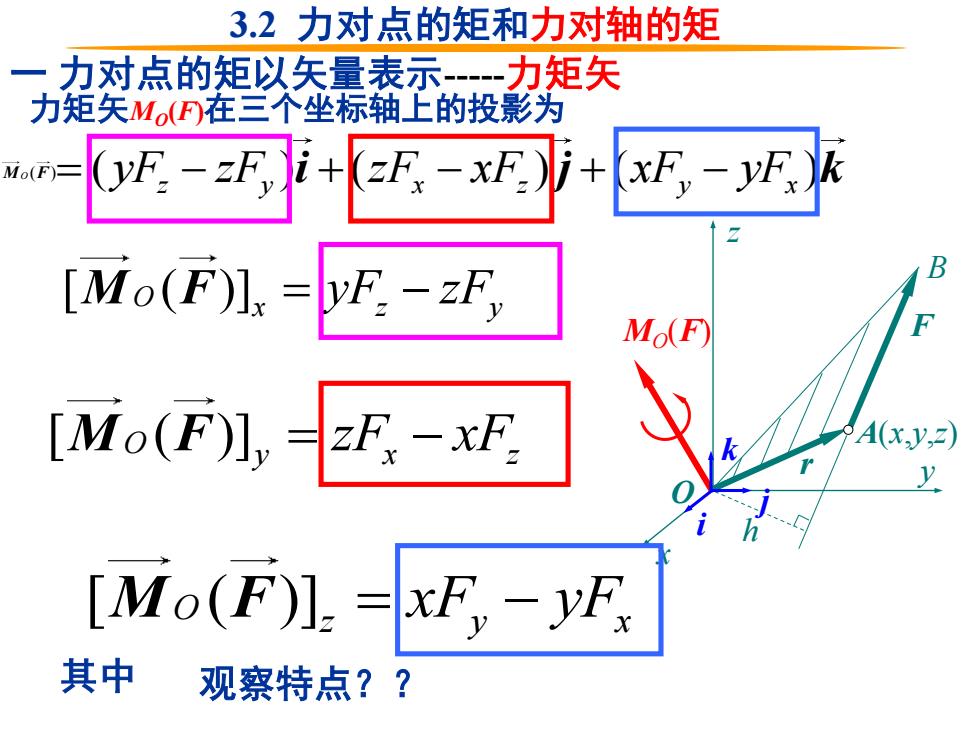
32力对点的矩和力对轴的矩 一力对点的矩以矢量表示-一力矩矢 力矩矢MoF在三个坐标轴上的投影为 Mo(F)- 0s-+项:- i+F-明 [Mo(F】=yF:-zF Mo(F) [Mo(F】2zR-xF A(x.y,=) [Mo(F】=xF,-F 其中 观察特点??
力矩矢MO(F)在三个坐标轴上的投影为 [ ( )] O x z y M F = − yF zF x y z O M F O(F) r A(x,y,z) h B j i k 一 力对点的矩以矢量表示-力矩矢 [ ( )] O y x z M F = − zF xF [ ( )] O z y x M F = − xF yF ( ) ( ) ( ) z y x z y x = − + − + − yF zF zF xF xF yF i j k 其中 观察特点?? 3.2 力对点的矩和力对轴的矩 M F O ( )

3.2力对点的矩和力对轴的矩 二★★力对轴的矩 思考:力对轴的矩用代数量表示? 1力F对z轴的矩定义为: M(F)= 按右手螺旋法则确定其正负号 思考:什么情况下力对轴的矩等于零? 力与坐标轴相交力与坐标轴平行 力与轴共面时 21
21 1 力F对z 轴的矩定义为: ( ) ( ) 2 M M F h A z O xy xy Oab F F = = = 二 ★ ★力对轴的矩 z F B A 按右手螺旋法则确定其正负号 思考:力对轴的矩用代数量表示? 思考:什么情况下力对轴的矩等于零? 力与轴共面时 y x O a Fxy h b 3.2 力对点的矩和力对轴的矩 力与坐标轴相交 力与坐标轴平行