
X .无机材料物理性能 7.3.3电击穿、.254 7.3.4无机材料的击穿.256 7.4铁电性. 258 7.41铁电体 . 258 7.4.2钛酸钡自发极化的微观机理.259 7.4.3 铁电. 261 7.4.4铁电体的性能及其应用.263 7.5压电性. 266 7.5.1压电效应 . 266 7.5.2压电振子及其参数 270 7.5.3压电性与晶体结构. 272 习题 276 第8章 无机材料的磁学性能.277 8.1物质的磁性. 277 8.1.1 磁现象及其物理量 277 8.1.2 磁性的本质 279 8.1.3磁性的分类. 282 8.2磁畴与磁滞回线. 286 821磁。 286 8.2.2 破活回线.4.。.,。 286 8.2.3磁导率 287 8.3铁氧体的磁性与结构.288 8.3.1 尖晶石型铁氧体 .288 8.3.2石榴石型铁氧体 290 8,3.3磁船石刊铁氧体 8.4铁氧体磁性材料. .291 8.4.1 软磁材料.291 8.4.2 硬磁材料 .292 8.4.3 旋磁材料 292 8,445磁材料:,。,。,。 293 8.4.5压磁材料 ,294 习题.294 参考文献 .295
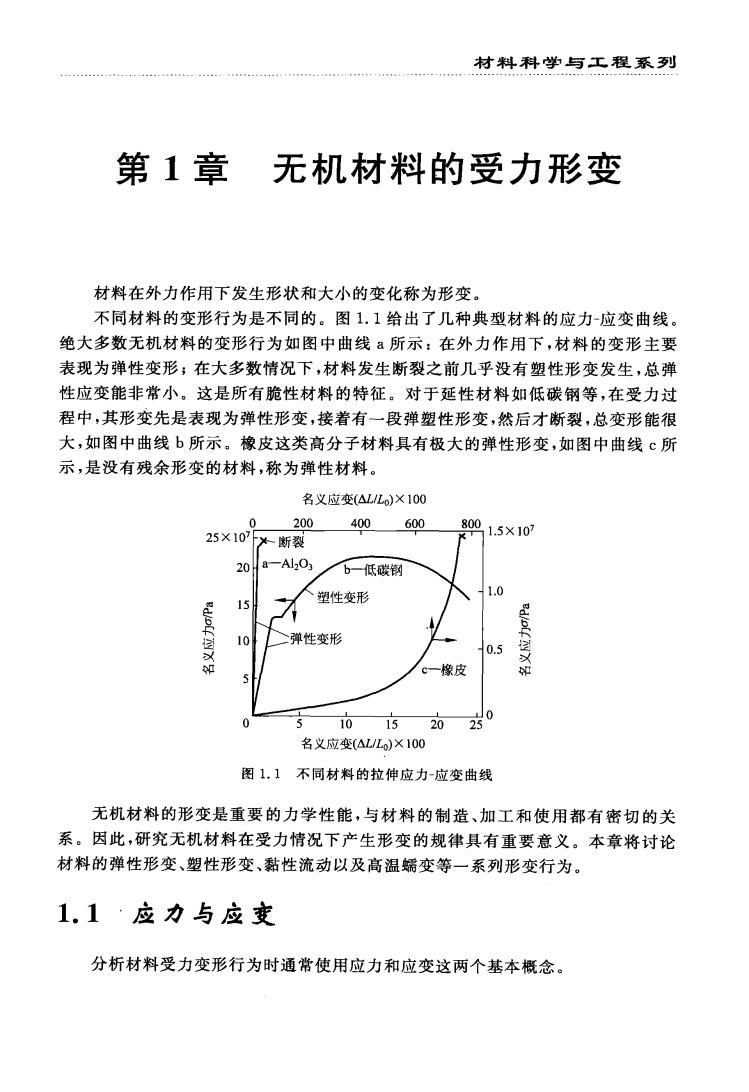
材料科学与工程系列 第1章 无机材料的受力形变 材料在外力作用下发生形状和大小的变化称为形变 不同材料的变形行为是不同的。图1.1给出了几种典型材料的应力-应变曲线」 绝大多数无机材料的变形行为如图中曲线a所示:在外力作用下,材料的变形主要 表现为弹性变形,在大多数情况下,材料发生断裂之前几乎没有塑性形变发生,总弹 性应变能非常小。这是所有脆性材料的特征。对于延性材料如低碳钢等,在受力过 程中,其形变先是表现为弹性形变,接着有一段弹塑性形变,然后才断裂,总变形能很 大,如图中曲线b所示。橡皮这类高分子材料具有极大的弹性形变,如图中曲线c所 示,是没有残余形变的材料,称为弹性材料。 名义应变(△L/Lo)×10( 25x10 .200 400600 断裂 8001.5×10 20Ha-AlzO 一低碳钢 人塑性变形 1.0 15 10 弹性变形 一橡皮 15 20 20 名义应变(△L/Lo)×100 图11不同材料的拉伸应力-应变曲线 无机材料的形变是重要的力学性能,与材料的制造、加工和使用都有密切的关 系。因此,研究无机材料在受力情况下产生形变的规律具有重要意义。本章将讨论 材料的弹性形变、塑性形变、黏性流动以及高温蠕变等一系列形变行为。 1.1‘应力与应变 分析材料受力变形行为时通常使用应力和应变这两个基本概念

.无机材料物理性能. 1.1.1应力 应力一般定义为材料单位面积所受的内力,即: 。= (1.1) 式中,F为外力;A为面积,σ为应力。应力的单位为Pa,但在实际应用中经常采用 MPa作为应力单位:1MPa=10sPa。 如果式(1.1)中面积A取材料受力前的初始面积A。,则=F/A。称为名义应 力。如果式(1.1)中的A为受力后的真实面积,则。称为真实应力。无机材料的形 变总量通常很小,因此真实应力与名义应力在数值上一般相差不大,只有在材料发生 了高温蠕变的情况下才有显著差别。在实际应用中一般都采用名义应力。 围绕材料内部任意一点P取一体积单元,体积元的6个面均垂直于坐标轴x、y、 z。在这6个面上的作用应力可分解为法向应力 gngn、n和剪应力ty、ta,c.等,每个面上有一 个法向应力。和两个剪应力x,如图1.2所示 应力分量、x的下标第一个字母表示应力作用面 的法线方向,第二个字母则表示应力作用的方 向。法向应力的正值表示拉应力,负值则表示压 应力。剪应力分量的正负规定如下:如果体积元 任一面上的法向应力与坐标轴的正方向相同,则 该面上的剪应力指向坐标轴的正方向者为正:如 图1.2应力分量 果该面上的法向应力指向坐标轴的负方向,则剪 应力指向坐标轴的负方向者为正。根据上述规定,图1.2上所表示的所有应力分量 都是正的。 根据平衡条件,体积元上两相对平行平面上的法向应力应该是大小相等、正负号 相同,而作用在体积元上任一平面上的两个剪应力则应互相垂直。此外,根据剪应力 互等定理,=x,余类推。因此,材料内部任意一点处的应力状态可以由6个应力 分量决定,即:=n0::。对于法向应力分量。其下标可以略去一个字 母,写成4、0a4。 法向应力导致材料的伸长或缩短,剪应力引起材料的剪切畸变。 1.1.2应变 应变描述的是在外力作用下物体内部各质点之间的相对位移,应变可分为正应 变和剪切应变两类。 考虑一根长度为L。的杆在单向拉应力作用下被拉长到L,相应的正应变可以 定义为

3 :第1章无机材料的受力形变 -兴 (1.2) Lo 式中的ε称为名义应变。如果式(1.2)中的分母不是杆的初始长度L,而是随拉伸 而变化的真实长度L,则可以定义真实应变em为 (1.3) 通常为了方便起见都用名义应变。 由式(1.2)和式(1.3)可知,应变是一个 无量纲的物理量。 B 材料在剪应力作用下会发生剪切应变。 剪切应变定义为物体内部一体积元上的两 个面元(或特征面上的两个线元)之间夹角 的变化。以如图1.3所示垂直于x轴截面 上的形变情况为例,在剪应力作用下,线元 OA及OB之间的夹角由受力前的∠AOB 变化为受力后的∠A'OB',则x、y之间的剪 切应变Y,可以定义为 图1,3之面上的剪应力和剪切应变 Y一&十B (1.4) 和研究应力状态一样,研究物体中任意一点(如O点)的应变状态,也需要在物 体内围绕该点取出一体积元drdydz。假设在外力作用下物体发生形变,导致O点 沿xy、之方向的产生分量分别为u、w的位移。考虑x轴上O点邻近处的一点A 如图1.3所示,由于O点有位移,A点位移随x的增加而增加,该点处的位移将是 u+dx,即线元OA的长度增加了z,因此,在O点处沿x方向的正应变(单位 伸长)为。一器/血-器同理可得,c。器。一肥 现在考查线段OA及OB之间的夹角变化。如图1.3所示,A点沿y方向的位 移为十,B点沿工方向的位移为u十。由于这些位移,线段OA的新方向 0A'与原来的方向之间的畸变夹角为(+驶-)×击-职、同理,OB与0B 之间的畸变夹角为器。由此可见,线段OA与OB之间原来的直角∠AOB在变形之 后变化了+器因此,围绕O点的体积单元上各剪切应变分量分别为

.无机材料物理性能 %一器+器 -是+器 (1.5) a-+歌 和一点的应力状态可由6个应力分量来决定一样,一点的应变状态也可以由与 应力分量对应的6个应变分量来决定:即3个剪切应变分量YyY及3个正应变 分量eaE物ea。同法向应力一样,正应变分量的下标也可以省去一个字母,写成e,。 有了应力、应变分量就可定量地研究物体的受力形变。 1.2无机材料的弹性形变 1.2.1各向同性体的弹性常数 在所受应力不太高的情况下,无机材料、金属、木材等许多重要材料在室温下通 常表现为单纯的弹性变形。材料在弹性形变阶段的应力-应变关系可以用胡克定律 加以描述。 如图1.4所示,考虑一各棱边分别平行于坐标轴的长方体,在垂直于x轴的两个 面上受均匀分布的正应力:作用。实验证明,对于各向同性体,这样的正应力不会 引起长方体的角度改变,而长方体在x轴方向上的相对伸长可以表示为: 6== (1.6) 即:在弹性形变阶段应力与应变之间为线性关系。这就是胡克定律。 垫 1 b 图1.4各向同性长方体受力形变示意图 式(1.6)中的物理量E称为材料的弹性模量(有时也称为杨氏模量)。对于各向 同性体,E是一个常数。由于应变e是一个无量纲物理量,由式(1.6)可知,弹性模量 的单位和应力一样,也是Pa。在实际应用中多采用GPa作为材料弹性模量的单位: 1GPa=10°Pa。 注意到当长方体伸长时,侧向同时也会发生横向收缩,如图1.4所示。6,单独 作用时,在y、z方向的收缩为