
金属氧化物中的缺陷平衡 本章基本要求 1.(重难点)熟练掌握各种金属氧化缺陷平衡关系式的推导,能够准确判断不同情 况下各种缺陷的数量关系和主次关系,并准确做出缺陷反应的Brouwer图. 2.能够准确推导TO2和BaTiO3等物质的缺陷平衡关系式,掌握电导率在缺陷平 衡中的应用. 3.1缺陷化学中的平衡热力学 在晶体中,理论上在0K以上都存在着缺陷,且各种缺陷都可以产生,但在特定的 晶体中某种缺陷可能成为主要缺陷.我们把缺陷看成溶质,把晶体本身看作溶剂。 1.点缺陷统计热力学模型 一个由N个原子构成的完美晶体由于热激发形成v个空位,有 △G=nv(△H-T△Sb)-T△Semf. (3.1.1) 其中,△H为缺陷形成焓,Sb为缺陷致振动嫡增,Sm为缺陷致构型熵增.根据 Boltzmann分布,有 △S=khw=knN+nv (3.1.2) Wlnw! 当x1时,有近似关系hx!=xn+x,因此 A-(+mh") (3.1.3) △G=maH-TASa)-kr(NmY++whN+) (3.1.4) N nv 49
3 金属氧化物中的缺陷平衡 本章基本要求 1.(重难点)熟练掌握各种金属氧化缺陷平衡关系式的推导,能够准确判断不同情 况下各种缺陷的数量关系和主次关系,并准确做出缺陷反应的 Brouwer 图. 2. 能够准确推导 TiO2 和 BaTiO3 等物质的缺陷平衡关系式,掌握电导率在缺陷平 衡中的应用. 3.1 缺陷化学中的平衡热力学 在晶体中,理论上在 0K 以上都存在着缺陷,且各种缺陷都可以产生,但在特定的 晶体中某种缺陷可能成为主要缺陷.我们把缺陷看成溶质,把晶体本身看作溶剂. 1. 点缺陷统计热力学模型 一个由 N 个原子构成的完美晶体由于热激发形成 nV 个空位,有 ∆G = nV (∆H − T ∆Svib) − T ∆Sconf . (3.1.1) 其中,∆H 为缺陷形成焓,Svib 为缺陷致振动熵增,Sconf 为缺陷致构型熵增.根据 Boltzmann 分布,有 ∆Sconf = kHMW = kHM(N + nV )! N!nV ! . (3.1.2) 当 x " 1 时,有近似关系 HMx! = xHMx + x,因此 ∆Sconf = k ! NHMN + nV N + nV HMN + nV nV " , (3.1.3) ∆G = nV (∆H − T ∆Svib) − kT ! NHMN + nV N + nV HMN + nV nV " . (3.1.4) 49
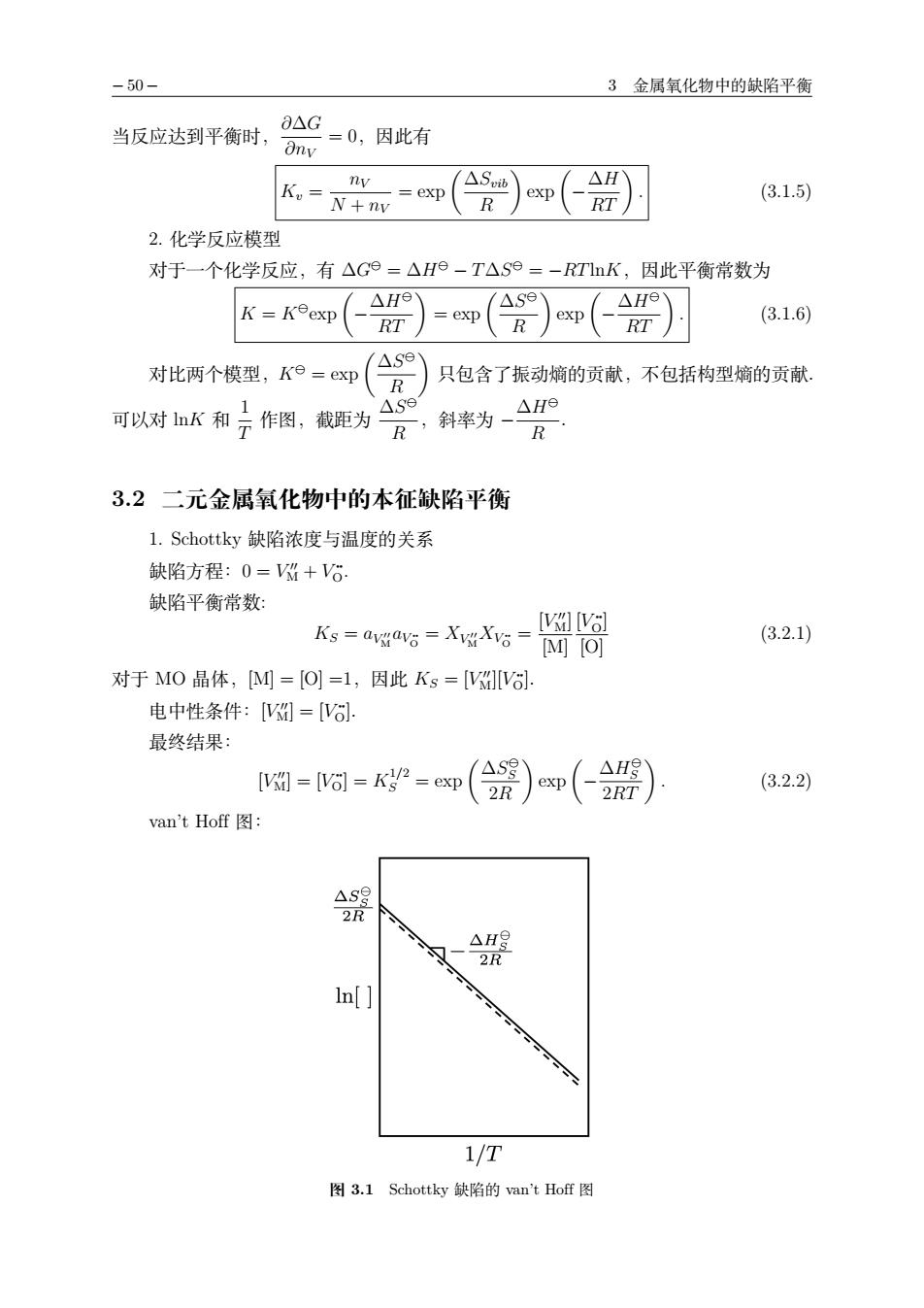
-50- 3金属氧化物中的缺陷平衡 当反应达到平衡时, 8△C=0,因此有 Ony (3.1.5) 2.化学反应模型 对于一个化学反应,有△G9=△H9-T△S9=-T血K,因此平衡常数为 (3.1.6) 对比两个模型,Ke=exp( )只包含了振动熵的贡献,不包括构型熵的贡献, 可以对K和子作图,截距为 R,斜率为-△H R 3.2二元金属氧化物中的本征缺陷平衡 1.Schottky缺陷浓度与温度的关系 缺陷方程:0=+6 缺陷平衡常数: kg=4gg=Xgg=阁阁 (3.2.1) 对于MO晶体,M=O1=1,因此Ks=VI6 电中性条件:[=[V6 最终结果: 网-a-k=m(紧)m(合器) (3.2.2) van't Hoff图: In[] 1/T 图3.1 Schottky缺陷的an'tHof图
− 50 − 3 金属氧化物中的缺陷平衡 当反应达到平衡时,∂∆G ∂nV = 0,因此有 Kv = nV N + nV = 2tT !∆Svib R " 2tT ! −∆H RT " . (3.1.5) 2. 化学反应模型 对于一个化学反应,有 ∆G! = ∆H! − T ∆S! = −RTHMK,因此平衡常数为 K = K!2tT ! −∆H! RT " = 2tT !∆S! R " 2tT ! −∆H! RT " . (3.1.6) 对比两个模型,K! = 2tT !∆S! R " 只包含了振动熵的贡献,不包括构型熵的贡献. 可以对 lnK 和 1 T 作图,截距为 ∆S! R ,斜率为 −∆H! R . 3.2 二元金属氧化物中的本征缺陷平衡 1. Schottky 缺陷浓度与温度的关系 缺陷方程:0 = V "" J + V •• P. 缺陷平衡常数: KS = aV !! JaV •• P = XV !! JXV •• P = [V "" J] [J] [V •• P] [P] (3.2.1) 对于 MO 晶体,[M]=[O] =1,因此 KS = [V "" J][V •• P]. 电中性条件:[V "" J]=[V •• P]. 最终结果: [V "" J]=[V •• P] = K1/2 S = 2tT !∆S! S 2R " 2tT ! −∆H! S 2RT " . (3.2.2) van’t Hoff 图: 图 3.1 Schottky 缺陷的 van’t Hoff 图

3.3非化学计量金属氧化物的缺陷平衡 -51- 2.Frenkel缺陷浓度与温度的关系 缺陷方程:M=M+V 缺陷平衡常数: (3.2.3) 对于MO晶体,M]=[]=1,因此KF=MV. 电中性条件:M]=, 最终结果: =阳=k-m(2)四(会) (3.2.4) 3.电子本征缺陷 缺陷方程:0=e+ 缺陷平衡常数: K=忘品 (3.2.5) R=即=NeWvep(F) (3.2.6) 电中性条件:n=p. 最终结果: n=p=k=cwam(2语) 3.2.7) 总结:对于本征缺陷,缺陷浓度 xm(会)m() (3.2.8) 主要由△H决定,且温度越高,缺陷浓度越高 3.3非化学计量金属氧化物的缺陷平衡 1.缺氧化合物MO1-x的缺陷平衡 缺陷方程:06=6+2E+0z(gas) 平衡常数: 隔()'(爱 (3.3.1) KVo Ne Kvo [Voln2po (3.3.2) 其中,[O】=1,p82=1bar. 电中性条件:n=2V 缺陷浓度与氧分压的关系 n=2Vo]=(2KV)1/3po:/6 Pol/e (3.3.3)
3.3 非化学计量金属氧化物的缺陷平衡 − 51 − 2. Frenkel 缺陷浓度与温度的关系 缺陷方程:J× J = J•• i + V "" J. 缺陷平衡常数: KF = [J•• i ] [J× J] [V "" J] [V × i ] , (3.2.3) 对于 MO 晶体,[J× J]=[V × i ] =1,因此 KF = [J•• i ][V "" J]. 电中性条件:[J•• i ]=[V "" J]. 最终结果: [J•• i ]=[V "" J] = K1/2 F = 2tT !∆S! F 2R " 2tT ! −∆H! F 2RT " . (3.2.4) 3. 电子本征缺陷 缺陷方程:0 = e" + h• . 缺陷平衡常数: Ki = n NC p NV , (3.2.5) K" i = np = NCNV 2tT !−Eg RT " . (3.2.6) 电中性条件:n = p. 最终结果: n = p = K"1/2 i = (NCNV ) 1/22tT !−Eg 2RT " . (3.2.7) 总结:对于本征缺陷,缺陷浓度 [ ] ∝ 2tT !∆S! F nk " 2tT ! −∆H! F nkT " (3.2.8) 主要由 ∆H! 决定,且温度越高,缺陷浓度越高. 3.3 非化学计量金属氧化物的缺陷平衡 1. 缺氧化合物 MO1−x 的缺陷平衡 缺陷方程:P× P = V •• P + 2e" + 1 2 P2(; b). 平衡常数: KVP = [V •• P] [P× P] ! n NC "2 !pP2 p! P2 "1/2 , (3.3.1) K" VP = N2 CKVP = [V •• P]n2 p 1/2 P2 , (3.3.2) 其中,[P× P]=1,p! P2 = 1bar. 电中性条件:n = 2[V •• P]. 缺陷浓度与氧分压的关系: n = 2[V •• P] = (2K" VP ) 1/3p −1/6 P2 ∝ p −1/6 P2 . (3.3.3)

52 3金属氧化物中的缺陷平衡 Brouwer图:log]-logpo,关系图 nninnn n=2时p ⊥⊥⊥⊥⊥L⊥IiIiIIII LOG Po2 图3.2缺氧化合物MO1-x的Brouwer图(Kofstad-Fig.3.2) 2.富金属化合物1M2+O3的缺陷平衡 缺陷方程:M+206=M+3+02(gas) 平衡常数: KSt [M7]n'po. (3.3.4) 电中性条件:n=3M] 缺陷浓度与氧分压的关系 n=3M1xpo8/16, (3.3.5) Brouwer图斜率:-3/16. 3.缺金属化合物M1-0的缺陷平衡 缺陷方程·02(ga9)=+2h+06 平衡常数 K=[VMlP2PoI2 (3.3.6 电中性条件:p=2阳 缺陷浓度与氧分压的关系: p=2[VM]Poe. 3.3.7 Brouwer图斜率:1/6. 4.富氧化合物MO1+z的缺陷平衡 缺陷方程:02(gas)=0+2. 平衡常数: Ko.=[oppo: (3.3.8) 电中性条件:p=2OW 缺陷浓度与氧分压的关系 p=210]Pos (3.3.9 Brouwer图斜率:1/6
− 52 − 3 金属氧化物中的缺陷平衡 Brouwer 图:log[ ]−logpP2 关系图. 图 3.2 缺氧化合物 MO1−x 的 Brouwer 图(Kofstad-Fig.3.2) 2. 富金属化合物 M2+xO3 的缺陷平衡 缺陷方程:J× J + 3 2 P× P = J••• i + 3e" + 3 4 P2(; b). 平衡常数: K" Ji = [J••• i ]n3 p 3/4 P2 . (3.3.4) 电中性条件:n = 3[J••• i ] 缺陷浓度与氧分压的关系: n = 3[J••• i ] ∝ p −3/16 P2 . (3.3.5) Brouwer 图斜率:−3/16. 3. 缺金属化合物 M1−xO 的缺陷平衡 缺陷方程:1 2 P2(; b) = V "" J + 2h• + P× P. 平衡常数: K" VJ = [V "" J]p2 p −1/2 P2 . (3.3.6) 电中性条件:p = 2[V "" J] 缺陷浓度与氧分压的关系: p = 2[V "" J] ∝ p 1/6 P2 . (3.3.7) Brouwer 图斜率:1/6. 4. 富氧化合物 MO1+x 的缺陷平衡 缺陷方程:1 2 P2(; b) = P"" i + 2h• . 平衡常数: K" Pi = [P"" i ]p2 p −1/2 P2 . (3.3.8) 电中性条件:p = 2[P"" i ] 缺陷浓度与氧分压的关系: p = 2[P"" i ] ∝ p 1/6 P2 . (3.3.9) Brouwer 图斜率:1/6.

3.4多缺陷共存的复杂缺陷平衡体系 -53- 3.4多缺陷共存的复杂缺陷平衡体系 1.基本目标:各种缺陷浓度与温度或氧分压的关系 2.基本步骤: (1)写出相关的独立的缺陷方程式和这些缺陷方程式的平衡常数,一般个缺陷 有n-1个方程: (2)写出包括所有缺陷在内的总的电荷平衡表达式: (3)确定一对主要缺陷,简化电荷平衡表达式: (4)根据简化后的电荷平衡表达式和相关的缺陷方程式计算主要缺陷的浓度与氧分 压的关系; (5)根据与其它缺陷相关的缺陷方程式,计算出非主要缺陷浓度与氧分压的关系: (6)根据各种缺陷浓度的变化趋势,确定随氧分压变化过程中出现的其他主要缺 陷,并利用上述步骤计算其他氧分压范围的缺陷浓度与氧分压的关系 (7)获得所有氧分压范围中所有缺陷与氧分压的关系. 3.5恒定掺杂浓度体系的缺陷平衡 在比较低的温度下,由于可能存在的掺杂原子的传输比较慢,掺杂或取代原子的浓 度被冻结,掺杂或取代物的浓度是恒定的,这存在着三种情况: (1)掺杂或取代量低于固溶的极限,这个系统是稳定的: (2)掺杂或取代量低于固溶的极限,但存在富掺杂或着取代物的第二相,这个系统 是亚稳的; (3)掺杂或取代量超过固溶的极限,这个系统是亚稳的, 3.6变化掺杂浓度体系的缺陷平衡 在比较高的温度下,掺杂原子的传输比较快,掺杂或取代原子处于化学平衡状态 存在两种情况: (1)掺杂量低于固溶极限,也没有富掺杂或取代物的第二相,掺杂或取代物的浓度 是恒定的 (2)摻杂量高于固溶极限,存在富掺杂或取代物的第二相,掺杂或取代物的浓度是 变化的. 3.7缺陷化学的应用 电导率σ与载流子浓度n,带电量Q和迁移率“成正比,即 a nQu (3.7.1) 其中,载流子可以为电子、空穴或其他离子,且它们的迁移率不同
3.4 多缺陷共存的复杂缺陷平衡体系 − 53 − 3.4 多缺陷共存的复杂缺陷平衡体系 1. 基本目标:各种缺陷浓度与温度或氧分压的关系. 2. 基本步骤: (1)写出相关的独立的缺陷方程式和这些缺陷方程式的平衡常数,一般 n 个缺陷 有 nɢ1 个方程; (2)写出包括所有缺陷在内的总的电荷平衡表达式; (3)确定一对主要缺陷,简化电荷平衡表达式; (4)根据简化后的电荷平衡表达式和相关的缺陷方程式计算主要缺陷的浓度与氧分 压的关系; (5)根据与其它缺陷相关的缺陷方程式,计算出非主要缺陷浓度与氧分压的关系; (6)根据各种缺陷浓度的变化趋势,确定随氧分压变化过程中出现的其他主要缺 陷,并利用上述步骤计算其他氧分压范围的缺陷浓度与氧分压的关系. (7)获得所有氧分压范围中所有缺陷与氧分压的关系. 3.5 恒定掺杂浓度体系的缺陷平衡 在比较低的温度下,由于可能存在的掺杂原子的传输比较慢,掺杂或取代原子的浓 度被冻结,掺杂或取代物的浓度是恒定的,这存在着三种情况: (1)掺杂或取代量低于固溶的极限,这个系统是稳定的; (2)掺杂或取代量低于固溶的极限,但存在富掺杂或着取代物的第二相,这个系统 是亚稳的; (3)掺杂或取代量超过固溶的极限,这个系统是亚稳的. 3.6 变化掺杂浓度体系的缺陷平衡 在比较高的温度下,掺杂原子的传输比较快,掺杂或取代原子处于化学平衡状态, 存在两种情况: (1)掺杂量低于固溶极限,也没有富掺杂或取代物的第二相,掺杂或取代物的浓度 是恒定的; (2)掺杂量高于固溶极限,存在富掺杂或取代物的第二相,掺杂或取代物的浓度是 变化的. 3.7 缺陷化学的应用 电导率 σ 与载流子浓度 n,带电量 Q 和迁移率 u 成正比,即 σ = nQu. (3.7.1) 其中,载流子可以为电子、空穴或其他离子,且它们的迁移率不同.