
标准误差与标准偏差的特点 1.标准误差相对真值而言,测定次数为 n→0o 2.标准偏差相对平均值而言,计算公式中 的n-1称为自由度(通俗的理解可为:做 了n次实验,有n-1次可以做对比) ●●●●●
标准误差与标准偏差的特点 1. 标准误差相对真值而言,测定次 数为 n→∞ 2. 标准偏差相对平均值而言,计算公式中 的n-1称为自由度(通俗的理解可为:做 了n次实验,有n-1次可以做对比)

精密度表示法小结 测定结果数据精密度的表示法有: 偏差(d) 平均偏差(d) 相对平均偏差 即精密度)》 标准偏差(s) X 相对标准偏差 (s 即:变异系数) x 工业生产中还常用极差和公差来表示,具体采用哪 一种表示法、由分析结果的要求决定。 另外:表示误差的数值时,用1-2位有效数字 00 即可
精密度表示法小结 • 测定结果数据精密度的表示法有: – 偏差(d) – 平均偏差( ) – 相对平均偏差( 即精密度) – 标准偏差(s) – 相对标准偏差( 即 :变异系数) d _ _x d _x S 工业生产中还常用极差和公差来表示,具体采用哪 一种表示法、由分析结果的要求决定。 另外:表示误差的数值时,用1-2位有效数字 即可
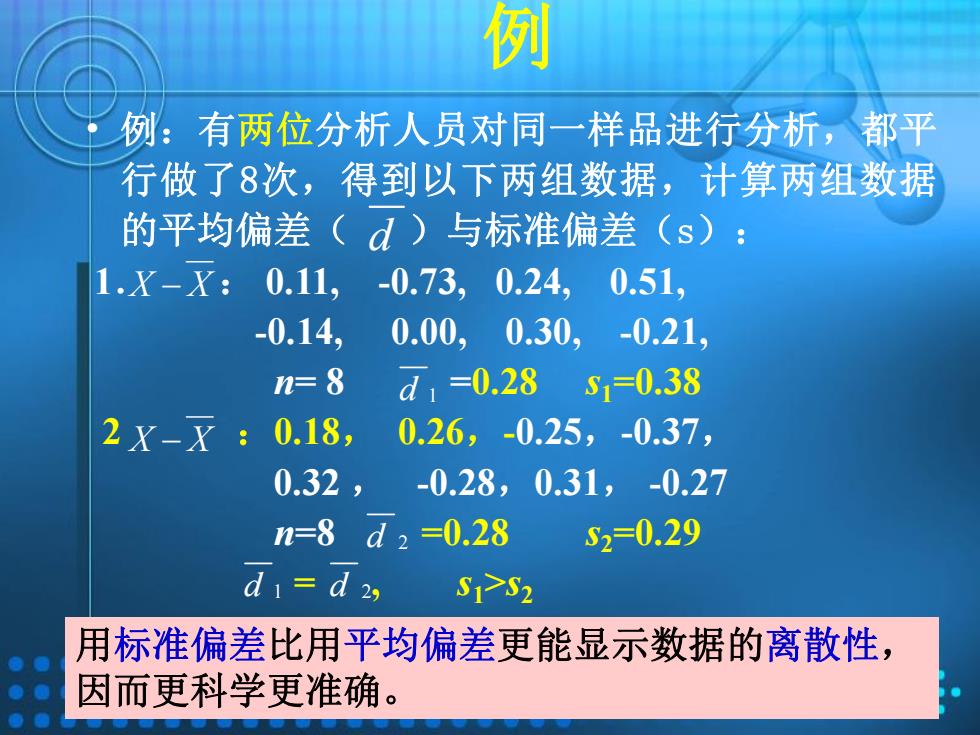
例:有两位分析人员对同一样品进行分析,都平 行做了8次,得到以下两组数据,计算两组数据 的平均偏差(d)与标准偏差(s) 1.X-X: 0.11,-0.73,0.24, 0.51 0.14, 0.00,0.30,-0.21, =8 d10.28 51=0.38 2X-X: 0.18, 0.26,-0.25,-0.37, 0.32, 0.28,0.31,-0.27 n=8d2=0.28 S2=0.29 d1=d2, S17S2 用标准偏差比用平均偏差更能显示数据的离散性, 因而更科学更准确
例 用标准偏差比用平均偏差更能显示数据的离散性, 因而更科学更准确。 • 例:有两位分析人员对同一样品进行分析,都平 行做了8次,得到以下两组数据,计算两组数据 的平均偏差( )与标准偏差(s): 1. : 0.11, -0.73, 0.24, 0.51, -0.14, 0.00, 0.30, -0.21, n= 8 =0.28 s1=0.38 2 :0.18, 0.26,-0.25,-0.37, 0.32 , -0.28,0.31, -0.27 n=8 =0.28 s2=0.29 = , s1>s2 d X X X X d 1 d 2 d 1 d 2

2.随机误差的分布 随机误差(偶然误差)是由一些偶然因 素造成的误差,它的大小和方向难以估 计,似乎没有什么规律,但如果用统计 学方法处理,就会发现它服从一定的统 计规律。为了弄清随机误差的统计规律, 下面我们来讨论以下两个问题。 (1)频数分布 (2)正态分布
2. 随机误差的分布 • 随机误差(偶然误差)是由一些偶然因 素造成的误差,它的大小和方向难以估 计,似乎没有什么规律,但如果用统计 学方法处理,就会发现它服从一定的统 计规律。为了弄清随机误差的统计规律, 下面我们来讨论以下两个问题。 (1)频数分布 (2)正态分布
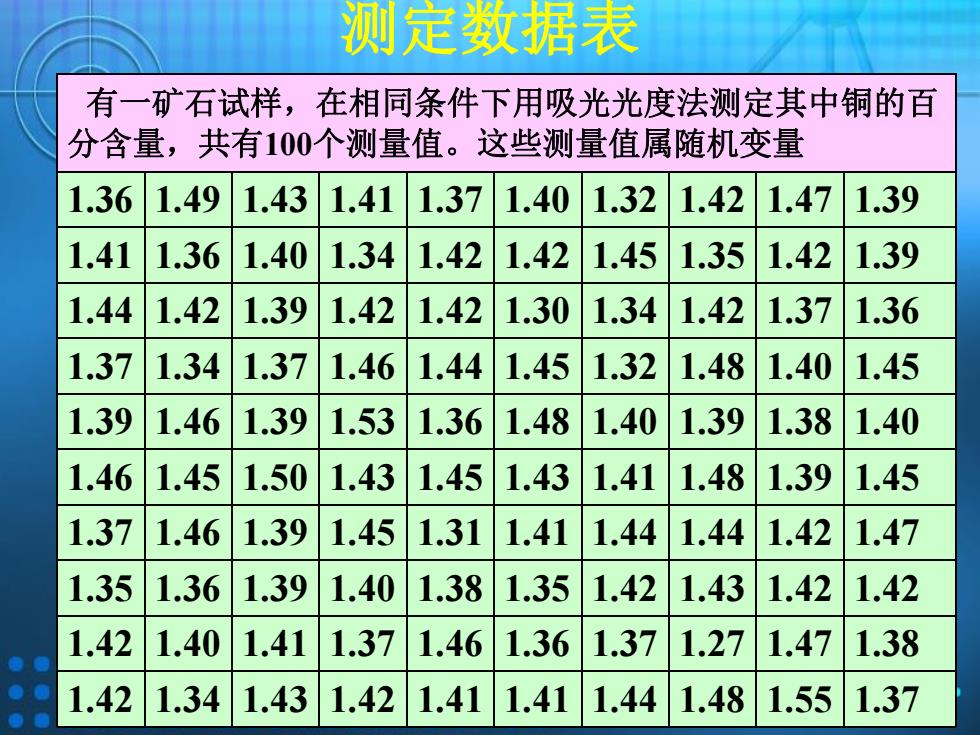
测定数据表 有一矿石试样,在相同条件下用吸光光度法测定其中铜的百 分含量,共有100个测量值。这些测量值属随机变量 1.36 1.49 1.43 1.41 1.37 1.40 1.32 1.42 .47 1.39 1.41 1.36 1.40 1.34 1.42 1.42 1.45 1.35 1.42 1.39 1.44 1.42 1.39 1.42 1.42 1.30 1.34 1.42 1.37 1.36 1.37 1.34 1.37 1.46 1.44 1.45 1.32 1.48 1.40 1.45 1.39 1.46 1.39 1.53 1.36 1.48 1.40 1.39 1.38 1.40 1.46 1.45 1.50 1.43 1.45 1.43 1.41 1.48 1.39 1.45 1.37 1.46 1.39 1.45 1.31 1.41 1.44 1.44 1.42 1.47 1.35 1.36 1.39 1.40 1.38 1.35 1.42 1.43 1.42 1.42 1.42 1.40 1.41 1.37 1.46 1.36 1.37 1.27 1.47 1.38 1.42 1.34 1.43 1.42 1.41 1.41 1.44 1.48 1.55 1.37
测定数据表 有一矿石试样,在相同条件下用吸光光度法测定其中铜的百 分含量,共有100个测量值。这些测量值属随机变量 1.36 1.49 1.43 1.41 1.37 1.40 1.32 1.42 1.47 1.39 1.41 1.36 1.40 1.34 1.42 1.42 1.45 1.35 1.42 1.39 1.44 1.42 1.39 1.42 1.42 1.30 1.34 1.42 1.37 1.36 1.37 1.34 1.37 1.46 1.44 1.45 1.32 1.48 1.40 1.45 1.39 1.46 1.39 1.53 1.36 1.48 1.40 1.39 1.38 1.40 1.46 1.45 1.50 1.43 1.45 1.43 1.41 1.48 1.39 1.45 1.37 1.46 1.39 1.45 1.31 1.41 1.44 1.44 1.42 1.47 1.35 1.36 1.39 1.40 1.38 1.35 1.42 1.43 1.42 1.42 1.42 1.40 1.41 1.37 1.46 1.36 1.37 1.27 1.47 1.38 1.42 1.34 1.43 1.42 1.41 1.41 1.44 1.48 1.55 1.37