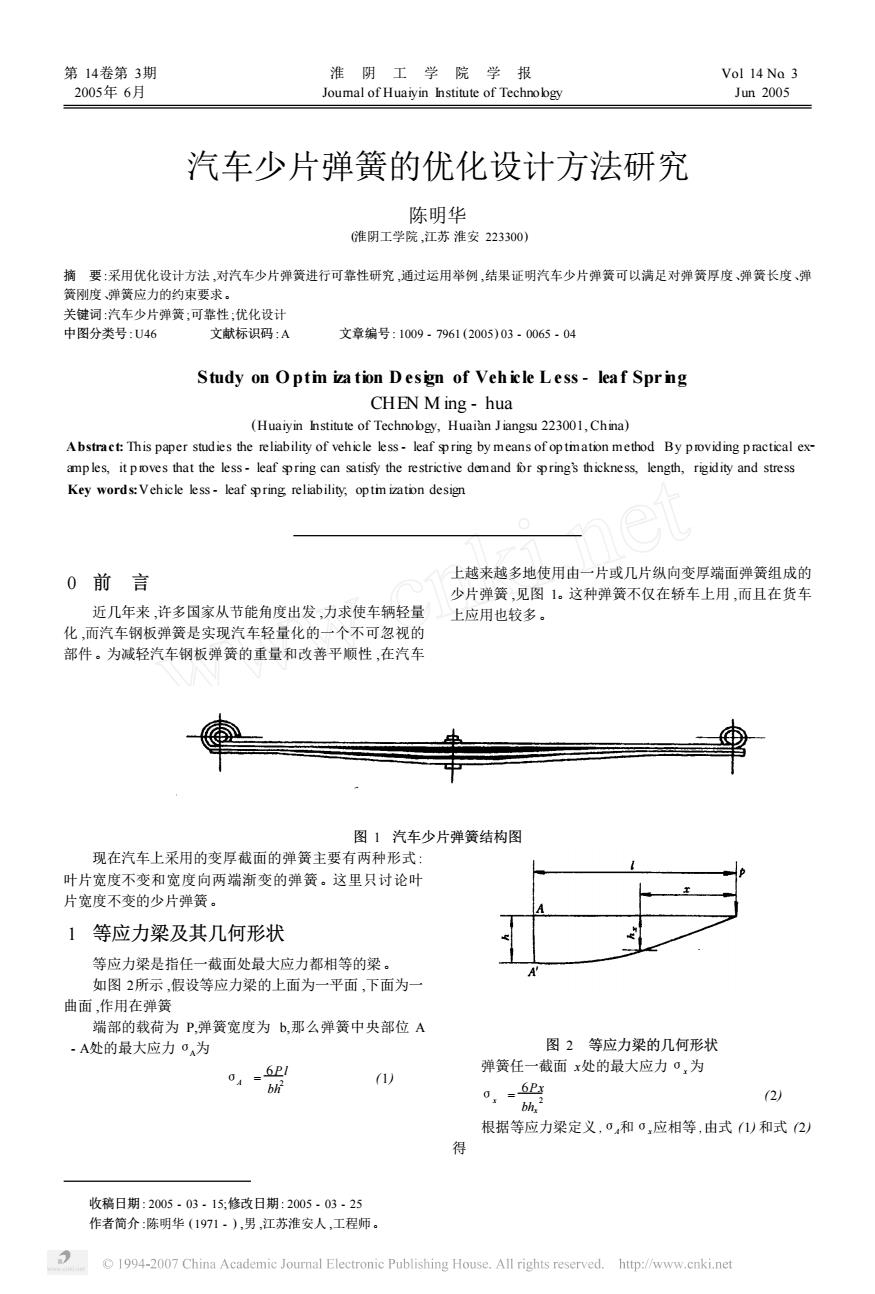
汽车少片弹簧的优化设计方法研究 陈明比 准用工学院,江苏淮安2230 摘委:采用优化设计方法,对汽车少片弹簧进行可靠性研究通过运用举例,结果证明汽车少片弹簧可以满足对弹簧厚度、弹簧长度、弹 文献标识码:A 文章编号:1009.7961(2005)030065.04 Study on Optim ivation Design of Veh icle Less-leaf Spring CHEN M ing-hua 0前言 上越来越多地使用由一片或几片纵向变厚端面弹簧组成的 力求使车 少片弹簧,见图1,这种弹簧不仅在轿车上用,而且在货车 上应用也较多。 可的 部件 为减轻汽车钢板弹簧的重量和 图1汽车少片弹簧结构图 现在汽车上采用的变厚截面的弹簧主要有两种形式: 叶片宽度不变和宽度向两端渐变的弹簧。这里只讨论叶 片宽度不变的少片弹簧。 1等应力梁及其几何形状 曲面,作用在弹 却的 为P,弹簧宽度为b,那么弹簧中央部位A ,A处的最大应力为 图2等应力梁的几何形状 弹簧任一截而x处的最大应力·,为 2 根据等应力梁定义.和,应相等,由式)和式2 收稿日期:2005.03.15:修改日期:2005.03.2 作者简介:陈明华(1971),男江苏淮安人,工程师 1994-2007 China Academie Joumal Electronic Publishing House.All rights reserved.hutp://www.enki.net
汽车少片弹簧的优化设计方法研究 陈明华 (淮阴工学院 ,江苏 淮安 223300) 摘 要 :采用优化设计方法 ,对汽车少片弹簧进行可靠性研究 ,通过运用举例 ,结果证明汽车少片弹簧可以满足对弹簧厚度、弹簧长度、弹 簧刚度、弹簧应力的约束要求。 关键词 :汽车少片弹簧 ;可靠性 ;优化设计 中图分类号 : U46 文献标识码 : A 文章编号 : 1009 - 7961 (2005) 03 - 0065 - 04 Study on O ptim iza tion D esign of Veh icle Less - leaf Spr ing CHEN M ing - hua (Huaiyin Institute of Technology, Huai’an Jiangsu 223001, China) Abstract: This paper studies the reliability of vehicle less - leaf sp ring by means of op timation method. By p roviding p ractical ex2 amp les, it p roves that the less - leaf sp ring can satisfy the restrictive demand for sp ring’s thickness, length, rigidity and stress. Key words:Vehicle less - leaf sp ring; reliability; op tim ization design. 收稿日期 : 2005 - 03 - 15;修改日期 : 2005 - 03 - 25 作者简介 :陈明华 (1971 - ) ,男 ,江苏淮安人 ,工程师。 0 前 言 近几年来 ,许多国家从节能角度出发 ,力求使车辆轻量 化 ,而汽车钢板弹簧是实现汽车轻量化的一个不可忽视的 部件。为减轻汽车钢板弹簧的重量和改善平顺性 ,在汽车 上越来越多地使用由一片或几片纵向变厚端面弹簧组成的 少片弹簧 ,见图 1。这种弹簧不仅在轿车上用 ,而且在货车 上应用也较多。 图 1 汽车少片弹簧结构图 现在汽车上采用的变厚截面的弹簧主要有两种形式 : 叶片宽度不变和宽度向两端渐变的弹簧。这里只讨论叶 片宽度不变的少片弹簧。 1 等应力梁及其几何形状 等应力梁是指任一截面处最大应力都相等的梁。 如图 2所示 ,假设等应力梁的上面为一平面 ,下面为一 曲面 ,作用在弹簧 端部的载荷为 P,弹簧宽度为 b,那么弹簧中央部位 A - A处’ 的最大应力 σA为 σA = 6Pl bh 2 (1) 图 2 等应力梁的几何形状 弹簧任一截面 x处的最大应力 σx 为 σx = 6Px bhx 2 (2) 根据等应力梁定义 ,σA和σx应相等 ,由式 (1) 和式 (2) 得 第 14卷第 3期 淮 阴 工 学 院 学 报 Vol. 14 No. 3 2005年 6月 Journal of Huaiyin Institute of Technology Jun. 2005

656 淮阴工学院学报 2005年 点=h片 3) 式中5为弹密变形修正系数.一般取{-092。 由于梁弯曲变形公式是根据等截面梁推导出来的,用 由式3)可见,等应力梁的厚度沿长度方向按抛物线它计算变截面梁的变形,其结果是近似的:另外,实际生产 规律变化。 的弹簧的截面形状并不是理想的矩形,因此计算弹簧刚度 2抛物线形叶片弹簧 时需要乘以一个经检多正系数。 21 理想的抛物线形弹簧和抛物线形弹簧 3梯形变厚断面弹簧 使用中多用 作用也 线形弹簧,由于这种 的切线BC交于等厚度为 力,因此实际上它是不能使用的要想使其端部能承受切 梯形叶片弹簧ABCD.其中,BC段为梯形变厚度区B段无 应力,则需加强卷耳末端的强度 CD段为等厚度区,统称为梯形变厚新面弹簧简称为梯形 图3为端部加强了的抛物线形叶片弹簧,称之为抛物 弹簧。 线形弹簧。考虑到弹簧的装夹情况.将弹簧的中央和两端。 即图3冲AB段和CD段两部分分别制成相等的厚度.将BC 部分制成按抛物线规律变化的厚度。 图4梯形弹簧 由图4·1所示几何关系可得 图3抛物线形叶片弹簧 当≤x≤时,h-Ax+B.A-(·)/(·4) B=5·)1(· 22抛物线形弹簧的刚度 31 梯形弹簧刚 根据马莫法嘘载荷法)可求出弹簧在载荷作用点处 弹簧在载荷作用点处变形 的变形 s-M, =, 14) 弹簧在任一截面处的惯性矩为 0≤x≤1时J.==八2 4≤≤时,=bax+B)n/2 不相同,分别为 = ,可表示为 4≤x≤5时,小-b城n12-b庄话n/12 将上述各式代入式()进行分段积分,整理后得 4≤x≤时.人-h-b城n/12 8) MM,可表示为 M,=xP.M= 将上述各式代入式4进行分段积分,求得 2娜+0.Ba 1.a) 式中a-416:B-h:Y-aB 当弹簧为对称弹簧.长度为2时,梯形叶片弹簧的刚 式中为弹簧片数」 度为 当弹簧为对称弹簧.长度为2时.利用式5)可求得弹 簧的刚度为 K-23玛 6 32梯形弹簧的最大应力点及最大应力 由图4可见在≤≤6长度范围内,梯形弹簧BC生 1994-007China Academic Joumal Etectrome Publishing House.All rights reserved.http://www.enki.ne
hx = h ( x l ) 1 2 (3) 由式 (3) 可见 ,等应力梁的厚度沿长度方向按抛物线 规律变化。 2 抛物线形叶片弹簧 2. 1 理想的抛物线形弹簧和抛物线形弹簧 从理论上讲 , 将叶片弹簧制造成等应力梁的形式 , 使 弹簧各处最大应力相等是最合理的 ,材料作用也最充分。 一般把按图 2所示抛物线形状制造的叶片弹簧称为理 想的抛物线形弹簧。由于这种弹簧的端部不能承受切应 力 ,因此实际上它是不能使用的。要想使其端部能承受切 应力 ,则需加强卷耳末端的强度。 图 3为端部加强了的抛物线形叶片弹簧 ,称之为抛物 线形弹簧。考虑到弹簧的装夹情况 ,将弹簧的中央和两端 , 即图 3中 AB段和 CD段两部分分别制成相等的厚度 ,将 BC 部分制成按抛物线规律变化的厚度。 图 3 抛物线形叶片弹簧 2. 2 抛物线形弹簧的刚度 根据马莫法 (虚载荷法 ) 可求出弹簧在载荷作用点处 的变形 f = ∫ l 0 M pM l dx EJk (4) 式中 M p、M l分别为由载荷 P和单位力所引起的力矩; JK 为叶片弹簧在任一截面处的惯性矩。 弹簧在不同的长度范围内值各不相同 ,分别为 0 ≤ x ≤ l1 时 , Jx = J1 = bh 3 1 n /12 l1 ≤ x ≤ l2 时 , Jx = bh 3 x n /12 = b ( x l2 ) 3 2 H 3 2 n /12 l2 ≤ x ≤ l时 , Jx = J2 = bh 3 2 n /12 M P、M l可表示为 : M P = xP, M l = x 将上述各式代入式 (4) 进行分段积分 ,求得 f = Pl 3 3EJ2 1 + l2 l 3 k (5) J2 = bh 3 2 n 12 , K = 1 - β3 ,β = h1 / h2 式中 n为弹簧片数。 当弹簧为对称弹簧 ,长度为 2 l时 ,利用式 (5) 可求得弹 簧的刚度为 K = 2 3EJ2 l 3 1 1 + l2 l 3 k ξ (6) 式中 ξ为弹簧变形修正系数 ,一般取 ξ = 0. 92。 由于梁弯曲变形公式是根据等截面梁推导出来的 ,用 它计算变截面梁的变形 ,其结果是近似的;另外 ,实际生产 的弹簧的截面形状并不是理想的矩形。因此计算弹簧刚度 时需要乘以一个经验修正系数 ξ。 3 梯形变厚断面弹簧 由于抛物线形弹簧制造困难 ,因此在实际使用中多用 梯形变厚断面弹簧代替 ,这种叶片弹簧几何形状见图 4。在 图 4中 , BCO’ 为抛物线形状 ,如虚线示。过 B点做抛物线 BC’ 的切线 BC,交于等厚度为 h1 长度为 l1 的端部于点 ,便得到 梯形叶片弹簧 ABCD。其中 , BC段为梯形变厚度区 , AB段和 CD段为等厚度区 ,统称为梯形变厚断面弹簧 ,简称为梯形 弹簧。 图 4 梯形弹簧 由图 4 - 1所示几何关系可得 当 l1 ≤x ≤ l2时 , hx = A x +B, A = ( h2 - h1 ) / ( l2 - l1 ) , B = ( h1 l2 - h2 l1 ) / ( l2 - l1 ) 3. 1 梯形弹簧刚度 弹簧在载荷作用点处变形 f = ∫ l 0 M pM l dx EJx (7) 弹簧在任一截面处的惯性矩 Jx 为 : 0 ≤ x ≤ l1 时 , Jx = J1 = bh 3 1 n /12 l1 ≤ x ≤ l2 时 , Jx = b (A x +B ) 3 n /12 l2 ≤ x ≤ l时 , Jx = J2 = bh 3 2 n /12 M P、M l可表示为 : M P = xP, M l = x 将上述各式代入式 (7) 进行分段积分 ,整理后得 f = Pl 3 3EJ2 1 + l2 l 3 k (8) k =γ3 - 1. 5 (1 - α) 3 (1 - β) 3 2lnβ+4 (1 -β) (1 -γ) (1 -α) + (1 -γ) 2 (1 -β2 ) (1 -α) 2 - 1 (9) 式中 α = l1 / l2 ;β = h1 / h2 ;γ =α/β 当弹簧为对称弹簧 ,长度为 2 l时 ,梯形叶片弹簧的刚 度为 K = 2 3EJ2 l 3 1 1 + l2 l 3 k ξ (10) 3. 2 梯形弹簧的最大应力点及最大应力 由图 4可见 ,在 l1 ≤x ≤ l2长度范围内 ,梯形弹簧 BC长 66 淮 阴 工 学 院 学 报 2005年

第3期 陈明华:汽车少片弹簧的优化设计方法研究 度范围内任意一点厚度均大于抛物线形弹簧上对应点的 41设计变量 厚度因此梯形弹簧在这段上的任一截面的应力均应小于 对于梯形变厚断面弹簧见图5.其设计参数包括·长 抛物线形弹簧上对应点上的应力,又因为抛物线上的各处 度尺寸人{、4.厚度尺寸、M,叶片宽度b及叶片数 应力均相等,且等于B点的应力,所以梯形弹簧BC长度范 围内任一截面上的应力必然小于B点的应力 图4中梯形弹簧BC直线的方程通过切线定义可求得 如果弹簧端部厚度么=A.则利用式11)便可求出 梯形叶片等厚部分的理论长度值 R=128.1 12) 假设梯形叶片的实际等厚部分的长度为《,那么当 图5梯形弹簧的几何形状 ≤(时,梯形叶片在&·4的范围内任一处的应力均小于 4一般取决于弹簧在汽车上的装夹情况,因此是预先 或等于其在B点的应力反之,当4>了时,梯形叶片在变 确定的,即为常数:宽度取决于整车布置和弹簧扁钢的只 厚部分的轮与抛物线相割,使梯形叶片该部分的厚度小 寸规格,在弹簧设计之前可以选定一合适的值:叶片数, 于抛物线形弹簧对应点的厚度。这样梯形叶片变厚部分的 般小于或等于4在优化设计过程中,可以将其作为常数 应力就会大于抛物线叶片对应点的应力,即大于B点处的 因此.优选少片弹簧结构参数时.其设计变量共有4个, 应力 作为连续变量来考虑,即 置,就是 此.可以用式12 梯形弹黄的最大应力点位 应力出 可以看出,当B<05时,即2,<时,弹簧最大应力点就 出现在x<k的范围内 如果弹簧最大应力点不是出现在B点,那么弹簧最大 42目标函数 应力占位置按下述方法确定 以弹簧在理论上所需要的质量最小为日标函数还可 弹密在,≤,≤的区段内任一线面处的量大应力为 以以单位体积内存贮的能量为目标函数),则得到 0,能 FW-pbf西+05x··4)(+)+ 式中p,弹簧材料的密度 43约束条件 对于上式求关于的导数,并令Q则可得弹簧 考虑到弹簧的总体布置、例度、强度、材料、尺寸规格 最大应力点位置 以及制造工艺等方面的要求,可以列出下列约束方程: hg.h x 13) )为确保弹簧卷耳具有足够的强度,弹簧端部等月 部分的厚度,应大于其最小的允许厚度,由此得约束方程 弹簧最大应力为 3X)=·H,≥0 0m=15上4月 (14) 2)为了保证弹簧钢材的淬透性,弹簧中部最大厚度 应限制在某一允许厚度品之内,由此得约束方程 6 不相等,两者之差应大于- 弹簧的受力状 定的前提下头为路低弹的应力应力公有小 )由卷耳的尺寸要求.得约束方程 弹簧质量,一般力求增大等厚部分4的长度但是在加大 后弹簧在4段内的应力可能会过大,所以选择应恰到好 (5)弹簧主片最大伸直长度之半应限制在一允许长度 处, L2之内的弹簧总体布置要求,得约束方程 g.=L2.x.0 4少片变厚断面弹簧尺寸参数优化的数学模型 (6)为保证汽车具有良好的平顺性.弹簧刚度飞对于 设计少片弹簧时 一般是采用试凑法,即根据经验 设计要求的刚度的误差应小于K,由此得约束方程 选尺寸参数,然后代入 式验算 一直到 &=K·:≥0 满足 的要求 为克上述缺点 考虑弹簧的 布和其在区段内的强度,最力 片弹簧进行优化设计 1994-2007 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.enki.ne
度范围内任意一点厚度均大于抛物线形弹簧上对应点的 厚度。因此梯形弹簧在这段上的任一截面的应力均应小于 抛物线形弹簧上对应点上的应力。又因为抛物线上的各处 应力均相等 ,且等于 B 点的应力 ,所以梯形弹簧 BC长度范 围内任一截面上的应力必然小于 B 点的应力。 图 4中梯形弹簧 BC直线的方程通过切线定义可求得 为 hx = 1 2 h2 l2 x + h2 (11) 如果弹簧端部厚度 hx = h1 ,则利用式 (11) 便可求出 梯形叶片等厚部分的理论长度值 l’1 = l2 (2β - 1) (12) 假设梯形叶片的实际等厚部分的长度为 l1 ,那么当 l1 ≤ l’1 时 ,梯形叶片在 l2 - l1 的范围内任一处的应力均小于 或等于其在 B点的应力。反之 ,当 l1 > l’1 时 ,梯形叶片在变 厚部分的轮廓与抛物线相割 ,使梯形叶片该部分的厚度小 于抛物线形弹簧对应点的厚度。这样梯形叶片变厚部分的 应力就会大于抛物线叶片对应点的应力 ,即大于 B 点处的 应力。 因此 ,可以用式 (12) 判断梯形弹簧的最大应力点位 置 ,就是说当 l1 > l’1时 ,弹簧最大应力出现在 x < l2的区间 内;当 l1 ≤ l’1 时 ,最大应力点出现在 B 点。另外 ,由式 (12) 可以看出 ,当β < 0. 5时 ,即 2h1 < h2时 ,弹簧最大应力点就 出现在 x < l2 的范围内。 如果弹簧最大应力点不是出现在 B 点 ,那么弹簧最大 应力点位置按下述方法确定。 弹簧在 l1 ≤x ≤ l2的区段内任一截面处的最大应力为 σA = 6Px bh 2 x n 对于上式求关于 x的导数 ,并令 dσx dx = 0,则可得弹簧 最大应力点位置 x = h1 l2 - h2 l1 h2 - h1 (13) 弹簧最大应力为 σm ax = 1. 5 P xbn ( l2 - l1 h2 - h1 ) 2 (14) 在设计少片弹簧时 , 除了要计算弹簧的最大应力点 外 ,还须校核弹簧在弹簧夹处的应力。因为一般变厚截面 的弹簧近似于等应力梁 , 各处应力相差很少 , 而弹簧夹对 弹簧的受力状态会产生一定的影响。另外 , 在弹簧刚度确 定的前提下 ,为降低弹簧的应力、改善其应力分布及减小 弹簧质量 ,一般力求增大等厚部分 l1的长度。但是在加大 l1 后弹簧在 l1 段内的应力可能会过大 , 所以选择应恰到好 处。 4 少片变厚断面弹簧尺寸参数优化的数学模型 设计少片弹簧时 , 一般是采用试凑法 , 即根据经验补 选尺寸参数 ,然后代入公式验算 ,经过几轮反复 ,一直到选 择的参数能满足刚度和强度的要求为止。这种设计方法不 容易获得最佳的设计方案 ,且费工时。为克服上述缺点 ,可 按优化方法对少片弹簧进行优化设计。 4. 1 设计变量 对于梯形变厚断面弹簧 ,见图 5,其设计参数包括 :长 度尺寸 l、l1、l3 ,厚度尺寸 h1、h2 ,叶片宽度 b及叶片数 n。 图 5 梯形弹簧的几何形状 l3 一般取决于弹簧在汽车上的装夹情况 ,因此是预先 确定的 ,即为常数; 宽度取决于整车布置和弹簧扁钢的尺 寸规格 ,在弹簧设计之前可以选定一合适的值;叶片数 n一 般小于或等于 4,在优化设计过程中 ,可以将其作为常数。 因此 ,优选少片弹簧结构参数时 ,其设计变量共有 4个 ,并 作为连续变量来考虑 ,即 X = x1 x2 x3 x4 = h1 h2 l1 l 4. 2 目标函数 以弹簧在理论上所需要的质量最小为目标函数 (还可 以以单位体积内存贮的能量为目标函数 ) ,则得到 F (X) =ρbn x1 x3 + 0. 5 ( x4 - x3 - l3 ) ( x1 + x2 ) + x2 l3 式中 ρ- 弹簧材料的密度。 4. 3 约束条件 考虑到弹簧的总体布置、刚度、强度、材料、尺寸规格 以及制造工艺等方面的要求 ,可以列出下列约束方程 : (1) 为确保弹簧卷耳具有足够的强度 ,弹簧端部等厚 部分的厚度 h1 应大于其最小的允许厚度 ,由此得约束方程 g1 (X) = x1 - H1 ≥ 0 (2) 为了保证弹簧钢材的淬透性 ,弹簧中部最大厚度 x2 应限制在某一允许厚度 H2 之内 ,由此得约束方程 g2 (X) = H2 - x2 ≥ 0 (3) 根据弹簧厚度和不相等 ,两者之差应大于 H12 = 0. 1cm 的要求 ,得约束方程 g3 (X) = x2 - x1 - H12 ≥ 0 (4) 由卷耳的尺寸要求 ,得约束方程 g4 (X) = x3 ≥ 0 (5) 弹簧主片最大伸直长度之半应限制在一允许长度 L /2之内的弹簧总体布置要求 ,得约束方程 g5 (X) = L /2 - x4 ≥ 0 (6) 为保证汽车具有良好的平顺性 ,弹簧刚度 Kh 对于 设计要求的刚度的误差应小于 Kg ,由此得约束方程 g6 (X) = Ke - K - Kh Kh ≥ 0 (7) 考虑弹簧的应力分布和其在区段内的强度 ,最大 应小于允许应力 [σ]1 ,由此得约束方程 第 3期 陈明华 :汽车少片弹簧的优化设计方法研究 67

68 淮阴工学院学报 2005年 方程(4)(5)是对弹窑长度的的束要求约束方程6 是对弹簧刚度的的束要求.约束方程(7)~(8)是对弹蜀 (⑧)按弹簧强度要求,弹簧在我荷的作用下,其计算应 应力的约束要求 力应小于材料的允许应力上。 首先用式4·6)判断出弹簧最大应力位置.然后计算 5计算实例 其最大应力,即 作用在弹簧上的载荷P=4925N,弹簧宽度b=7 6am,最大允许伸直长度之半L2-75m,中部等厚部分长 度与”50m 端部等厚最小允许厚度一Q8a 允许度 「2≥0 用应力 设计变量的上 和下限 当≤时 采用复合形法在计算机上进行随机搜索和迭代,取项 am-Ph.:山≥0 点数为8各项点函数最小点的均方根值6一103.计算列 约束方程~是对弹簧厚度的约束要求.约束 簧取不同片数时的优化结构参数列于表1。 表1 弹簧取不同片数时的优化结构参数 为h 月x=h .= F(X 6 N MPa /(N/am) 00105 119348 1172825 6á47935 30 41988 1267 8131 1379 149237 617576 由表6.1可以看出,弹簧为2片时,满足不了给定的 1996 条件,即无解:取4片时,虽然能满足给定的条件,但其质量 :机械工业出 F(X)不是最小;取3片时,既能满足给定的约束条件,又能 使弹簧获得最小质量,因此片数取3时的结构参数便为本 制造.1999.(6):32.31 琴安侧的优化设计销果 [6历耀青.最优化计算方法常用程序汇编M)北京:工人出 版杜.200 1邓城黄洪钟多目标模糊优化的数学模型及其求解原理 未生.结构有限元动态模型修正方法综述振动与冲 和方法U1机候设计与研究,1996,() 【8陈家瑞汽车构造M)北京:人民交通出版社,201 (责任编辑:蒋华) 007China Academie Joum Eletron Publishing House.All rightsresrved.hp://ww.cnki
g7 (X) = [σ]1 - 6Px3 nbx 2 1 ≥ 0 (8) 按弹簧强度要求 ,弹簧在载荷的作用下 ,其计算应 力应小于材料的允许应力 [σ]2。 首先用式 (4 - 6) 判断出弹簧最大应力位置 ,然后计算 其最大应力 ,即 当 x3 > ( x4 - l3 ) 2 x1 x2 - 1 时 g8 (X) = [σ]2 - 1. 5 P ( x2 - x1 ) nb[ x1 ( x4 - l3 ) - x2 x3 ] ( x4 - l3 ) - x3 x2 - x1 2 ≥ 0 当 x3 ≤ ( x4 - l3 ) 2 x1 x2 - 1 时 g8 (X) = [σ]2 - 6P ( x4 - l3 ) nbx2 ≥ 0 约束方程 (1) ~ (3) 是对弹簧厚度的约束要求 ,约束 方程 (4) ~ (5) 是对弹簧长度的约束要求 ,约束方程 (6) 是对弹簧刚度的约束要求 ,约束方程 (7) ~ (8) 是对弹簧 应力的约束要求。 5 计算实例 作用在弹簧上的载荷 P = 4925N, 弹簧宽度 b = 7. 6cm ,最大允许伸直长度之半 L /2 = 75cm ,中部等厚部分长 度 l3 = 5cm , 端 部 等 厚 最 小 允 许 厚 度 H1 = 0. 8cm , 55S iM nVB弹簧材料的最大允许淬透厚度 H2 = 1. 5cm,设计 要求的刚度 Kh = 1260N / cm,允许刚度误差 Ke = 0. 008,许 用应力 [σ]1 = 300M Pa, [σ]2 = 420M Pa,设计变量的上限 和下限为 0. 8 ≤x1 ≤1. 5, 0. 8 ≤x2 ≤1. 5, 5 ≤x3 ≤20, 60 ≤ x4 ≤ 75。 采用复合形法在计算机上进行随机搜索和迭代。取顶 点数为 8,各项点函数最小点的均方根值 ε = 10 - 3 ,计算弹 簧取不同片数时的优化结构参数列于表 1。 表 1 弹簧取不同片数时的优化结构参数 片数 n x1 = h1 / cm 〗x2 = h2 / cm x3 = l1 / cm x4 = l / cm F (X) /N σx /MPa K / (N / cm) 4 3 0. 80195 0. 81311 1. 19343 1. 37909 11. 72825 14. 92377 66. 47935 66. 17576 308 248 419. 88 420 1267 1269 2 无 解 由表 6 - 1可以看出 ,弹簧为 2片时 ,满足不了给定的 条件 ,即无解 ;取 4片时 ,虽然能满足给定的条件 ,但其质量 F (X)不是最小 ;取 3片时 ,既能满足给定的约束条件 ,又能 使弹簧获得最小质量 ,因此片数取 3时的结构参数便为本 计算实例的优化设计结果。 参考文献 : [ 1 ]邓斌 ,黄洪钟. 多目标模糊优化的数学模型及其求解原理 和方法 [J ]. 机械设计与研究 , 1996, (1) [ 2 ]孙靖民. 机械优化设计 [M ]. 北京 :机械工业出版社 , 1997 [ 3 ]刘惟信. 机械可靠性设计 [M ]. 北京 :清华大学出版社 , 1996 [ 4 ]庞士宗 ,产品数据管理 [M ]. 北京 :机械工业出版社 , 2000. [ 5 ]张红兵. 有限元模型中螺栓的温度法模拟 [J ]. 机械设计与 制造. 1999, (6) : 32 - 33. [ 6 ]万耀青. 最优化计算方法常用程序汇编 [M ]. 北京 :工人出 版社. 2000. [ 7 ]魏来生. 结构有限元动态模型修正方法综述 [J ]. 振动与冲 击 , 1998, 17 (3) : 44 - 46. [8 ]陈家瑞.汽车构造 [M ].北京:人民交通出版社 , 2001. (责任编辑 :蒋 华 ) 68 淮 阴 工 学 院 学 报 2005年