
“十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 少本理王大到 第2章几何元素的投影 2.1点的投影 2.2直线的投影 2.3平面的投影 2.4直线与平面、平面与平面的相对位置 2.5投影变换 2.6综合问题解题示例
1 第2章 几何元素的投影 2.1 点的投影 2.2 直线的投影 2.3 平面的投影 2.4 直线与平面、平面与平面的相对位置 2.5 投影变换 2.6 综合问题解题示例

十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 山东用王大家 2.6综合问题解题示例 2.6.1解题的一般步骤 ★ 分析题意 nn■a■a■aaa000naaa1■a01 BERNBEEn00nn ★ 确定解题的方法和步骤 ★投影作图 2.6.2 题目分类及分析方法 题目分类:相对位置题、距离题、角度题、综合题 分析方法 相对位置题:轨迹法和逆推法。 距离题(定距离和等距离):轨迹法。 角度题:直角定理的应用。 综合题:轨迹法、逆推法、多种辅助方法
2 2.6 综合问题解题示例 2.6.1 解题的一般步骤 ★ 分析题意 ★ 确定解题的方法和步骤 ★ 投影作图 题目分类:相对位置题、距离题、角度题、综合题 2.6.2 题目分类及分析方法 分析方法 相对位置题:轨迹法和逆推法。 距离题(定距离和等距离):轨迹法。 角度题:直角定理的应用。 综合题:轨迹法、逆推法、多种辅助方法
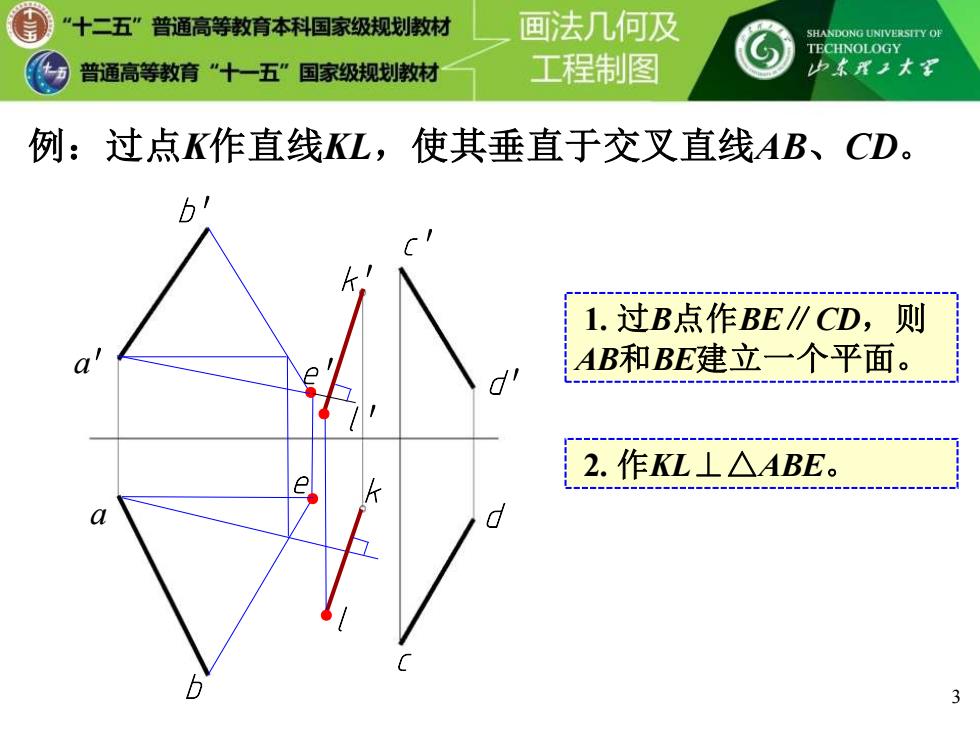
“十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 山本理王大到 例:过点K作直线KL,使其垂直于交叉直线AB、CD。 1.过B点作BE∥CD,则 a AB和BE建立一个平面。 2.作KL⊥△ABE
b′ c′ d′ k′ a′ b c d k a 3 例:过点K作直线KL,使其垂直于交叉直线AB、CD。 e ● e ● ′ 1. 过B点作BE∥CD,则 AB和BE建立一个平面。 2. 作KL⊥△ABE。 ●l ● l′
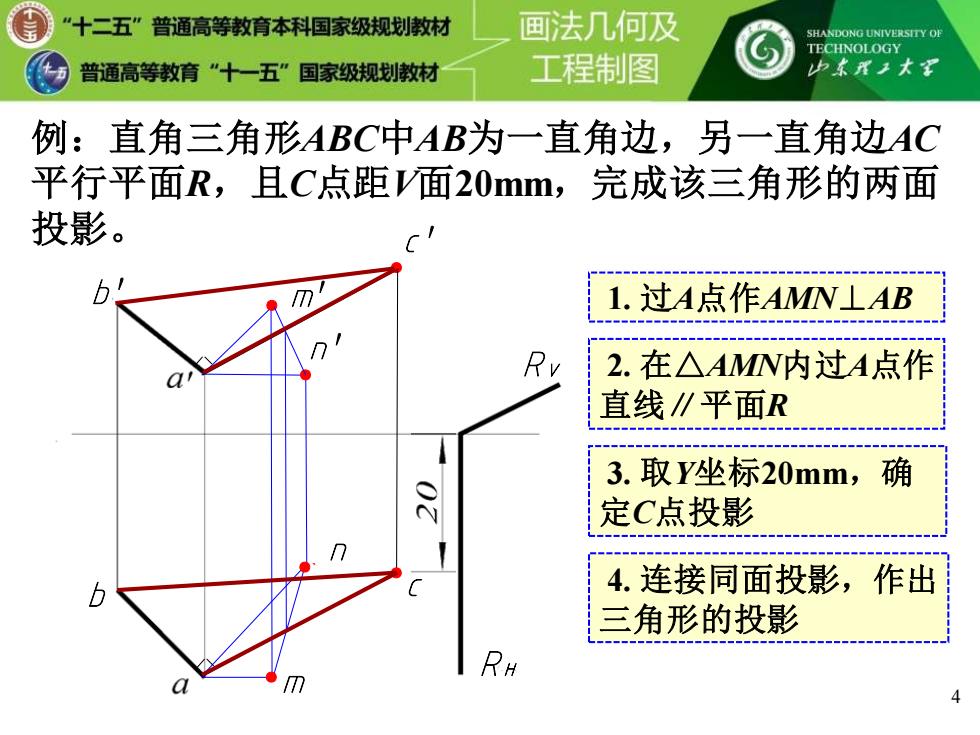
十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 例:直角三角形ABC中AB为一直角边,另一直角边AC 平行平面R,且C点距V面20mm,完成该三角形的两面 投影。 1.过A点作AMN⊥AB Rv 2.在△AMN内过A点作 直线∥平面R 3.取Y坐标20mm, 确 定C点投影 4.连接同面投影,作出 三角形的投影 RH
b′ b RH RV 4 例:直角三角形ABC中AB为一直角边,另一直角边AC 平行平面R,且C点距V面20mm,完成该三角形的两面 投影。 c′ ● 1. 过A点作AMN⊥AB 2. 在△AMN内过A点作 直线∥平面R c ● ●m ● m′ ●` n n′ ● 3. 取Y坐标20mm,确 定C点投影 4. 连接同面投影,作出 三角形的投影
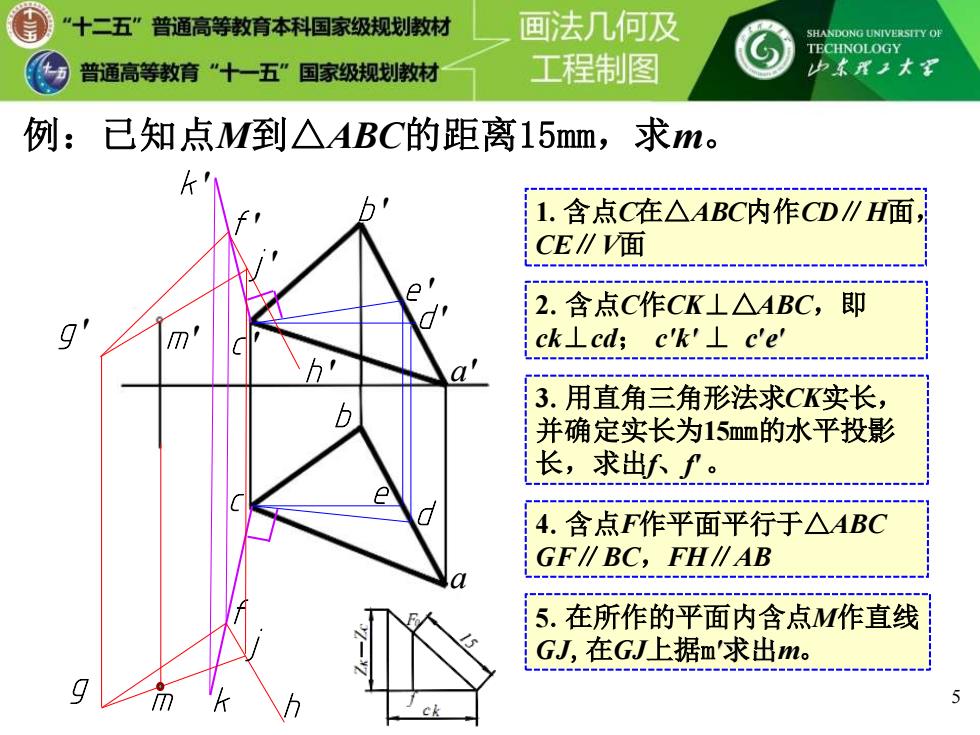
“十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 少本X王大到 例:已知点M到△ABC的距离15mm, 求m。 1.含点C在△ABC内作CD∥H面, CE∥V面 2.含点C作CK⊥△ABC,即 ck⊥cd;c'k'⊥c'e' 3.用直角三角形法求CK实长, 并确定实长为15mm的水平投影 长,求出f。 4.含点F作平面平行于△ABC GF∥BC,FH∥AB 5.在所作的平面内含点M作直线 GJ,在GJ上据m'求出m。 5 ck
m′ a′ b′ c′ a b c 4.含点F作平面平行于△ABC GF∥BC,FH∥AB 5 2.含点C作CK⊥△ABC,即 ck⊥cd; c′k′ ⊥ c′e′ 1.含点C在△ABC内作CD∥H面, CE∥V面 3.用直角三角形法求CK实长, 并确定实长为15mm的水平投影 长,求出f、f′ 。 5.在所作的平面内含点M作直线 GJ,在GJ上据m′求出m。 d′ d e e′ k k′ g′ f f′ g h′ h j′ j m 例:已知点M到△ABC的距离15mm,求m