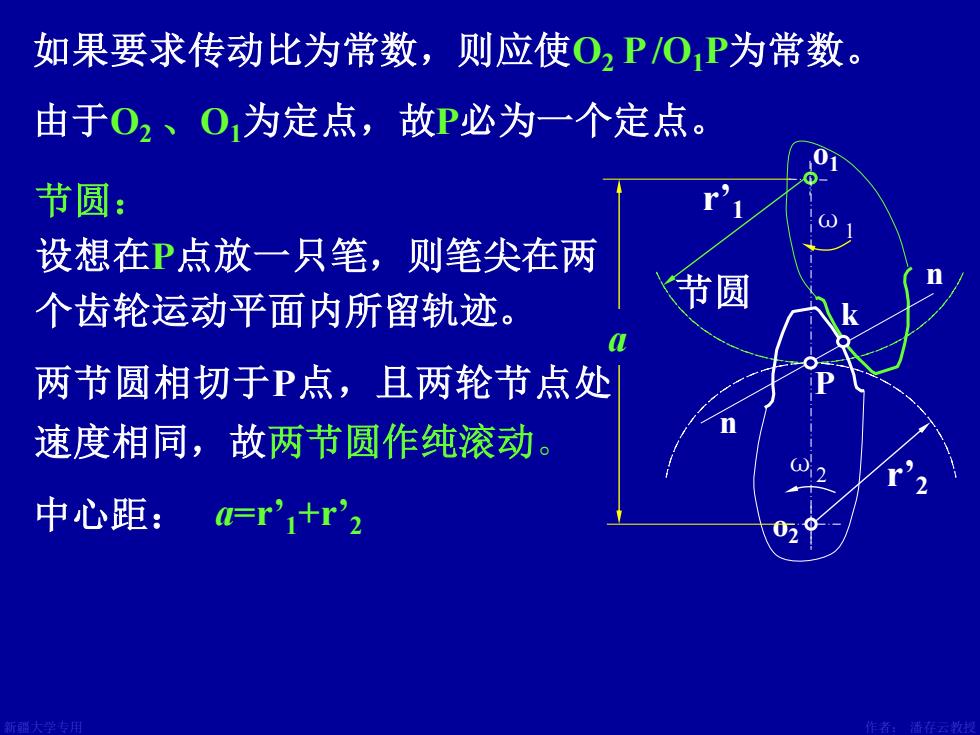
如果要求传动比为常数,则应使O2POP为常数。 由于O2、O1为定点,故P必为一个定点。 节圆: 设想在P点放一只笔,则笔尖在两 个齿轮运动平面内所留轨迹。 节圆 两节圆相切于P点,且两轮节点处 速度相同,故两节圆作纯滚动。 中心距:=r’1+r’2
新疆大学专用 作者: 潘存云教授 设计:潘存云 节圆 如果要求传动比为常数,则应使O2 P/O1P为常数。 节圆: 设想在P点放一只笔,则笔尖在两 个齿轮运动平面内所留轨迹。 由于O2 、O1为定点,故P必为一个定点。 两节圆相切于P点,且两轮节点处 速度相同,故两节圆作纯滚动。 r’1 r’2 a=r’1+r’ 中心距: 2 o1 ω1 n n P o2 ω2 k a

2.齿廓曲线的选择 理论上,满足齿廓啮合定律的曲线有无穷多,但考 虑到便于制造和检测等因素,工程上只有极少数几种 曲线可作为齿廓曲线,如渐开线、其中应用最广的是 渐开线,其次是摆线(仅用于钟表)和变态摆线(摆线针 轮减速器),近年来提出了圆弧和抛物线。 渐开线齿廓的提出已有近两百多年的历史,目前还 没有其它曲线可以替代。主要在于它具有很好的传动 性能,而且便于制造、安装、测量和互换使用等优点。 本章只研究渐开线齿轮。 作者:云
新疆大学专用 作者: 潘存云教授 2.齿廓曲线的选择 理论上,满足齿廓啮合定律的曲线有无穷多,但考 虑到便于制造和检测等因素,工程上只有极少数几种 曲线可作为齿廓曲线,如渐开线、其中应用最广的是 渐开线,其次是摆线(仅用于钟表)和变态摆线 (摆线针 轮减速器),近年来提出了圆弧和抛物线。 渐开线齿廓的提出已有近两百多年的历史,目前还 没有其它曲线可以替代。主要在于它具有很好的传动 性能,而且便于制造、安装、测量和互换使用等优点。 本章只研究渐开线齿轮
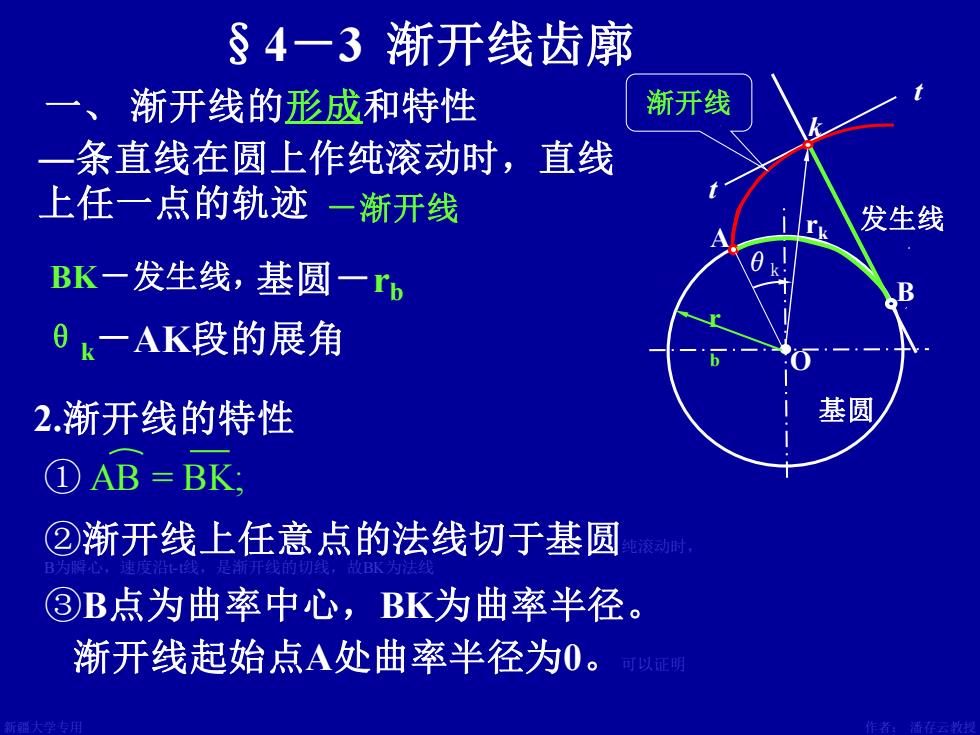
§4一3渐开线齿廓 一、渐开线的形成和特性 渐开线 一条直线在圆上作纯滚动时,直线 上任一点的轨迹一渐开线 发生线 BK一发生线,基圆一r 8 一AK段的展角 2.渐开线的特性 基圆 ①AB=BK, ②渐开线上任意点的法线切于基圆 ③B点为曲率中心,BK为曲率半径。 渐开线起始点A处曲率半径为0。 可以证明
新疆大学专用 作者: 潘存云教授 设计:潘存云 §4-3 渐开线齿廓 一、 渐开线的形成和特性 ―条直线在圆上作纯滚动时,直线 上任一点的轨迹 2.渐开线的特性 ②渐开线上任意点的法线切于基圆纯滚动时, B为瞬心,速度沿t-t线,是渐开线的切线,故BK为法线 ③B点为曲率中心,BK为曲率半径。 渐开线起始点A处曲率半径为0。可以证明 BK-发生线, ① AB = BK; t t 发生线 B k 基圆 O A rk 基圆- θk rb θk-AK段的展角 -渐开线 渐开线 r b

定义:啮合时K点正压力方向与速度方向 所夹锐角为渐开线上该点之压力角xk。 rp=rk cos ak ④离中心越远,渐开线上的压力角越大。 ⑤渐开线形状取决于基圆 当rb→∞,变成直线。 ⑥基圆内无渐开线。 ⑦同一基圆上任意两条渐开 线公法线处处相等
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 O A B k A1 B1 o1 θk K ⑤渐开线形状取决于基圆 ⑥基圆内无渐开线。 ⑦同一基圆上任意两条渐开 线公法线处处相等。 当rb→∞,变成直线。 rk θk αk αk vk ④离中心越远,渐开线上的压力角越大。 rb 定义:啮合时K点正压力方向与速度方向 所夹锐角为渐开线上该点之压力角αk。 rb=rk cosαk B3 o3 θk A2 B2 o2

⑦同一基圆上任意两条渐开线的公法线处处相等。 两条反向渐开线,由性质①和②有: AB=ANI+N B=AINI+NiBI =AiB AB=AN2 N2B =A2N2 N2B2 =A2B2 ∴.AB1=A2B2 两条同向渐开线: A1E1=A2E2 BIE1=A1E1-ABI BE1=B2E2 B2E2=A2E2一A2B2 顺口溜: 弧长等于发生线, 基圆切线是法线, 曲线形状随基圆, 基圆内无渐开线
新疆大学专用 作者: 潘存云教授 设计:潘存云B C’ A C rb O E C” ⑦同一基圆上任意两条渐开线的公法线处处相等。 两条反向渐开线, 由性质①和②有: 两条同向渐开线: B1E1 = A1E1-A1B1 B2E2 = A2E2-A2B2 B1E1 = B2E2 ∴ A1B1 = A2B2 A1E1 = A2E2 AB = AN1 + N1B = A1N1 + N1B1 = A1B1 AB = AN2 + N2B = A2N2 + N2B2 = A2B2 A1 B1 N1 A2 B2 N2 顺口溜: 弧长等于发生线, 基圆切线是法线, 曲线形状随基圆, 基圆内无渐开线。 E2 E1