
显著性检验 ◆如果大概率事件和小概率事件有两个分界,这种类型称 为“双侧检验”(two-sided/two-tailed test) 实例:平均值是否显著异于参考值一可能“大于” 也可能“小于” ◆如果大概率事件和小概率事件只有一个分界,这种类型 称为“单侧检验”(one-sided/one-tailed test) 实例:平均值是否显著大于(小于)参考值
显著性检验 ◆ 如果大概率事件和小概率事件只有一个分界,这种类型 称为“单侧检验”(one-sided/one-tailed test) 实例:平均值是否显著大于(小于)参考值 ◆ 如果大概率事件和小概率事件有两个分界,这种类型称 为“双侧检验”(two-sided/two-tailed test) 实例:平均值是否显著异于参考值——可能“大于” 也可能“小于

双侧检验图示 大概率(1-a四事件的发生范围.a2, 面积1-a x。随机变量的取值如果出现在此 范围,说明其在统计意义上不显著。 面积 /2 小概率()事件的发生范围 0,.a2]Ua2,o).随机变量的取值 如果出现在此范围,说明其在统计意 义上显著。 X1.a2 Xa2 随机变量 例如,两组数据的精密度是否显著不同
双侧检验图示 例如,两组数据的精密度是否显著不同

右侧单侧检验图示 大概率(1一)事件的发生范围0, 面积1,a x。随机变量的取值如果出现在此 范围,说明其在统计意义上不显著。 面积a 0 小概率()事件的发生范围代a)。 随机变量的取值如果出现在此范 围,说明其在统计意义上显著。 Xa 随机变量 例如,一组数据的精密度是否比另一组显著地差 方差 大
右侧单侧检验图示 例如,一组数据的精密度是否比另一组显著地差 方差 大
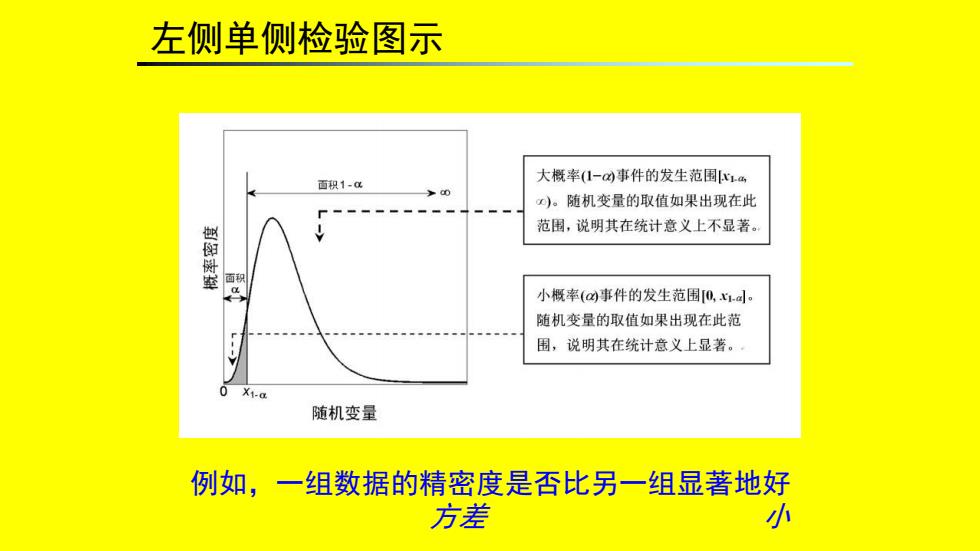
左侧单侧检验图示 百积1- 大概率(1-四事件的发生范围1m )。随机变量的取值如果出现在此 范围,说明其在统计意义上不显著。 面9 小概率(a四事件的发生范围0,d。 随机变量的取值如果出现在此范 围,说明其在统计意义上显著。 随机变量 例如,一组数据的精密度是否比另一组显著地好 方差 小外
左侧单侧检验图示 例如,一组数据的精密度是否比另一组显著地好 方差 小

显著性检验的P值 P.值(P-value)是当原假设为真时,出现比观测 值更加极端的结果的概率。P值与显著性水平Q 具有相同的涵义,所以也被称为“观测到的显著性 水平”。(详细解释参见教材34页) P值与显著性水平α的比较是显著性检验的一种 判别方式;另一种方式是检验统计量的取值(对应 于P-值)与临界值(对应于a)的比较。 第二种方式很经典;第一种方式很简单(因为统计 软件会给出P-值,计算方法参见教材34页)
显著性检验的 P-值 P-值(P-value)是当原假设为真时,出现比观测 值更加极端的结果的概率。P-值与显著性水平 α 具有相同的涵义,所以也被称为“观测到的显著性 水平”。(详细解释参见教材 34 页) P-值与显著性水平 α 的比较是显著性检验的一种 判别方式;另一种方式是检验统计量的取值(对应 于P-值)与临界值(对应于 α)的比较。 第二种方式很经典;第一种方式很简单(因为统计 软件会给出P-值,计算方法参见教材 34 页)