
Utility of the Density of States With N(E)we can immediately 「N(E)EdE calculate the average energy per (E〉= total energy 0 electron in the 3-D FEG system: electrons N(E)dE We can simplify by using the N(E)=CE12 relation: 2 EF N(E) C∫EndE E5/2 5 (E〉= 0 0 3 E 2 C E2 dE E32 3 Er Why the factor 3/5?Alook at the density of states curve should give the answer:
Utility of the Density of States We can simplify by using the relation: With N(E) we can immediately calculate the average energy per electron in the 3-D FEG system: Why the factor 3/5? A look at the density of states curve should give the answer: = = F F E E N E dE N E E dE electrons total energy E 0 0 ( ) ( ) # 1/ 2 N(E) = CE E F E E E E E E C E dE C E dE E F F F F 5 3 3 2 5 2 0 3/ 2 0 5/ 2 0 1/ 2 0 3/ 2 = = = N(E) E EF
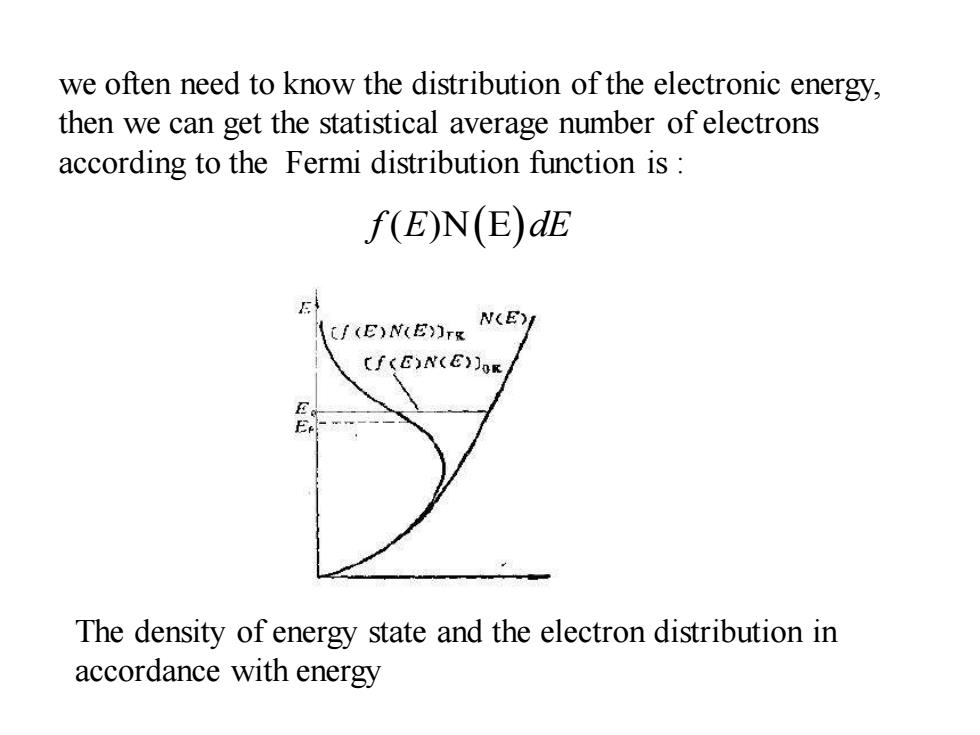
we often need to know the distribution of the electronic energy, then we can get the statistical average number of electrons according to the Fermi distribution function is: f(E)N(E)dE N(E) (E)N(E)rg Cf(E)N(E)JoR The density of energy state and the electron distribution in accordance with energy
The density of energy state and the electron distribution in accordance with energyf E dE ( )N E( ) we often need to know the distribution of the electronic energy, then we can get the statistical average number of electrons according to the Fermi distribution function is :

Determination of Er In the system,the total number of electron is given by N=f(E)N(E)dE Introducing a new function (E)=fN(E)dE Q(E)means the total number of the quantum states with energy above E. Then we can obtain N-E5)) Because Q(E)=0 when E-0,and f(E)-0 when E=oo,The first is zero.So af dE
Determination of EF ( ) 0 N f E dE ( )N E = ( ) 0 ( ) N E E Q E dE = 0 ( ) ( ) ( ) 0 N f E Q E Q E dE f E + = − In the system , the total number of electron is given by 0 N Q E( ) E E f d = − Introducing a new function Because Q(E) =0 when E=0, and f (E)=0 when E=∞, The first is zero. So Q (E) means the total number of the quantum states with energy above E. Then we can obtain