§15-5驻波(Standing Wave) 一)何谓驻波 两列振幅相同的相干波在同一直线上沿相反 方向传播彼此相遇叠加而形成的波。 电动音叉 腹 点 二) 驻波分析 1)波形曲线分析
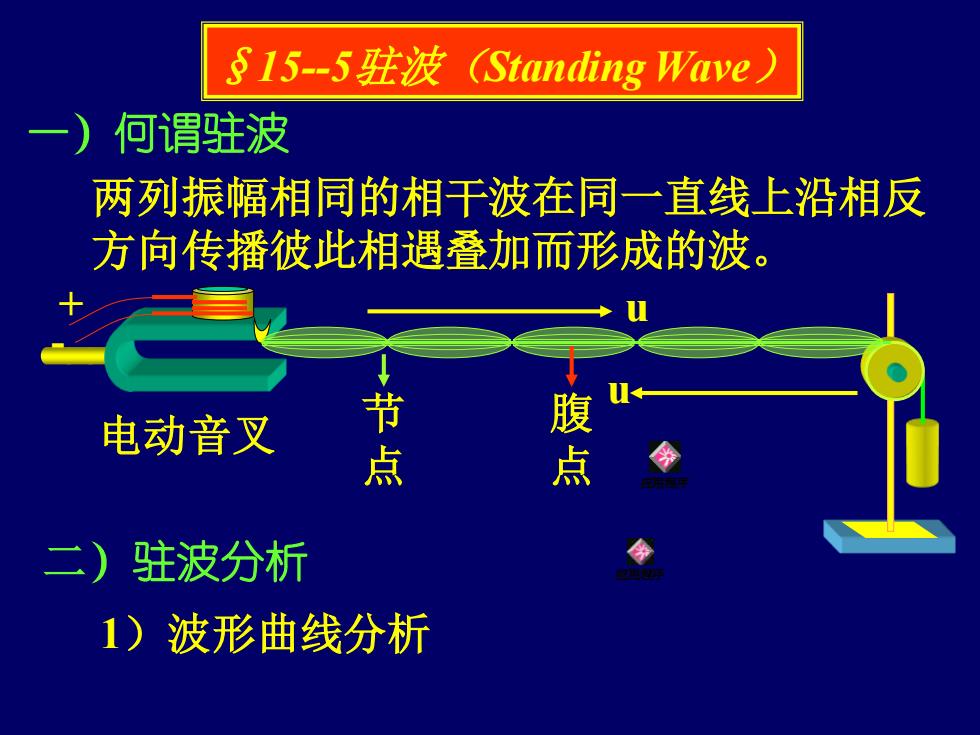
§15-5驻波(Standing Wave) 一)何谓驻波 两列振幅相同的相干波在同一直线上沿相反 方向传播彼此相遇叠加而形成的波。 u u 节 点 二)驻波分析 1)波形曲线分析 电动音叉 + - 腹 点

节 点 腹点
X Y 节点 腹点
/2 . -λ/2- 4 由此可见,驻波特点是: 1)驻波波形固定,有波腹点和波节点,且相邻 的腹点与腹点,节点与节点间距离为入/2 相邻的节点与腹点间的距离为入/4 2)相邻两节点间的质点具有相同的位相,节点 两侧具有相反的位相
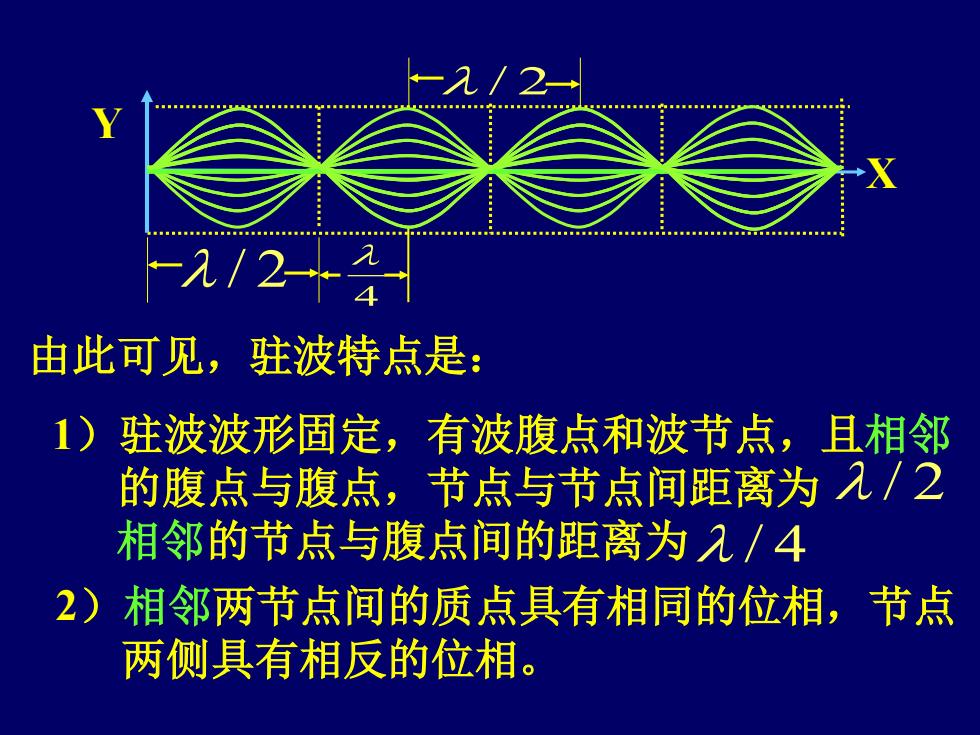
由此可见,驻波特点是: 2)相邻两节点间的质点具有相同的位相,节点 两侧具有相反的位相。 1)驻波波形固定,有波腹点和波节点,且相邻 的腹点与腹点,节点与节点间距离为 / 2 相邻的节点与腹点间的距离为 / 4 X Y / 2 / 2 4
2)数学分析: y Aco2r(v-*) y2=Acos2π(M+ x一元 y=y+Y2 =Acos2r0t-克+1eos2xi+克 由: cosa+cos$=2cos a+B cos -B 得: 2 2 y=(2Acos2z )cos2ru 驻波方程
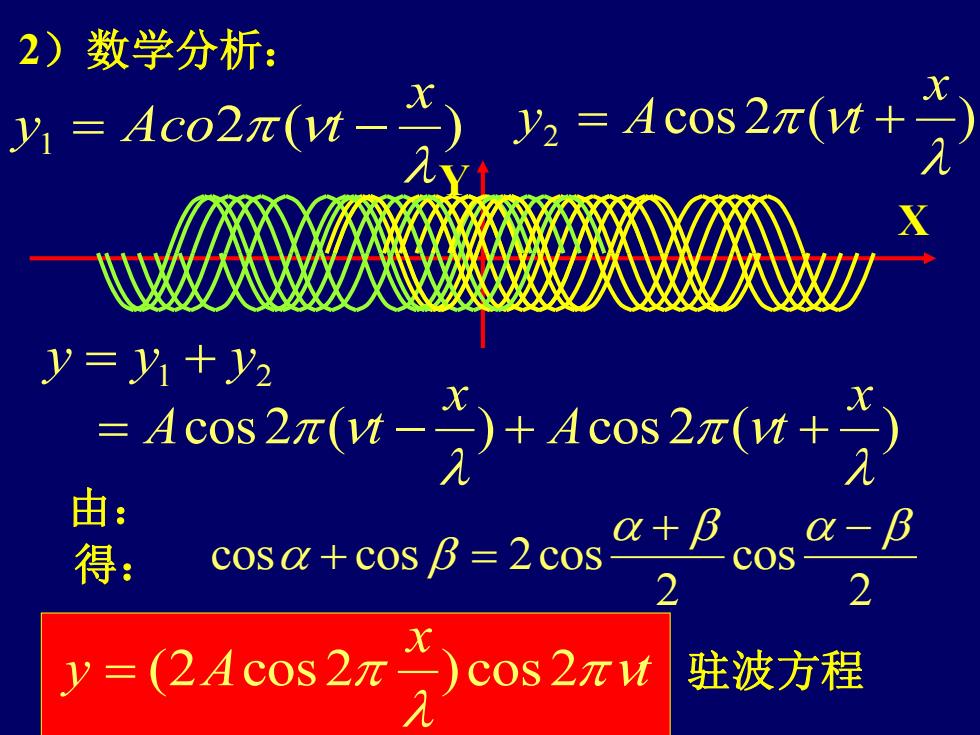
2)数学分析: X Y 2 ( ) 1 x y = Aco t − cos 2 ( ) 2 x y = A t + cos 2 ( ) cos 2 ( ) x A t x = A t − + + 1 2 y = y + y t x y A = (2 cos 2 ) cos 2 2 cos 2 cos cos 2cos + − + = 由: 得: 驻波方程
驻波方程 y=(2Acos2r )cos 2ru 分析: 1)驻波波形 t时刻波形: y==(2Acos2元4,)cos2r t,时刻波形: x y=,= (2Acos2πt2)cos2π 0≤A腹≤2A
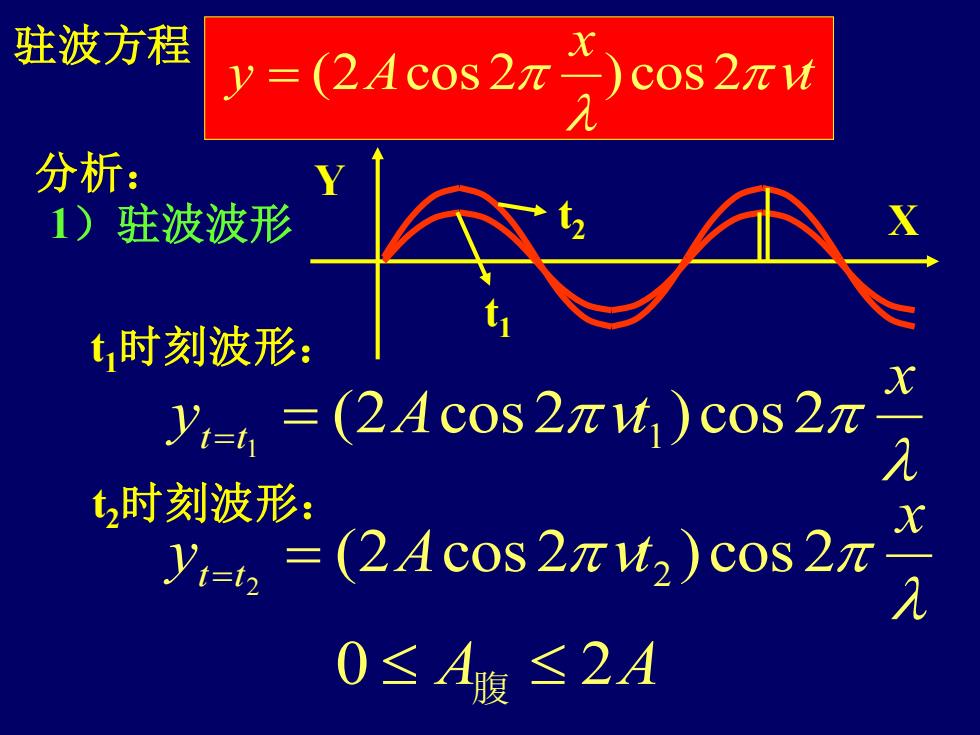
X Y t x y A = ( 2 cos 2 ) cos 2 驻波方程 分析: 1)驻波波形 x y A t t t ( 2 cos 2 1 ) cos 2 1 = = x y A t t t ( 2 cos 2 2 ) cos 2 2 = = t 1时刻波形: t 2时刻波形: t 1 t 2 0 A腹 2 A