
驻波方程 y=(2Acos2x )cos2u 分析: 2质点振动方程 X处质点B振动方程: =(24cos2z)cos2w X,处质点C振动方程: ()co2 各处质点振幅不同:0≤A质点≤2A
t x y A = (2 cos 2 ) cos 2 驻波方程 分析: 2质点振动方程 t x yx x A (2 cos 2 ) cos 2 1 1 = = X1处质点B振动方程: X2处质点C振动 方程: 0 A质点 2A t x yx x A (2 cos 2 ) cos 2 2 2 = = 各处质点振幅不同:
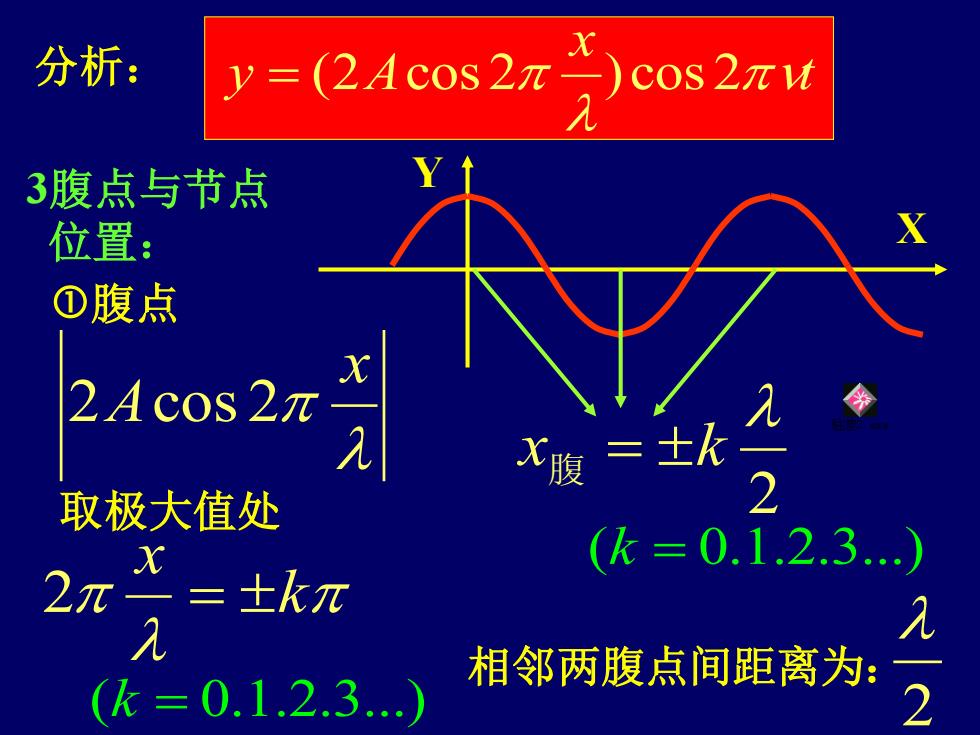
分析: X y=(24cos2x 3腹点与节点 位置: ①腹点 X 2Ac0S2元 X腹=士人 取极大值处 2 X (k=0.1.2.3. 2π 士k元 见 (k=0.1.2.3. 相邻两腹点间距离为: 2
t x y A 分析: = (2 cos 2 ) cos 2 3腹点与节点 位置: 腹点 k x 2 = (k = 0.1.2.3.) 2 x 腹 = k (k = 0.1.2.3.) x 2Acos 2 取极大值处 X Y 相邻两腹点间距离为: 2
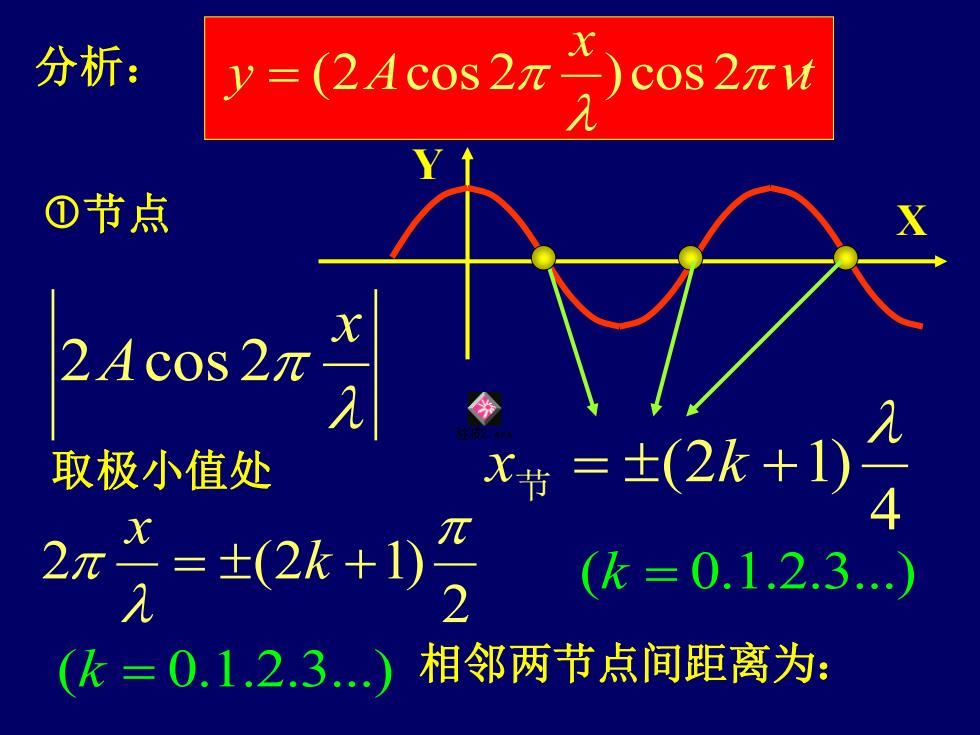
分析: y=(2Acos2π 月)cos2xw ①节点 2,4cos2元 取极小值处 x节=±(2k+1) 4 2n X=士(2k+1) (k=0.1.2.3. 2 (k=0.1.2.3.)相邻两节点间距离为:
t x y A 分析: = (2 cos 2 ) cos 2 X Y 节点 2 2 (2 1) = k + x (k = 0.1.2.3.) 4 (2 1) x 节 = k + (k = 0.1.2.3.) x 2Acos 2 取极小值处 相邻两节点间距离为: