《医学物理学》课程教学资源（PPT课件）电通量、电场中的高斯定理

置高斯定滋

93电通量电场中的高斯定理 一。 电力线（电场的图示法） 方向：切线 性质： 不闭合 大小：E= AN 电力线密度 不相交； AS 起于正、止于负

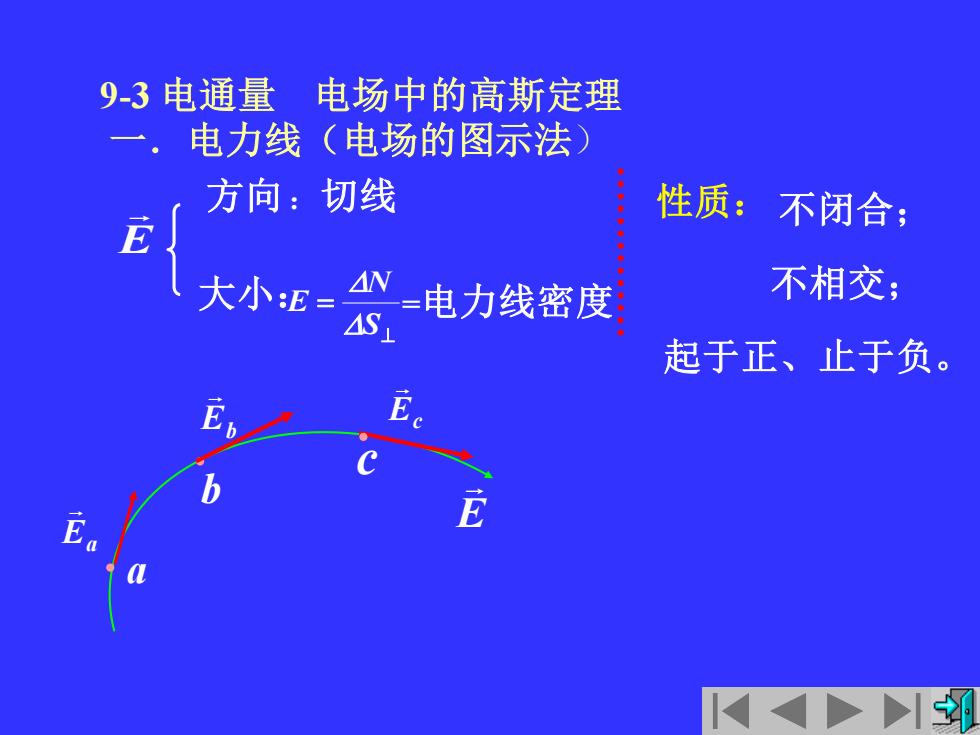
E  Ec  9-3 电通量 电场中的高斯定理 一．电力线（电场的图示法） ⊥ = S N E  大小：  E  方向：切线 =电力线密度 性质： b c Ea  Eb  a 不相交； 不闭合； 起于正、止于负

二.电通量Φ，（电场强度通量通过任一面的电力线数 Φ，=ES Φ=E●S=ESc0s0 E DE=∫E●瓜=∫Eds cos0 Φ。=fE●瓜=∮Ecos 0

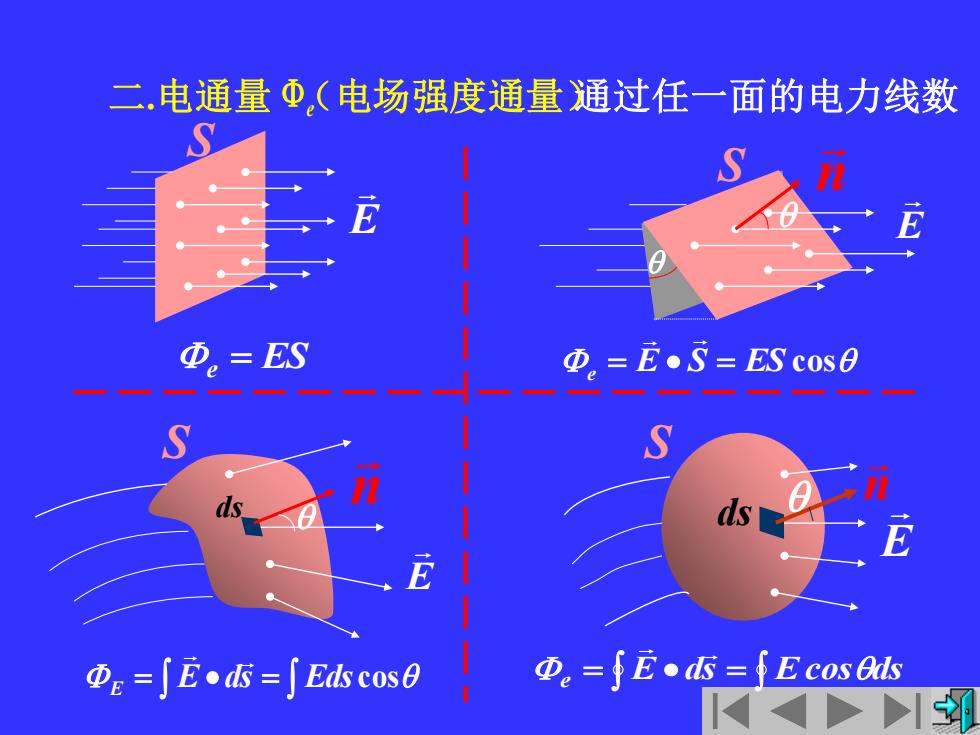
S E   S 二.电通量  （电场强度通量） e 通过任一面的电力线数 e = ES  E =  E • ds =  Eds cos   e = E • S = ES cos   =  E • ds =  Ecos ds e    S E  n   E  n  ds  S E ds  n  

例5.计算均匀电场中一圆柱面的电通量。己知E及R 解：。=手E本=∫E●+∫E本+∫E。 S1 S2 33 =∫Ecos180°+∫Ecos90°k+∫Ecos0°k S1 =-E元R2+0+元R2E =0 S2 R

S1 ds n  解： 例5．计算均匀电场中一圆柱面的电通量。已知 E  及 R =  • =  • +  • +  • 1 2 3 s s s e E ds E ds E ds E ds          =  +  +  1 2 3 0 0 0 180 90 0 s s s E cos E cos ds E cos ds E R R E 2 2 = −  + 0+ = 0 E  R S3 ds n  n  S2

1.求均匀电场中一半球面的电通量。 课堂练习 2.在均匀电场E=3i+2j中，过Y0Z平面内 面积为S的电通量。 X Φ=E。S Ds,+Ds2 =0 =(3i+2j)●Si Ds,+(-EπR2)=0 =3S Ds,=E元R2

1. 求均匀电场中一半球面的电通量。 2. 在均匀电场 E i j    = 3 + 2 中，过YOZ平面内 面积为S的电通量。 课 堂 练 习 E  R O n  n  n  n  S1 S2 0 1 2  S + S = 0 2 1  S + ( −ER ) = 2 1  S = ER E S    = • ( i j ) Si    = 3 + 2 • = 3S X O Y Z S E n  