
中国科学技术大学物理系微电子专业 内建电势的另一种求法: Jn=qDn dn +gnilE=O kT dlnn E 三 D I dn Ln n dx 9 dx Inn P 9 kT NAND bi Principle of Semiconductor Devices 2023/4/18 Tuesday 11
中国科学技术大学物理系微电子专业 11 Principle of Semiconductor Devices qn E 0 dx dn J n qDn n dx d n q kT dx dn n D E n n 1 ln N P n q kT V Edx P N bi ln 2 ln i A D bi n N N q kT V 内建电势的另一种求法: 2023/4/18 Tuesday

中国科学技术大学物理系微电子专业 §2.2 PN结的耗尽近似理论 耗尽近似理论,又称耗尽近似条件 在PN结的理论分析中,为简化问题的处理,常常 假设空间电荷区中正负电荷密度完全由电离杂质 浓度決定,从而忽略自由载流子的影响。 耗尽区 从中性区向结移动时,将遇到一个狭窄的过渡区 此处的杂质离子部分地被可动载流子补偿,经过 过渡区就是完全耗尽区,其中可动的载流子浓度 为零,这个区称为耗尽区,也叫空间电荷区。 一般地,对Si,GaAs的PN结,过渡区的宽度远小 于耗尽区,可以忽略过渡区。 Principle of Semiconductor Devices 2023/4/18 Tuesday 12
中国科学技术大学物理系微电子专业 12 Principle of Semiconductor Devices • 耗尽近似理论,又称耗尽近似条件 在PN结的理论分析中,为简化问题的处理,常常 假设空间电荷区中正负电荷密度完全由电离杂质 浓度决定,从而忽略自由载流子的影响。 • 耗尽区 从中性区向结移动时,将遇到一个狭窄的过渡区, 此处的杂质离子部分地被可动载流子补偿,经过 过渡区就是完全耗尽区,其中可动的载流子浓度 为零,这个区称为耗尽区,也叫空间电荷区。 • 一般地,对Si,GaAs的PN结,过渡区的宽度远小 于耗尽区,可以忽略过渡区。 §2.2 PN结的耗尽近似理论 2023/4/18 Tuesday
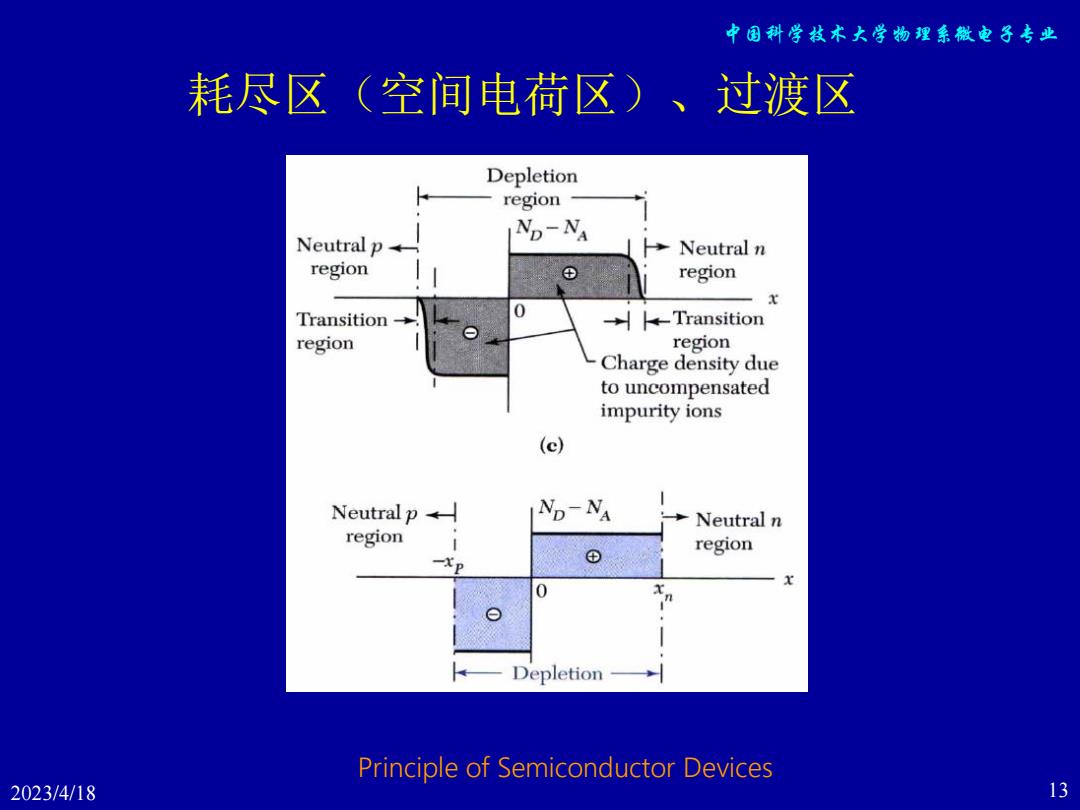
中国科学技术大学物理系微电子专业 耗尽区(空间电荷区)、过渡区 Depletion region Neutral p← ND-NA Neutral n region D region x Transition 0 →-Transition region region Charge density due to uncompensated impurity ions (c) Neutral p←l ND-NA Neutral n region region 一Xp ① 0 Depletion Principle of Semiconductor Devices 2023/4/18 13
中国科学技术大学物理系微电子专业 2023/4/18 Tuesday 13 Principle of Semiconductor Devices 耗尽区(空间电荷区)、过渡区

中国科学技木大学物理系微电子专业 1、热平衡时的耗尽区(耗尽层)特性 求解泊松方程,必须知道杂质分布。 PN结大致可以分为两种: (1)突变结:PN结两区中的杂质浓度为均匀分 布,且在交界面处发生杂质突变。如果一区的 杂质浓度远高于另一区,称为单边突变结PN 或NP结。由合金、浅扩散或低能离子注入形 成。 (2)线性缓变结:结附近, 其杂质分布是缓变 分布的,可以用直线近似,其斜率称为杂质浓 度梯度。由深扩散或高能离子注入制得的结。 Principle of Semiconductor Devices 2023/4/18 14
中国科学技术大学物理系微电子专业 2023/4/18 Tuesday 14 Principle of Semiconductor Devices 1、热平衡时的耗尽区(耗尽层)特性 • 求解泊松方程,必须知道杂质分布。 • PN结大致可以分为两种: (1)突变结:PN结两区中的杂质浓度为均匀分 布,且在交界面处发生杂质突变。如果一区的 杂质浓度远高于另一区,称为单边突变结 P +N 或 N+P结。由合金、浅扩散或低能离子注入形 成。 (2)线性缓变结:结附近,其杂质分布是缓变 分布的,可以用直线近似,其斜率称为杂质浓 度梯度。由深扩散或高能离子注入制得的结

中国科学技术大学物埋系微电子专业 (1)突变结 ·空间电荷区宽度向低掺杂浓度一侧展宽 Np'xn=NA'Xp 。泊松方程 d'y(x)p(x) dx2 Principle of Semiconductor Devices 2023/4/18 15
中国科学技术大学物理系微电子专业 2023/4/18 Tuesday 15 Principle of Semiconductor Devices (1)突变结 • 空间电荷区宽度向低掺杂浓度一侧展宽 • 泊松方程 D n A p N x N x s x dx d x ( ) ( ) 2 2