
(2)化学反应的反应速率 1d5 >化学反应速率r定义:r= y dt ·单位反应体积内反应进度随时间的变化率 >对一般反应cC+dDgG+hH 或0=∑B ·若反应系统体积V恒定: drsdi=dnc=dno =dredo dnB =d[B] VB g h V .r=1d[B]=_1dIC]=_1d[D]_1dlG]_1dlHJ VB dt c dt d dt g dt h dt ·用反应进度来定义,一个反应只有同一个速率值 ·无需指明所选用的物质,但需明确反应计量方程系数
(2) 化学反应的反应速率 化学反应速率r定义: • 单位反应体积内反应进度随时间的变化率 对一般反应 cC + dD gG + hH 或 0 = BB • 若反应系统体积V恒定: • 用反应进度来定义,一个反应只有同一个速率值 • 无需指明所选用的物质,但需明确反应计量方程系数 V t r d 1 d d[B] d d d d d d d C D G H B B B V n h n g n d n c n n 且 t c t d t g t h t r d 1 d[H] d 1 d[G] d 1 d[D] d 1 d[C] d 1 d[B] B

> 例如:反应2N2O,(g)→4NO2(g)+O2(g)中N2Os的瞬 时分解速率为4.2×10-7 mol dm-3.s1,求NO2和O2的 生成速率? 解:-1dN,0]_1dNo」_do] 2 dt 4 dt dt dN02l_-2dN,0l=2×4.2x10'=8.4×10'moldm3s dt dt d[o2]_1dN,O]_1 -×4.2×10-7=2.1×107 mol-dm3.s1 dt 2 dt 2 该化学反应速率: 1d[N,]1 d[NO:]d[o:1=2.1x107 mol'dm s- 2 dt 4 dt dt
例如:反应 2N2O5(g) 4NO2(g) + O2(g) 中N2O5的瞬 时分解速率为 4.2107 mol dm3·s1,求 NO2 和 O2 的 生成速率? • 解: 该化学反应速率: r =
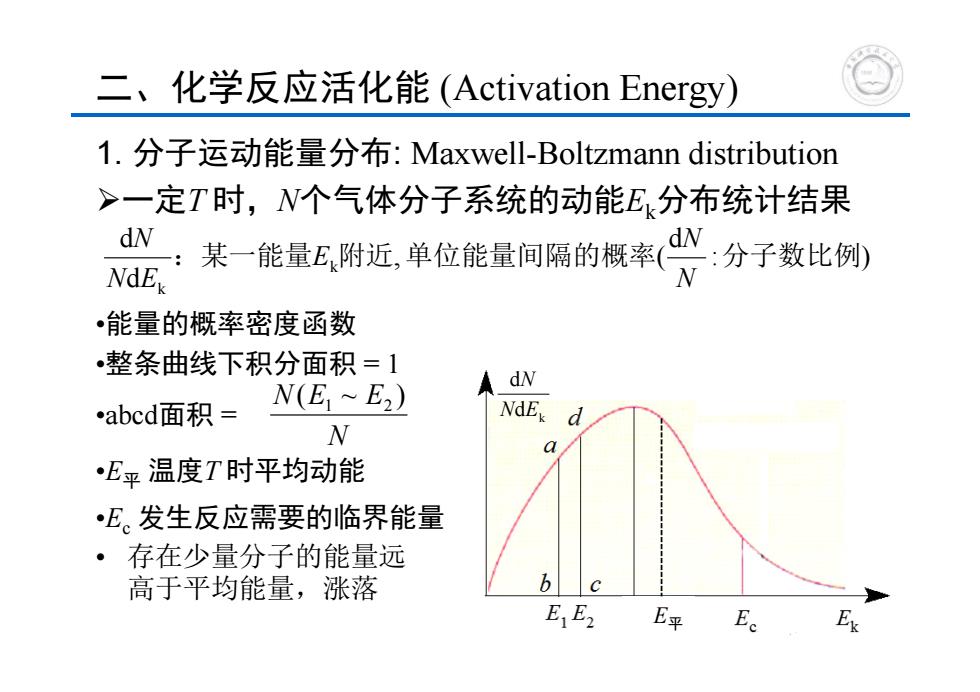
二、化学反应活化能(Activation Energy) 1.分子运动能量分布:Maxwell-Boltzmann distribution >一定T时,N个气体分子系统的动能E分布统计结果 能量E附近,单位能量何隔的概率· NdE •能量的概率密度函数 •整条曲线下积分面积=1 dN abcd面积= N(E1~E2) NdEx d N a •E平温度T时平均动能 •E。发生反应需要的临界能量 ·存在少量分子的能量远 高于平均能量,涨落 b☐c E E2 E平 E
1. 分子运动能量分布: Maxwell-Boltzmann distribution 一定T 时,N个气体分子系统的动能Ek分布统计结果 •能量的概率密度函数 •整条曲线下积分面积 = 1 •abcd面积 = •E平 温度T 时平均动能 •Ec 发生反应需要的临界能量 二、化学反应活化能 (Activation Energy) k d d N E N : ) d , ( dd k k :某一能量 附近 单位能量间隔的概率 分子数比例 NN E N EN N N(E ~ E ) 1 2 • 存在少量分子的能量远 高于平均能量,涨落 E平
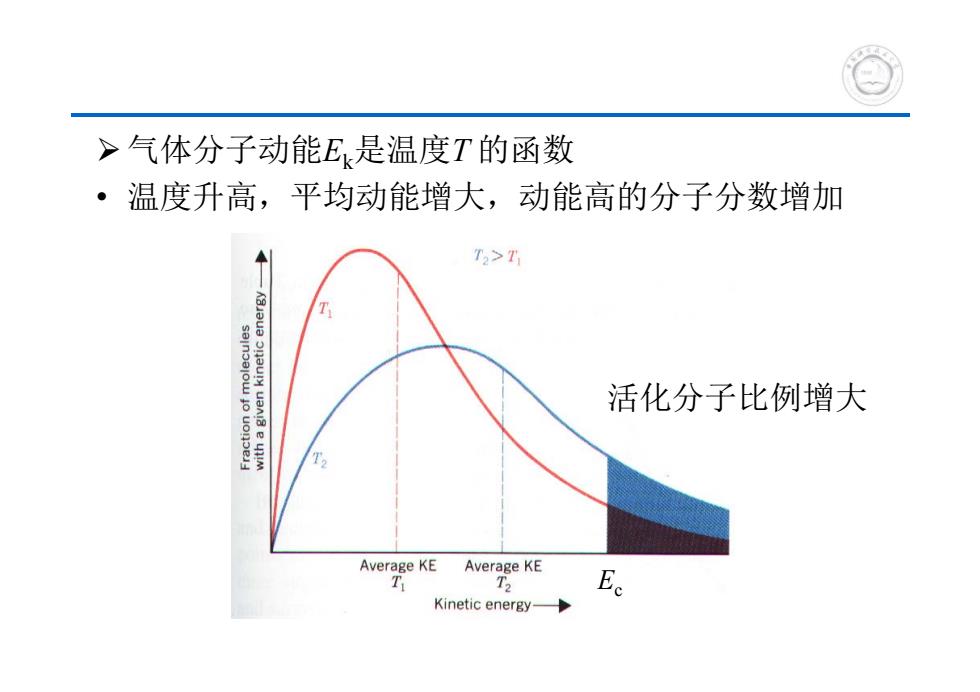
>气体分子动能E是温度T的函数 温度升高,平均动能增大,动能高的分子分数增加 T>T 活化分子比例增大 Average KE Average KE T Ee Kinetic energy-
气体分子动能Ek是温度T 的函数 • 温度升高,平均动能增大,动能高的分子分数增加 Ec 活化分子比例增大
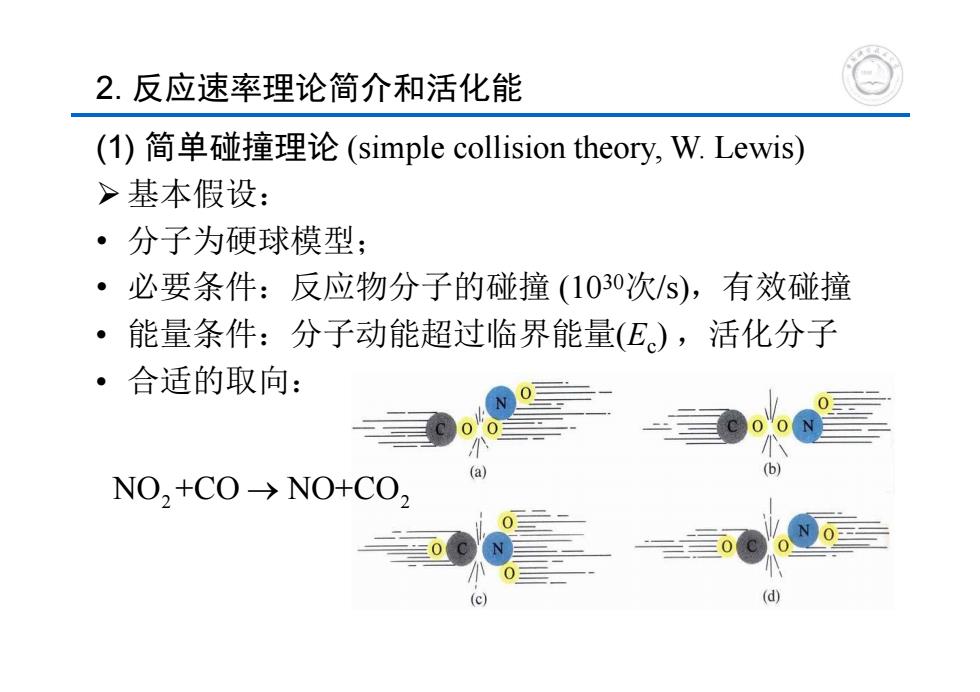
2.反应速率理论简介和活化能 (1)简单碰撞理论(simple collision theory,W.Lewis) >基本假设: ·分子为硬球模型; ·必要条件:反应物分子的碰撞(1030次/S),有效碰撞 能量条件:分子动能超过临界能量(E),活化分子 。 合适的取向: (a) b NO,+CO->NO+CO
2. 反应速率理论简介和活化能 (1) 简单碰撞理论 (simple collision theory, W. Lewis) 基本假设: • 分子为硬球模型; • 必要条件:反应物分子的碰撞 (1030次/s),有效碰撞 • 能量条件:分子动能超过临界能量(Ec) ,活化分子 • 合适的取向: NO +CO NO+CO 2 2