
版权©2019,版权保留,侵犯必究 第三章电阻电路的分析 电路的图 ·支路电流法和支路电压法 ●回路电流法 。节点电压法 复旦大学射频集成电路设计研究小组 -012- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -012- 第三章 电阻电路的分析 ⚫ 电路的图 ⚫ 支路电流法和支路电压法 ⚫ 回路电流法 ⚫ 节点电压法
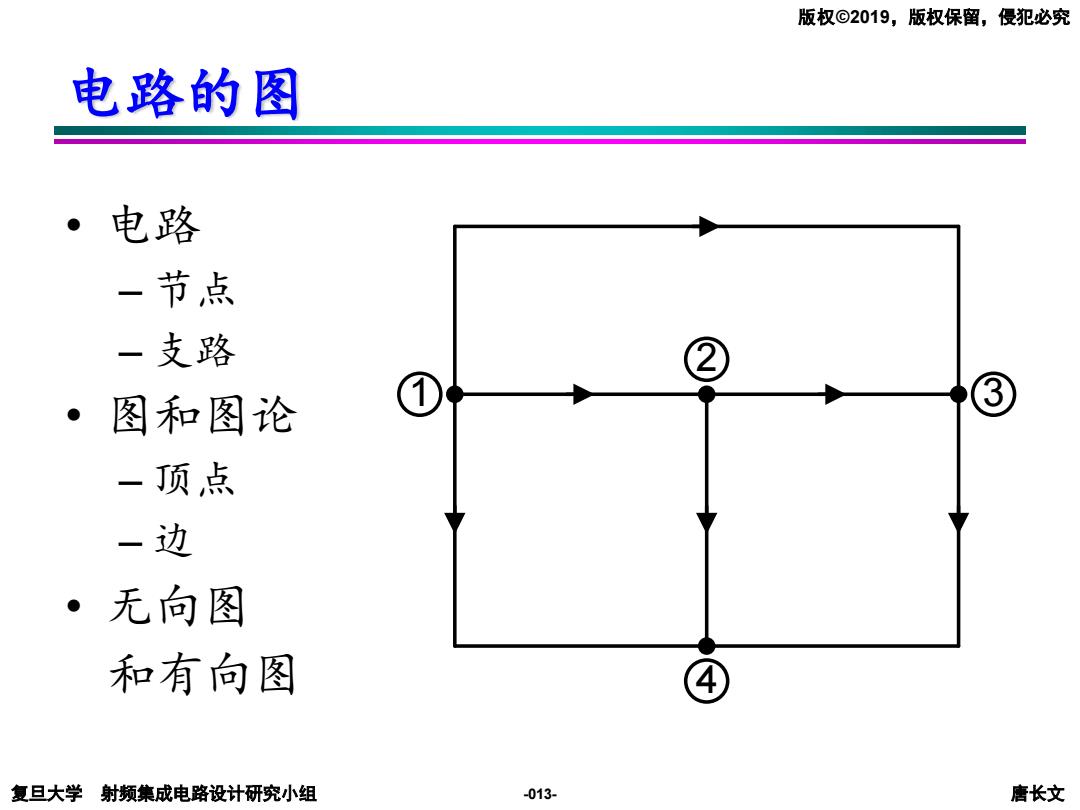
版权©2019,版权保留,侵犯必究 电路的图 。电路 一节点 一支路 ③ 图和图论 ③ 一顶点 一边 ·无向图 和有向图 ④ 复旦大学射频集成电路设计研究小组 -013- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -013- 6 4 5 1 2 3 1 2 3 4 电路的图 • 电路 – 节点 – 支路 • 图和图论 – 顶点 – 边 • 无向图 和有向图 6 4 5 1 2 3 1 2 3 4 6 4 5 1 2 3 1 2 3 4

版权©2019,版权保留,侵犯必究 路径,连通图和回路 ·路径 从一个顶点到另外一个顶点,经过的所有边构 成一条路径。 。连通图 任意两个顶,点之间至少有一条路径的图称为连 通图。 ·回路 如果一条路径的起点和终点重合,且经过的其 他顶,点不出现重复,这条闭合路径就是一个回路。 复旦大学射频集成电路设计研究小组 -014- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -014- 路径,连通图和回路 • 路径 从一个顶点到另外一个顶点,经过的所有边构 成一条路径。 • 连通图 任意两个顶点之间至少有一条路径的图称为连 通图。 • 回路 如果一条路径的起点和终点重合,且经过的其 他顶点不出现重复,这条闭合路径就是一个回路
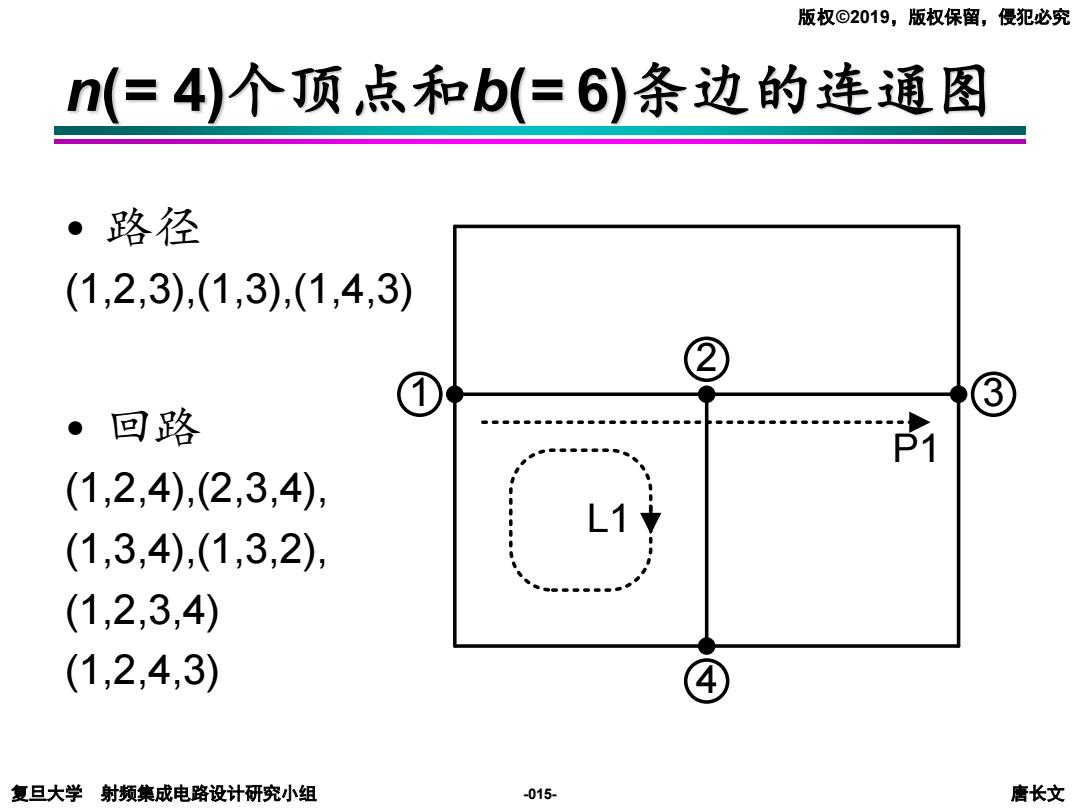
版权©2019,版权保留,侵犯必究 n(仁4)个顶点和b(=6)条边的连通图 ·路径 (1,2,3),(1,3),(1,4,3) ② ③ 回路 (1,2,4),(2,3,4); L1 (1,3,4),(1,3,2), (1,2,3,4) (1,2,4,3) ④ 复旦大学射频集成电路设计研究小组 -015- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -015- • 路径 (1,2,3),(1,3),(1,4,3) • 回路 (1,2,4),(2,3,4), (1,3,4),(1,3,2), (1,2,3,4) (1,2,4,3) n(= 4)个顶点和b(= 6)条边的连通图 6 4 5 1 2 3 1 2 3 4 L1 P1

版权©2019,版权保留,侵犯必究 树,树支和连支 ·树 包含图的全部顶点且不包含任何回路的连通子图。 ·树支 树中包含的边称为该树的树支。 ·连支 图中不包含在树中的边称为树的连支。 n个顶,点和b条边的连通图,其树的树支数为(n-), 连支数为(b-n+1)。 复旦大学射频集成电路设计研究小组 -016- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -016- 树,树支和连支 • 树 包含图的全部顶点且不包含任何回路的连通子图。 • 树支 树中包含的边称为该树的树支。 • 连支 图中不包含在树中的边称为树的连支。 n个顶点和b条边的连通图,其树的树支数为(n − 1), 连支数为(b − n + 1)