
常用组合逻辑电路种类很多,主要有全加器、 译码器、编码器、多路选择器、多路分配器、数 值比较器、奇偶检验电路等。 常用组合电路均有中规模集成电路(MS) 产品。 MS组合部件具有功能强、兼容性好、体积小、功 耗低、使用灵活等优点,因此得到广泛应用。本节主要 介绍几种典型MS组合逻辑部件的功能及应用
常用组合逻辑电路种类很多,主要有全加器、 译码器、编码器、多路选择器、多路分配器、数 值比较器、奇偶检验电路等。 常用组合电路均有中规模集成电路(MSI) 产品。 MSI组合部件具有功能强、兼容性好、体积小、功 耗低、使用灵活等优点,因此得到广泛应用。本节主要 介绍几种典型MSI组合逻辑部件的功能及应用

第三节 加法器 两个二进制数之间的算术运算无论是加、减、乘、 除,在计算机中都是化做若干步加法运算进行的。因此, 加法器是构成算术运算器的基本单元。 一、1位加法器 1、半加器 不考虑低位来的进位加法叫半加。 半加器:能完成半加功能的电路叫半加器
半加器:能完成半加功能的电路叫半加器。 不考虑低位来的进位加法叫半加。 两个二进制数之间的算术运算无论是加、减、乘、 除,在计算机中都是化做若干步加法运算进行的。因此, 加法器是构成算术运算器的基本单元
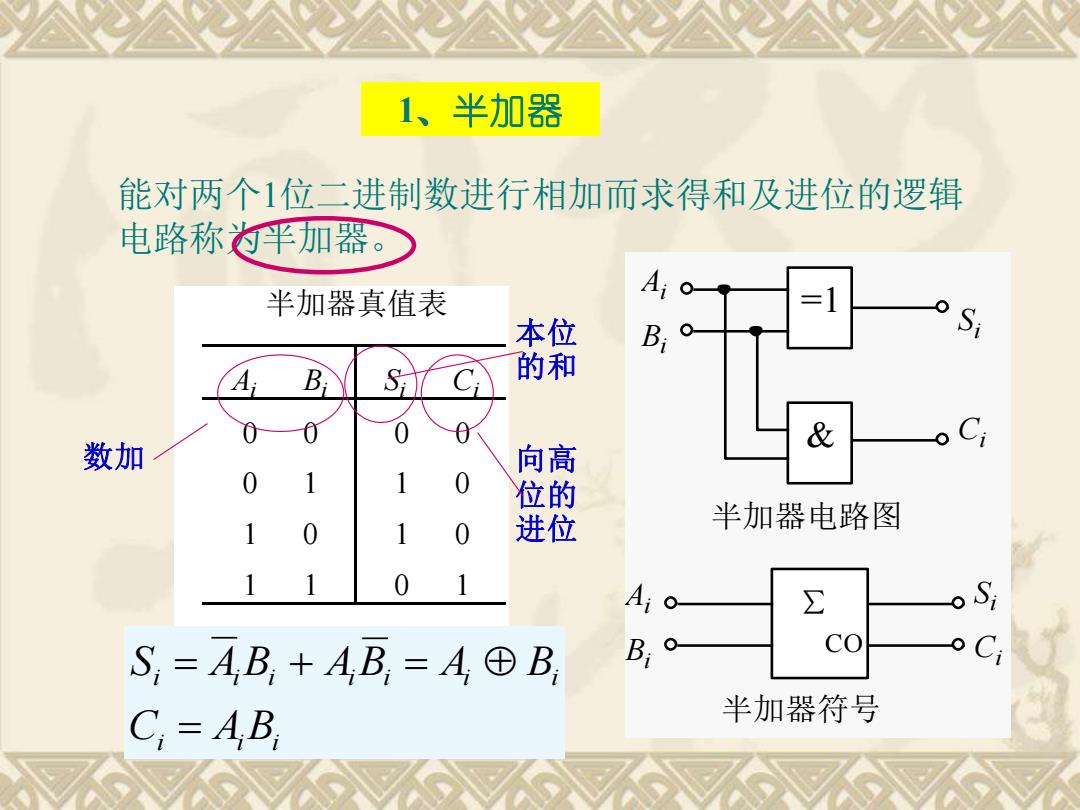
1、半加器 能对两个1位二进制数进行相加而求得和及进位的逻辑 电路称半加器。 半加器真值表 Ai 本位 Bi Si B 的和 数加 & 向高 位的 半加器电路图 1 进位 A10 ∑ S=AB+AB,=A©B B Q co C=AB 半加器符号
1、半加器 能对两个1位二进制数进行相加而求得和及进位的逻辑 电路称为半加器。 半加器真值表 Ai Bi Si Ci 0 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 i i i i i i i i i i C A B S A B A B A B = = + = =1 & Ai Bi Si Ci Ai Bi Si Ci ∑ CO 半加器符号 半加器电路图 数加 本位 的和 向高 位的 进位
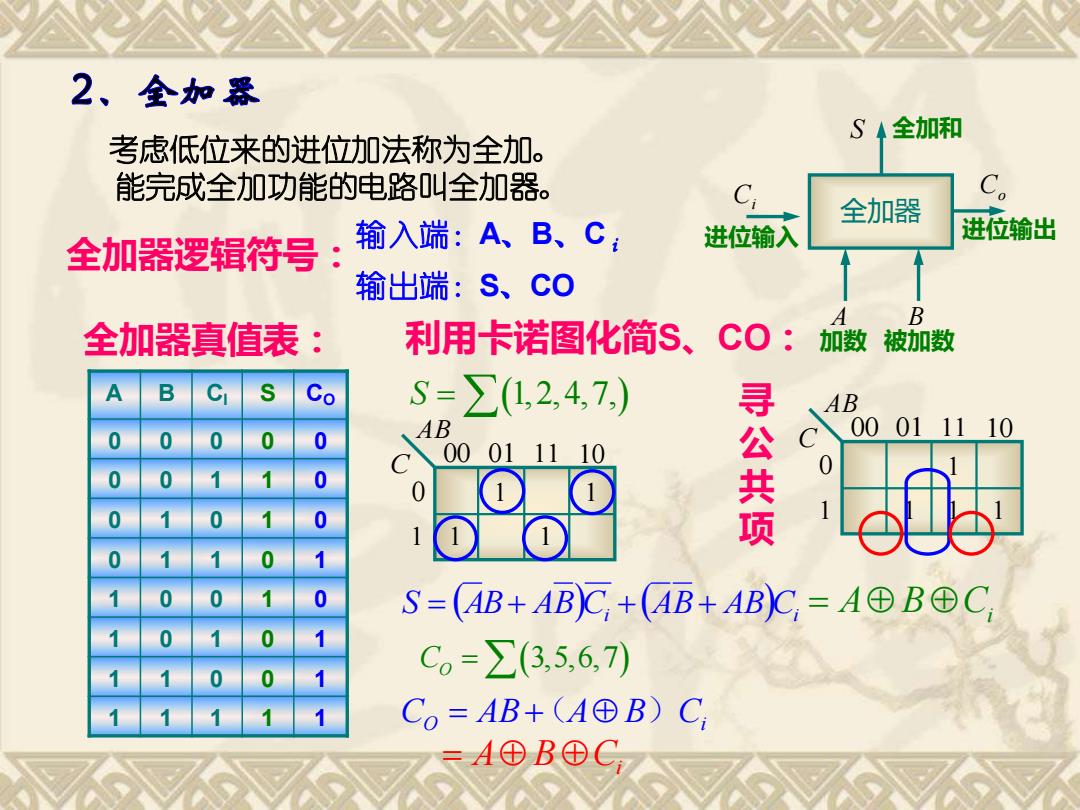
2、全加器 S◆全加和 考虑低位来的进位加法称为全加。 能完成全加功能的电路叫全加器。 C 全加器 全加器逻辑符号: 输入端:A、B、C: 进位输入 进位输出 输出端:S、CO B 全加器真值表: 利用卡诺图化简$、 CO:加数被加数 Co S=∑(1,2,4,7,) 寻 AB AB 00011110 00011110 0 公共项 S=(AB+AB)C,+AB+AB)C,=A田B⊕C Co=∑(3,5,6,7) CO=AB+(A⊕B)C =A⊕B⊕C
AB C 00 01 11 10 0 1 1 1 1 1 AB C 00 01 11 10 0 1 1 1 1 1 考虑低位来的进位加法称为全加。 能完成全加功能的电路叫全加器。 全加器逻辑符号:输入端:A、B、C i 输出端:S、CO 全加器真值表: A B CI S CO 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 利用卡诺图化简S、CO: S =(1,2,4,7,) ( ) ( ) S = AB+ AB Ci + AB+ AB Ci = A BCi CO =(3,5,6,7) CO = AB+(A B)Ci 寻 公 共 项 = A B Ci 进位输入 Ci 加数 A 全加和 全加器 进位输出 被加数 S Co B
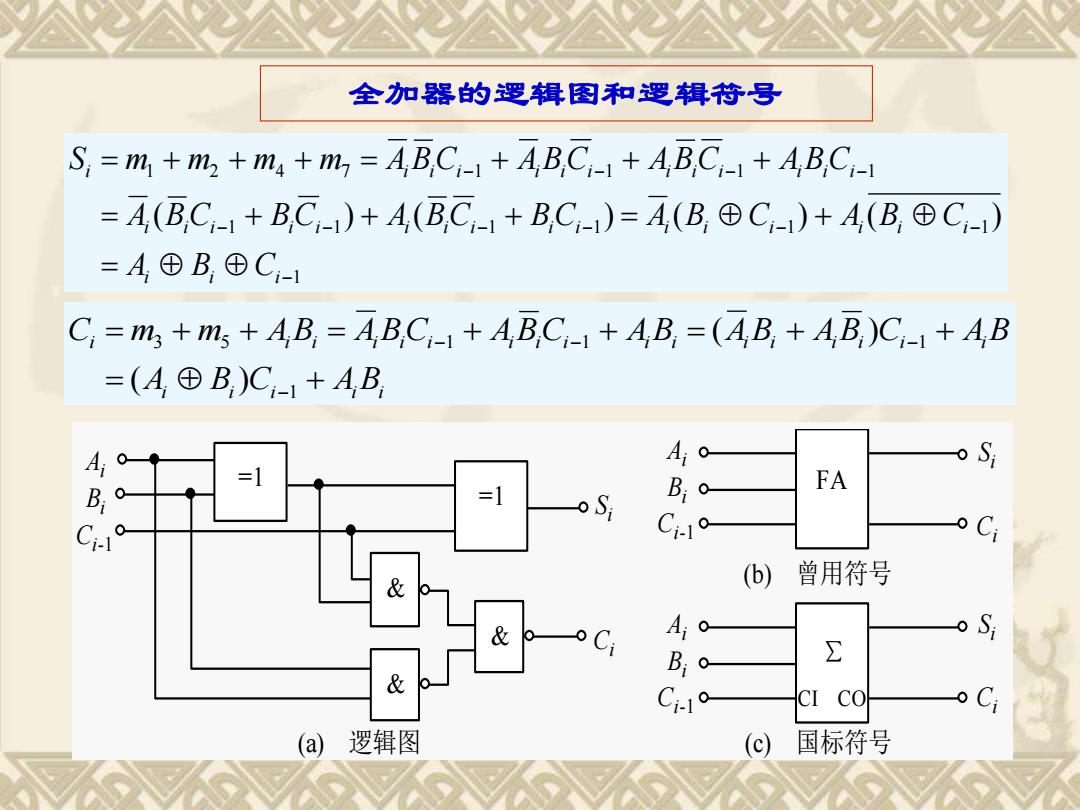
全加器的逻辑图和逻辑苻号 S,=m,+m2+m4+m,=AB.C-1+A,B,C-1+A,BC-1+AB,C,-1 =A(B,C-1+B,C-)+A,(BC-1+B,C-)=A,(B,⊕C-)+A(B,⊕C-) =A⊙B,©C-1 C,=m,+m+A,B,=A,B,C-1+A,B,C-1+A4B,=(4B,+AB,)C,-1+A,B =(A®B,)C-1+A,B Ai 0 S 4B =1 =1 FA C- 0 (b) 曾用符号 & o Ci A Q 0 B19 ∑ & Ci- CI CO a 逻辑图 (c) 国标符号
i i i i i i i i i i i i i i i i i i i i i i A B C AB C m m AB ABC ABC AB AB AB C AB = + = + + = + + = + + − − − − 1 3 5 1 1 1 ( ) ( ) 全加器的逻辑图和逻辑符号 = 1 & & Ai Bi Ci-1 Si Ci (a) 逻辑图 (c) 国标符号 Ai Bi Ci-1 Si Ci Ai Bi Ci-1 Si Ci (b) 曾用符号 CI CO ∑ & = 1 F A 1 1 1 1 1 1 1 1 2 4 7 1 1 1 1 ( ) ( ) ( ) ( ) − − − − − − − − − − − = = + + + = + = + + + = + + + i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i A B C A BC BC A BC BC A B C A B C S m m m m A BC A BC A BC A BC