
第六节逻辑函数的卡诺图化简法 2.6.1用卡诺图表示逻辑函数 利用卡诺图化简逻 必什么是卡诺图 辑函数,简捷直观 逻辑函数的卡诺图是一个特定 灵活方便且易于确 的方格图。每一个小方格代表 定是否已得到最简 了逻辑函数的最小项,且任意 结果。 两个相邻小方格所代表的最小 卡诺图是真值 项只有一个变量之差 表的一种特殊形式 ®卡洛图把逻辑函数中的逻辑相 是化简逻辑函数的 邻与几何相邻一一对应在方格 重要工具。 图
第六节 逻辑函数的卡诺图化简法 ❖ 什么是卡诺图 逻辑函数的卡诺图是一个特定 的方格图。每一个小方格代表 了逻辑函数的最小项,且任意 两个相邻小方格所代表的最小 项只有一个变量之差。 卡洛图把逻辑函数中的逻辑相 邻与几何相邻一一对应在方格 图。 利用卡诺图化简逻 辑函数,简捷直观, 灵活方便且易于确 定是否已得到最简 结果。 卡诺图是真值 表的一种特殊形式, 是化简逻辑函数的 重要工具。 2.6.1 用卡诺图表示逻辑函数
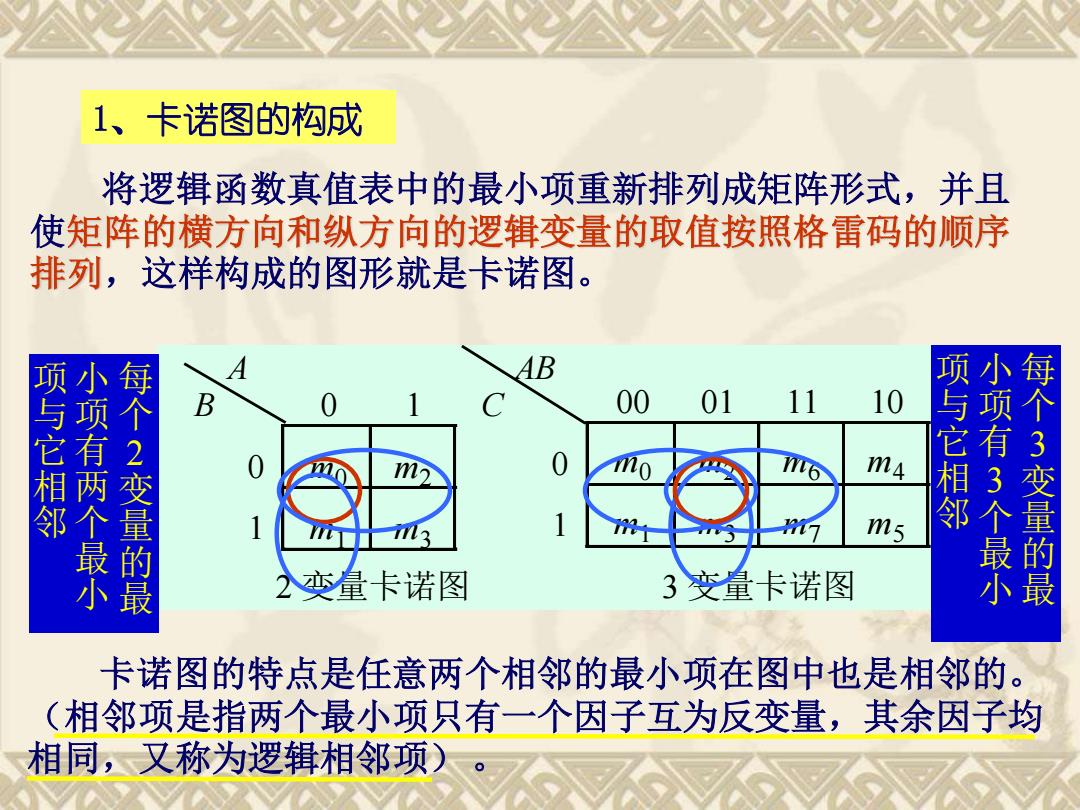
1、卡诺图的构成 将逻辑函数真值表中的最小项重新排列成矩阵形式,并且 使矩阵的横方向和纵方向的逻辑变量的取值按照格雷码的顺序 排列,这样构成的图形就是卡诺图。 项与它相邻 00 01 11 小项有两个最小 B 10 每个2变量的最 m 项与它相邻 m5 小项有3个最小 每个3变量的最 变量卡诺图 3交量卡诺图 卡诺图的特点是任意两个相邻的最小项在图中也是相邻的 。 (相邻项是指两个最小项只有一个因子互为反变量,其余因子均 相同,又称为逻辑相邻项)
1、卡诺图的构成 将逻辑函数真值表中的最小项重新排列成矩阵形式,并且 使矩阵的横方向和纵方向的逻辑变量的取值按照格雷码的顺序 排列,这样构成的图形就是卡诺图。 卡诺图的特点是任意两个相邻的最小项在图中也是相邻的。 (相邻项是指两个最小项只有一个因子互为反变量,其余因子均 相同,又称为逻辑相邻项)。 A B 0 1 0 m0 m2 1 m1 m3 AB C 00 01 11 10 0 m0 m2 m6 m4 1 m1 m3 m7 m5 2 变量卡诺图 3 变量卡诺图 每 个 2 变 量 的 最 小 项 有 两 个 最 小 项 与 它 相 邻 每 个 3 变 量 的 最 小 项 有 3 个 最 小 项 与 它 相 邻
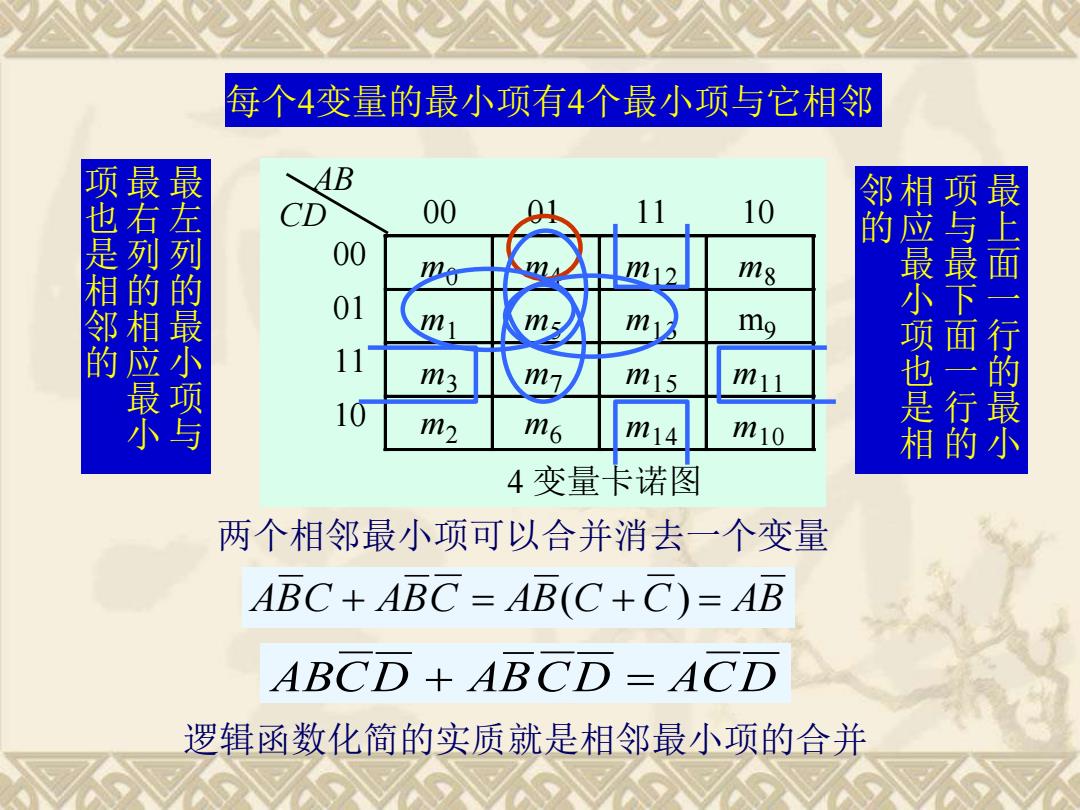
每个4变量的最小项有4个最小项与它相邻 B 项也是相邻的 00 10 最右列的相应最小 最左列的最小项与 00 m m8 01 mo 11 m3 m15 m11 袭 的 项与最下面一行的 最上面一行的最小 10 m2 m6 m14 m10 4变量卡诺图 两个相邻最小项可以合并消去一个变量 ABC+ABC =AB(C+C)=AB ABCD+ABCD-ACD 逻辑函数化简的实质就是相邻最小项的合并
AB CD 00 01 11 10 00 m0 m4 m1 2 m8 01 m1 m5 m1 3 m9 11 m3 m7 m1 5 m11 10 m2 m6 m1 4 m10 4 变量卡诺图 每个4变量的最小项有4个最小项与它相邻 最 左 列 的 最 小 项 与 最 右 列 的 相 应 最 小 项 也 是 相 邻 的 最 上 面 一 行 的 最 小 项 与 最 下 面 一 行 的 相 应 最 小 项 也 是 相 邻 的 两个相邻最小项可以合并消去一个变量 ABC + ABC = AB(C + C) = AB ABCD + ABCD = ACD 逻辑函数化简的实质就是相邻最小项的合并

2、卡诺图构图思想: (1)n变量函数就有2n个小方格。每个小方格相当于 真值表中的一个最小项。小方格的编号就是最小项的编号。 (2)每个相邻小方格彼此只允许一个变量不同。通常采 用格雷码排列。保证逻辑相邻,几何位置相邻。 (3) 卡诺图小方格相邻数=变量数
(3) 卡诺图小方格相邻数 = 变量数。 (2) 每个相邻小方格彼此只允许一个变量不同。通常采 用格雷码排列。保证逻辑相邻,几何位置相邻。 2、卡诺图构图思想: (1) n 变量函数就有 2 n 个小方格。每个小方格相当于 真值表中的一个最小项。小方格的编号就是最小项的编号
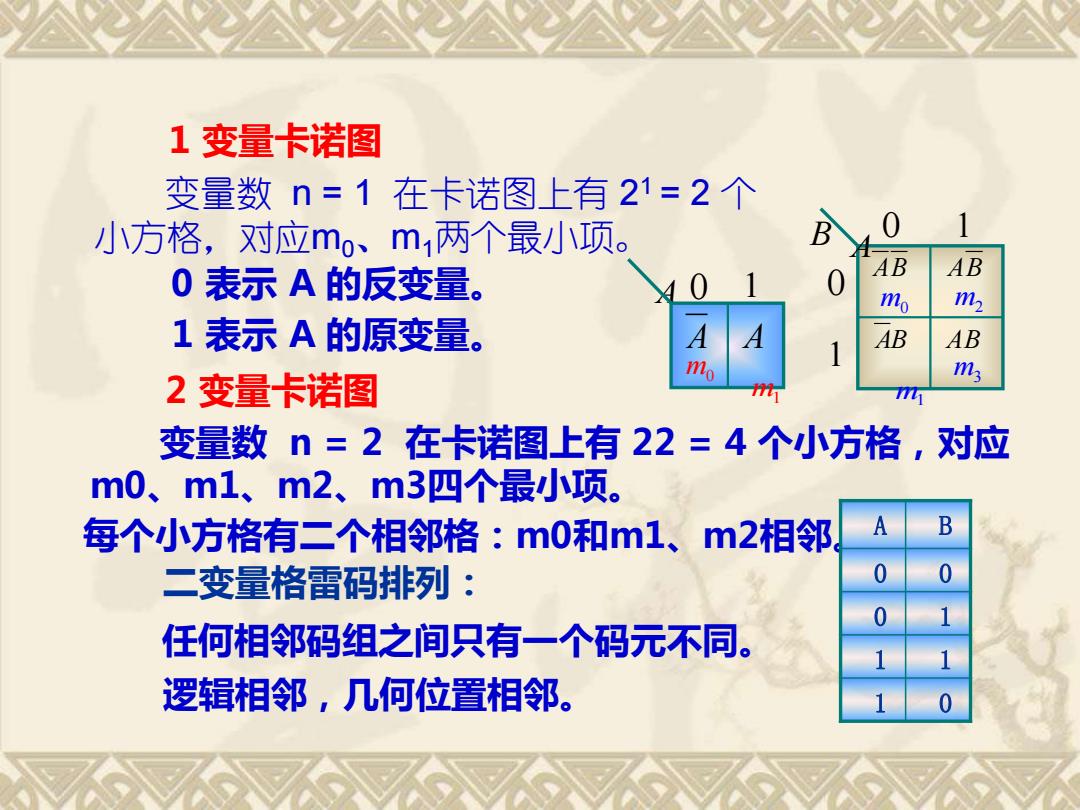
1变量卡诺图 变量数n=1在卡诺图上有21=2个 小方格,对应mo、m两个最小项。 1 0表示A的反变量。 AB AB mo m 1表示A的原变量。 A AB AB 2变量卡诺图 mo m, 变量数n=2在卡诺图上有22=4个小方格,对应 m0、m1、m2、m3四个最小项。 每个小方格有二个相邻格:m0和m1、m2相邻 B 二变量格雷码排列: 任何相邻码组之间只有一个码元不同。 逻辑相邻,几何位置相邻
1 变量卡诺图 变量数 n = 1 在卡诺图上有 2 1 = 2 个 小方格,对应m0、m1两个最小项。 0 表示 A 的反变量。 1 表示 A 的原变量。 2 变量卡诺图 变量数 n = 2 在卡诺图上有 22 = 4 个小方格,对应 m0、m1、m2、m3四个最小项。 每个小方格有二个相邻格:m0和m1、m2相邻。A B 0 0 0 1 1 1 1 0 二变量格雷码排列: 任何相邻码组之间只有一个码元不同。 逻辑相邻,几何位置相邻。 A B AB AB AB AB m1 m0 m2 m3 0 1 0 1 A 0 1 m0 m1 A A