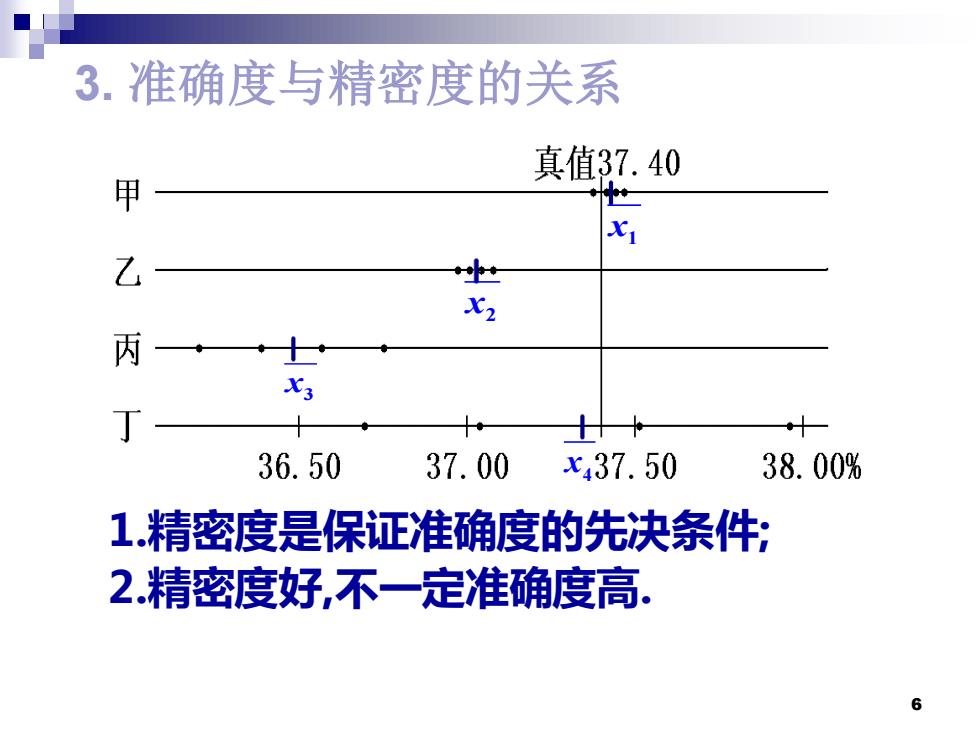
3.准确度与精密度的关系 真值37.40 甲 x1 乙 X2 丙 X3 丁 36.50 37.00 x437.50 38.00% 1.精密度是保证准确度的先决条件: 2.精密度好,不一定准确度高. 6
6 3. 准确度与精密度的关系 x1 x2 x3 x4 1.精密度是保证准确度的先决条件; 2.精密度好,不一定准确度高

2.1.2误差的产生及减免办法 1.系统误差 具单向性、重现性,为可测误差 方法:溶解损失、终点误差 一用其他方法校正 仪器:刻度不准、砝码磨损 一校准(绝对、相对) 操作:颜色观察 试剂:不纯一空白实验 对照实验:标准方法、标准样品、标准加入
7 2.1.2 误差的产生及减免办法 1. 系统误差 具单向性、重现性,为可测误差. 方法: 溶解损失、终点误差 — 用其他方法校正 仪器: 刻度不准、砝码磨损 — 校准(绝对、相对) 操作: 颜色观察 试剂: 不纯 — 空白实验 对照实验:标准方法、标准样品、标准加入

2.随机误差 (偶然误差) 不可避免,服从统计规律。 3.过失 由粗心大意引起,可以避免。 重徵/ 例:指示剂的选择 8
8 重 做 ! 例:指示剂的选择 2.随机误差 (偶然误差) 不可避免,服从统计规律。 3.过失 由粗心大意引起, 可以避免

2.2 随机误差的分布规律 2.2.1频率分布 事例: 测定w(BaCl22H2O):173个有效数据, 处于98.9%~100.2%范圃, 按0.1%组距分14组, 作频率密度测量值(6)图
9 2.2 随机误差的分布规律 2.2.1 频率分布 事例: 测定w(BaCl2·2H2O): 173个有效数据, 处于98.9% ~100.2%范围, 按0.1%组距分14组, 作 频率密度-测量值(%) 图
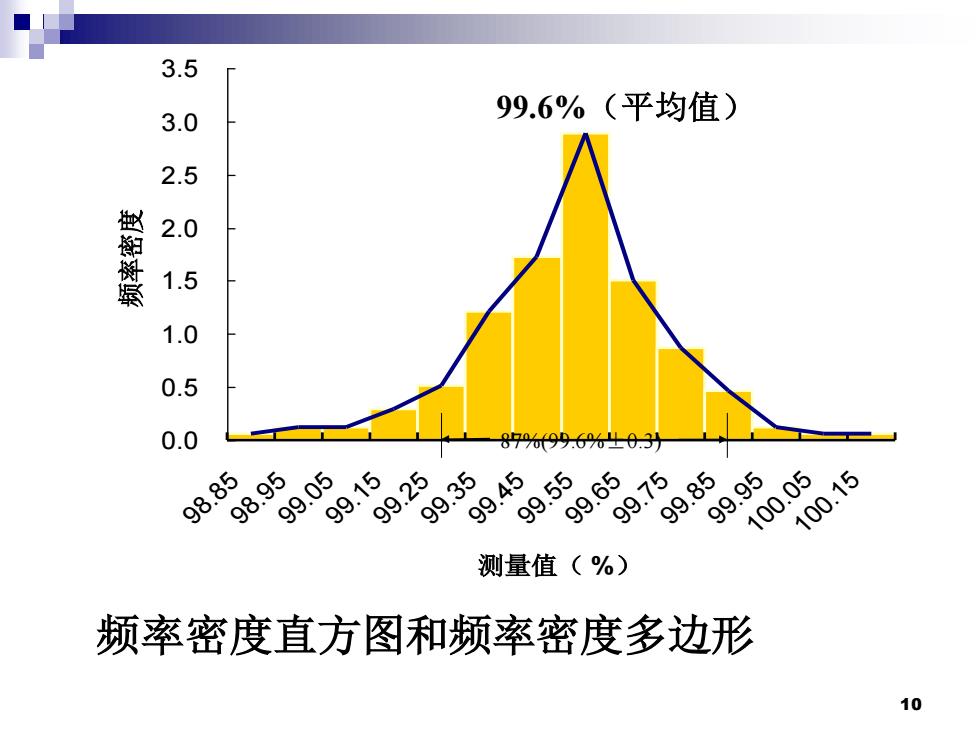
3.5 3.0 99.6%(平均值) 2.5 2.0 1.5 1.0 0.5 0.0 9%996%40.3引 98.85 9229329 99. 99 100.05 .9 100.15 测量值(%) 频率密度直方图和频率密度多边形 10
10 频率密度直方图和频率密度多边形 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 98.85 98.95 99.05 99.15 99.25 99.35 99.45 99.55 99.65 99.75 99.85 99.95 100.05 100.15 测量值( %) 频率密度 87%(99.6%±0.3) 99.6%(平均值)