
第十章核磁共振波谱分析 给源渭商業大是 HARBIN LNTVERSTTY OF COMMERCE
第十章 核磁共振波谱分析

第一节核磁共振原理 原子核的磁矩 原子核是带正电荷的粒子,和电子一样有自旋现象, 因而具有自旋角动量以及相应的自旋量子数。由于原子核 是具有一定质量的带正电的粒子,故在自旋时会产生核磁 矩。核磁矩和角动量都是矢量,它们的方向相互平行,且 磁矩与角动量成正比,即 uyp. (10.1) 式中:y为旋磁比(magnetogyricratio),rad T-1.sl, 即核磁矩与核的自旋角动量的比值,不同的核具有不同旋 磁比,它是磁核的一个特征值;为磁矩,用核磁子表示, 1核磁子单位等于5.05×10-27J·T1; 疮潮清月業大孕 HARBIN LNTVERSITY OF COMMERCE
第一节 核磁共振原理 一、原子核的磁矩 原子核是带正电荷的粒子,和电子一样有自旋现象, 因而具有自旋角动量以及相应的自旋量子数。由于原子核 是具有一定质量的带正电的粒子,故在自旋时会产生核磁 矩。核磁矩和角动量都是矢量,它们的方向相互平行,且 磁矩与角动量成正比,即 μ = γ p ( 10.1 ) 式中:γ为旋磁比(magnetogyricratio),rad·T−1·s−1 , 即核磁矩与核的自旋角动量的比值,不同的核具有不同旋 磁比,它是磁核的一个特征值;μ为磁矩,用核磁子表示, 1核磁子单位等于5.05×10−27J·T−1;

p为角动量,其值是量子化的,可用自旋量子数表 示为角动量,其值是量子化的,可用自旋量子数表 p= (10.2) 式中:h为普郎克常数(6.63×10-34Js);-为 自旋量子数,与原子的质量数及原子序数有关。式中: h为普郎克常数.(6.63×10-34Js);-为自旋量子数, 与原子的质量数及原子序数有关。 给源渭商業大是 HARBIN LNTVERSTTY OF COMMERCE
p为角动量,其值是量子化的,可用自旋量子数表 示p为角动量,其值是量子化的,可用自旋量子数表 ( 10.2 ) 式中:h为普郎克常数(6.63×10−34J·s);−I为 自旋量子数,与原子的质量数及原子序数有关。式中: h为普郎克常数(6.63×10−34J·s);−I为自旋量子数, 与原子的质量数及原子序数有关。 ( 1) 2 = I I + h p
自旋量子数与原子的质量数及原子序数的关系见表: 质量数A 原子序数Z 自旋量子数·INMR信号 ·原子核 偶数 偶数 无 12C6 160g32S16 奇数 奇或偶数 /2 有 1H1,13C6 19Fg 15N7, 31P5 奇数 奇或偶数 3/2,5/2. 有 108 33S16 偶数 奇数 1,2,3 有 2H1, 14N7 疮爾清月業大孕 HARBIN LNTVERSITY OF COMMERCE
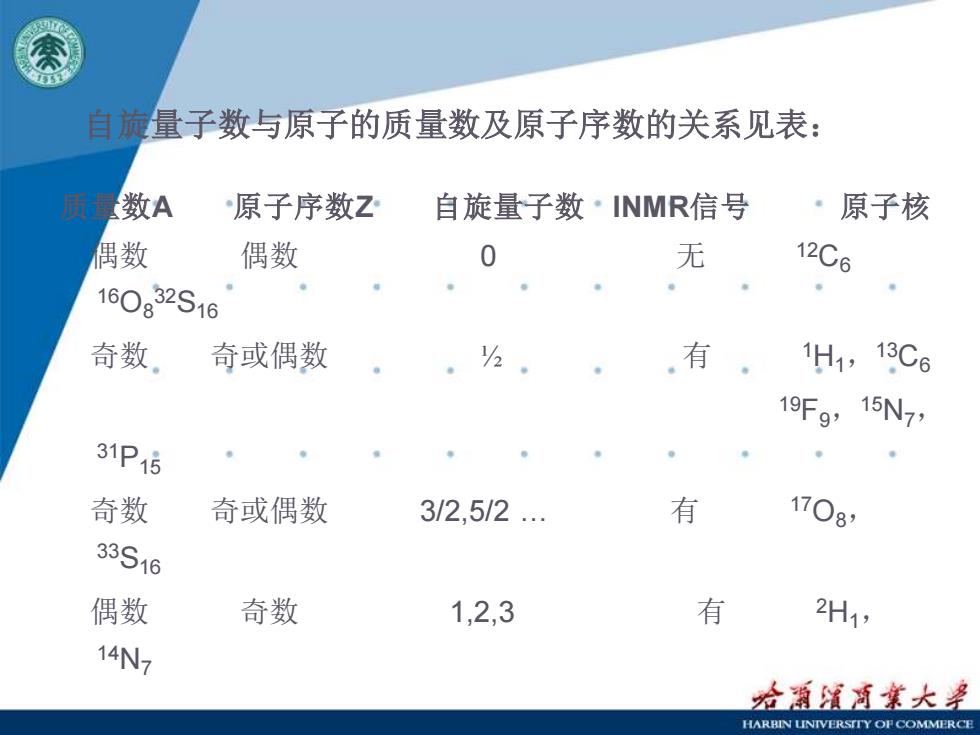
自旋量子数与原子的质量数及原子序数的关系见表: 质量数A 原子序数Z 自旋量子数 INMR信号 原子核 偶数 偶数 0 无 12C6 16O8 32S16 奇数 奇或偶数 ½ 有 1H1, 13C6 19F9, 15N7, 31P15 奇数 奇或偶数 3/2,5/2 . 有 17O8, 33S16 偶数 奇数 1,2,3 有 2H1, 14N7

当=0时,p=0,原子核没有磁矩,没有自旋现象;当/ 。】 >0时,p≠0,.原子核磁矩不为零,.有自旋现象。 =1/2的原子核在自旋过程中核外电子云呈均匀的球 。 型分布,见图10.1(b)核磁共振谱线较窄,最适宜核 磁共振检测,是NMR主要的研究对象。>1/2的原子 ,核,.自旋过程中申荷在核表面非均匀分布 1=0 1=1/2 /=1,3/2.2. (a) (b) (c) 图10.1原子核的自旋形状 宏酒演商常大是 HARBIN LNIVERSTTY OF COMMERCE
当I=0时,p=0,原子核没有磁矩,没有自旋现象;当I >0时,p≠ 0,原子核磁矩不为零,有自旋现象。 I=1/2的原子核在自旋过程中核外电子云呈均匀的球 型分布,见图10.1(b)核磁共振谱线较窄,最适宜核 磁共振检测,是NMR主要的研究对象。I>1/2的原子 核,自旋过程中电荷在核表面非均匀分布 图10.1 原子核的自旋形状