
(2) 设D的第i行除了外都是0。 j : D= 0 0 把D转化为(1)的情形 : 。 把D的第i行依次与第i-1行,第i-2行,., 第2行,第1行交换;再将第j列依次与第j-1列, 第j-2列,.,第2列,第1列交换,这样共经过 (i-1)+(j-1)=i+j-2次交换行与交换列的步骤。 6
6 (2) 设 D 的第 i 行除了 ij a 外都是 0 。 n nj nn ij j n a a a a a a a D 1 11 1 1 = 0 0 把D转化为(1)的情形 把 D 的第 i 行依次与第 i − 1 行,第 i − 2 行,······, 第2行,第1行交换;再将第 j 列依次与第 j − 1 列, 第 j − 2 列,······,第2列,第1列交换,这样共经过 (i − 1) + ( j − 1) = i + j − 2 次交换行与交换列的步骤

由性质2,行列式互换两行(列)行列式变号, 得, 0 0 : D=(-1)+i- Ai-1,j li-1, .: : 心d 0n,j-1 nn =(-1)+aM,=(-1)+A
7 由性质2,行列式互换两行(列)行列式变号, 得, nj n j nn i j i j i n i j i j a a a a a a a D , 1 1, 1, 1 1, 2 0 0 ( 1) − − − − − + − = − ij i j ij ij i j a M A + + = (−1) = (−1)
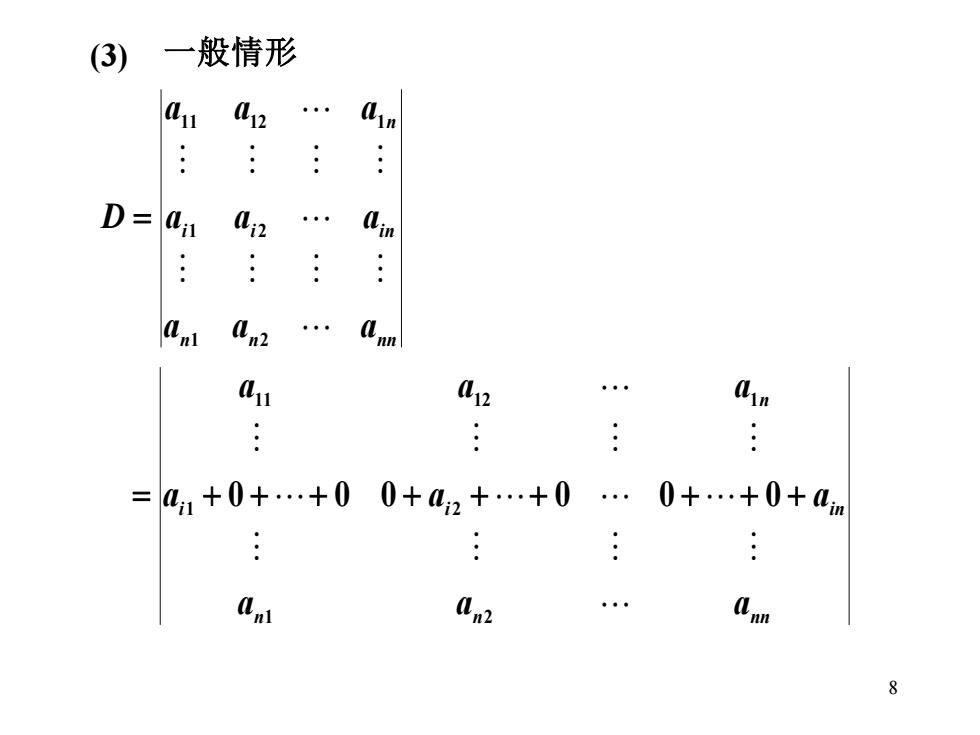
(3) 一般情形 12 n .: D= n n m . Am Am2 11 2 =41+0+.+00+42+.+0 0+.+0+4m : 2 n 8
8 (3) 一般情形 n n nn i i in n a a a a a a a a a D 1 2 1 2 11 12 1 = n n nn i i i n n a a a a a a a a a 1 2 1 2 11 12 1 = + 0 + + 0 0 + + + 0 0 + + 0 +

2 . n 2 : : : .: ·: 0 0 0 Ap 0 +.十 0 0 Ain : : . 4n2 =a1A1+a2A2+.+0nAm (i=1,2,.,n) 证毕。 -3-53 例如,行列式D= 0-1 0 按第一行展开,得 72 -10 722 0 D=-3 +5
9 n n nn i n a a a a a a a 1 2 1 11 12 1 = 0 0 n n nn i n a a a a a a a 1 2 2 11 12 1 + 0 0 n n nn in n a a a a a a a 1 2 11 12 1 + + 0 0 = ai1Ai1 + ai 2Ai 2 ++ ainAin (i = 1,2, ,n) 例如,行列式 7 7 2 0 1 0 3 5 3 − − − D = 7 2 1 0 3 − D = − 按第一行展开,得 7 2 0 0 + 5 7 7 0 1 3 − + 证毕

定理2: 行列式任一行(列)的元素与另一行(列)的对应 元素的代数余子式乘积之和等于零,即 k1A1+0k2A2+.+0An=0,k≠i. 证明: 由定理1,行列式等于某一行的元素分别与它们 代数余子式的乘积之和。 12 da (l2 Ain 在D= 中,如果令第i行的元素等于 Qki Ak2 kn 另外一行,譬如第k行的元素 0m2 Cnn 10
10 行列式任一行(列)的元素与另一行(列)的对应 元素的代数余子式乘积之和等于零,即 0, . 1 1 2 2 a A a A a A k i k i + k i ++ kn i n = 定理2: 证明: 由定理1,行列式等于某一行的元素分别与它们 代数余子式的乘积之和。 在 n n nn k k kn i i in n a a a a a a a a a a a a D 1 2 1 2 1 2 11 12 1 = 中,如果令第i 行的元素等于 另外一行,譬如第k 行的元素