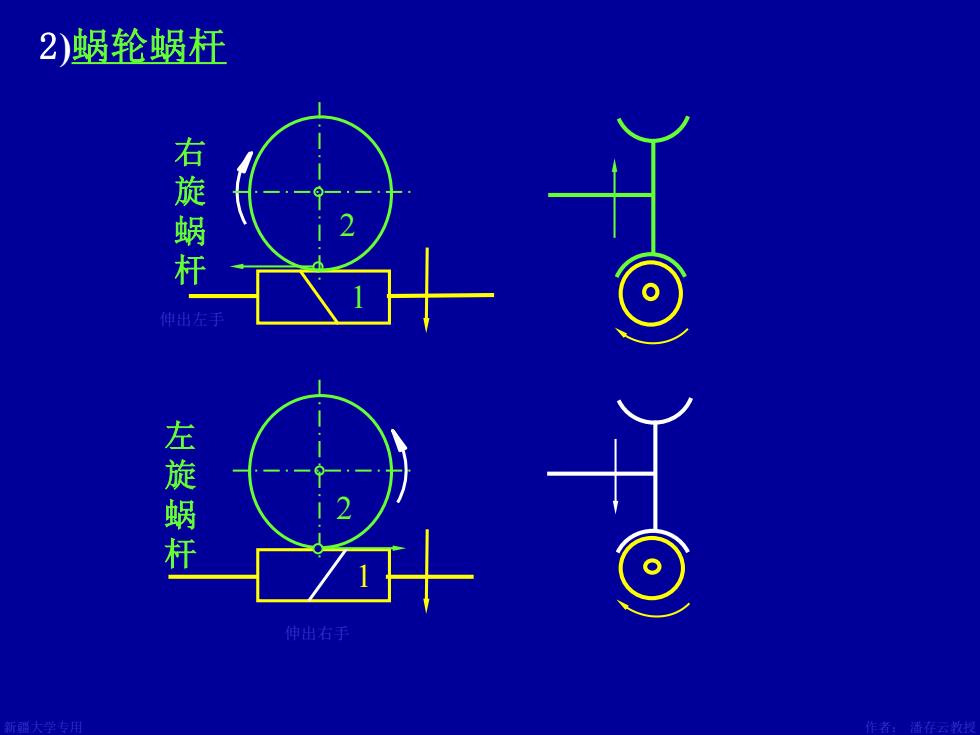
2)蜗轮蜗枉 右旋蜗杆 e 左旋蜗杆 伸出右手
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 左旋蜗杆 1 2 2 )蜗轮蜗杆 伸出左手 伸出右手 右旋蜗杆 21
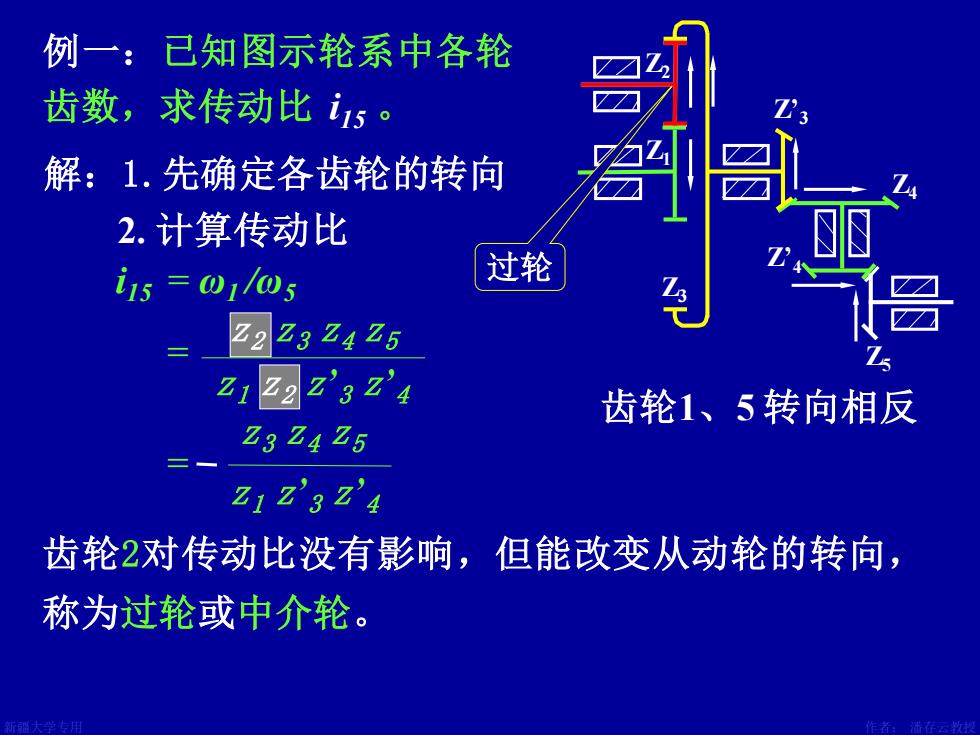
例一:已知图示轮系中各轮 齿数,求传动比i5。 解:1.先确定各齿轮的转向 2.计算传动比 i15=0105 过轮 22232425 21Z2z'3z'4 齿轮1、5转向相反 Z3Z425 Z1Z’3Z'4 齿轮2对传动比没有影响,但能改变从动轮的转向, 称为过轮或中介轮
新疆大学专用 作者: 潘存云教授 设计:潘存云 Z1 Z’3 Z4 Z’4 Z5 Z2 Z3 例一:已知图示轮系中各轮 齿数,求传动比 i15 。 齿轮2对传动比没有影响,但能改变从动轮的转向, 称为过轮或中介轮。 2. 计算传动比 齿轮1、5 转向相反 解:1.先确定各齿轮的转向 过轮 z1 z2 z’ 3 z’ 4 z2 z3 z4 z5 = z1 z’ 3 z’ 4 z3 z4 z5 = i15 = ω1 /ω5

§5一3周转轮系及其传动比 基本构件:太阳轮(中心轮)、行星架(系杆或转臂)。 其它构件:行星轮。 其运动有自转和绕中心轮前公转,类似行星运动,故得名 类型: 由于轮2既有自转又有公转敌不 2K-H型 3K型 能直按求传动比 H 3和系杆作 一®后系杆成为机烟 转化为定轴轮 反转原理:给周转轮系施以附加的公共转动一⊙后,不改变轮 系中各构件之间的相对运动,但原轮系将转化成为一新的定 轴轮系,可按定轴轮系的公式计算该新轮系的传动比。 转化后所得轮系称为原轮系的“转化轮系
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 设计:潘存云 2 H 2 H 1 3 1 3 反转原理:给周转轮系施以附加的公共转动-ωH后,不改变轮 系中各构件之间的相对运动, 但原轮系将转化成为一新的定 轴轮系,可按定轴轮系的公式计算该新轮系的传动比。 类型: 基本构件:太阳轮(中心轮)、行星架(系杆或转臂)。 其它构件:行星轮。其运动有自转和绕中心轮的公转,类似行星运动,故得名。 §5-3 周转轮系及其传动比 转化后所得轮系称为原轮系的 2K-H型 3K型 “转化轮系” -ωH ω1 ω3 ω2 施加-ωH后系杆成为机架,原轮系转化为定轴轮系 由于轮2既有自转又有公转,故不 能直接求传动比 轮1、3和系杆作定 轴转动 ωH

将轮系按一⊙反转后,各构件的角速度的变化如下: 构件 原角速度 转化后的角速度 1 D H 2 D 2 GωH 02一 3 ⊙3 H ⊙H H ⊙H @H 三0H一0H=0 ☑ 转化后:系杆=>机架,周转轮系=>定轴轮系, 可直接套用定轴轮系传动比的计算公式
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 1 ω1 将轮系按-ωH反转后,各构件的角速度的变化如下: 2 ω2 3 ω3 H ωH 转化后: 系杆=>机架, 周转轮系=>定轴轮系, 构件 原角速度 转化后的角速度 2 H 1 3 可直接套用定轴轮系传动比的计算公式。 ωH 1=ω1-ωH ωH 2=ω2-ωH ωH 3=ω3-ωH ωH H=ωH-ωH=0 2 H 1 3

01-0H 2223 03-0H 2122 21 上式“一” 说明在转化轮系中oH1与o。方向相反。 通用表达式: 右边各的齿数为己知, 个基本件的参中 如果已其中任意两个 则可求得第三个颈。 可求得任意两个构件之间的传动比 H m 0m-0H mn 0n-0H 转化轮系中由m至n各从动轮的乘积 转化轮系中由m至n各主动轮的乘积 f 特别注意: 1.齿轮m、n的轴线必须平行。 2.计算公式中的“±”不能去掉,它不仅表明转化 轮系中两个太阳轮m、n之间的转向关系,而且影响 到⊙m、On、⊙的计算结果
新疆大学专用 作者: 潘存云教授 右边各轮的齿数为已知,左边三个基本构件的参数中,如果已知其中任意两个, 则可求得第三个参数。于是,可求得任意两个构件之间的传动比。 上式“-”说明在转化轮系中ωH 1 与ωH 3 方向相反。 特别注意: 1.齿轮m、n的轴线必须平行。 H H H i 3 1 13 = 1 2 2 3 z z z z = − 1 3 z z = − 通用表达式: H n H H m mn i = n H m H − − = 转化轮系中由 至 各主动轮的乘积 转化轮系中由 至 各从动轮的乘积 m n m n = = f(z) H H − − = 3 1 2.计算公式中的“±” 不能去掉,它不仅表明转化 轮系中两个太阳轮m、n之间的转向关系,而且影响 到ωm、ωn、ωH的计算结果