3峰值吸收 ,=1dv;1=1ay 将Ieb代入上式:i=1edv 则:A=g dv 吸收线 a.d △a 采用锐线光源进行测量,则 △ △V。<△va,由图可见,在辐射线宽度 〈△V。 峰值吸收 范围内,飞可近似认为不变,并近 发射线 似等于峰值时的吸收系数K
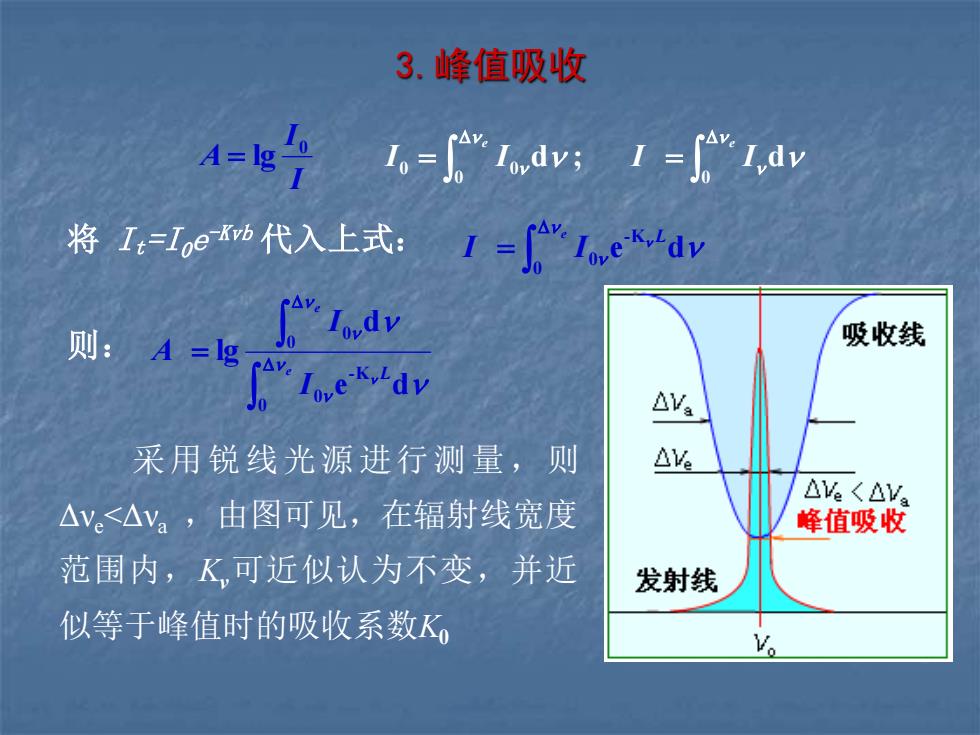
3.峰值吸收 采用锐线光源进行测量 ,则 Δνe<Δνa ,由图可见,在辐射线宽度 范围内,Kν可近似认为不变,并近 似等于峰值时的吸收系数K0 I I A 0 = lg = = e e I I I I 0 0 0 0 d ; d = e L I I 0 -K 将 It=I0e 0 e d -Kvb 代入上式: = e e L I I A 0 -K 0 0 0 e d d 则: lg

峰值吸收 A =lg A=g。=ge=0.434KL 在原子吸收中,谱线变宽主要受多普勒效应影响,则: Ko= 2vn In 2 e2 △yb mc A=0.4342元h2 NL=LN。 △yb mc 吸收线 上式的前提条件: △v △ (1)△v<△ya; △<AY2 蜂值吸收 发射线 (2)辐射线与吸收线的中心频率一致
峰值吸收 在原子吸收中,谱线变宽主要受多普勒效应影响,则: = e e L I I A 0 -K 0 0 0 e d d lg A K L K L -K L 434 0 lg e 0. e 1 lg 0 = = = N f mc e K 0 2 D 0 2 π ln 2 = 0 0 2 D 2 π ln 2 0.434 N fL kLN mc e A = = 上式的前提条件: (1) Δνe<Δνa ; (2)辐射线与吸收线的中心频率一致

五、基态原子数与原子化温度 原子吸收光谱是利用待测元素的原子蒸气中基态原子与 共振线吸收之间的关系来测定的。 需要考虑原子化过程中,原子蒸气中基态原子与待测元 素原子总数之间的定量关系。 热力学平衡时,两者符合Boltzmann分布定律: Nj_P, Eo-Ei -△E kT e kT e kT No Po P P 上式中P和P分别为激发态和基态的统计权重,激发态 原子数W与基态原子数6之比较小,<1%.可以用基态原子数 代表待测元素的原子总数。公式右边除温度T外,都是常数 T一定,比值一定
五、基态原子数与原子化温度 原子吸收光谱是利用待测元素的原子蒸气中基态原子与 共振线吸收之间的关系来测定的。 需要考虑原子化过程中,原子蒸气中基态原子与待测元 素原子总数之间的定量关系。 热力学平衡时,两者符合Boltzmann分布定律: 上式中Pj和PO分别为激发态和基态的统计权重,激发态 原子数Nj与基态原子数No之比较小,<1%. 可以用基态原子数 代表待测元素的原子总数。公式右边除温度T外,都是常数 。T一定,比值一定。 k T h j k T E j k T E E j j e P P e P P e P P N N − j − − − = = = 0 0 0 0 0
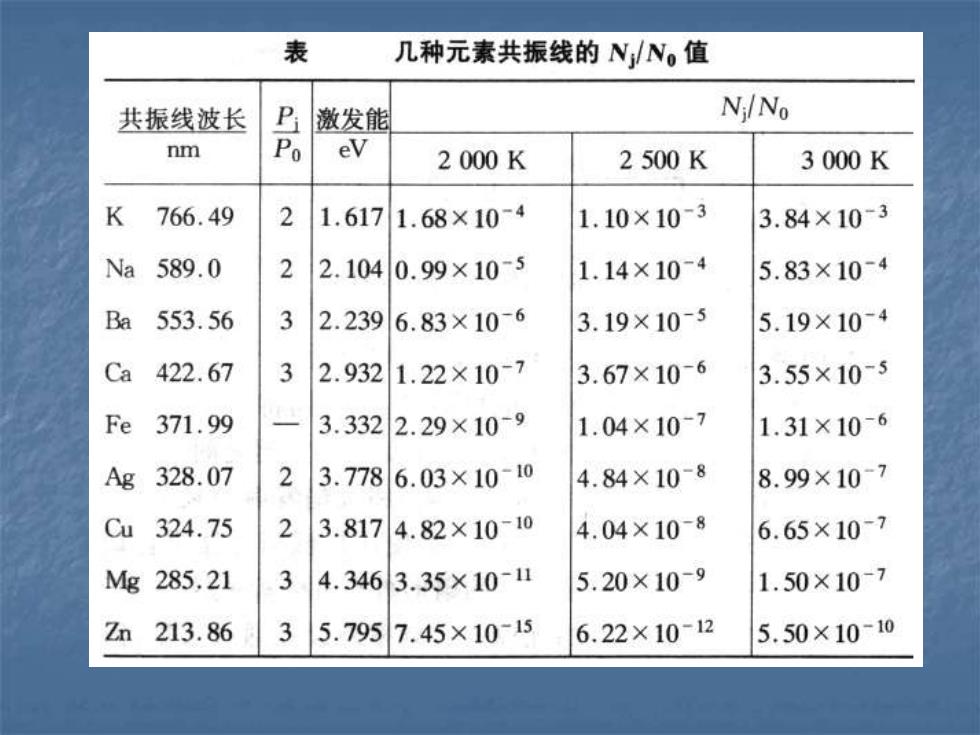
表 几种元素共振线的N/N。值 共振线波长 激发能 Ni/No nm Po eV 2000K 2500K 3000K K 766.49 2 1.617 1.68×10-4 1.10×10-3 3.84×103 Na 589.0 2 2.1040.99×10-5 1.14×10-4 5.83×10-4 Ba 553.56 3 2.2396.83×10-6 3.19×10-5 5.19×10-4 Ca 422.67 3 2.9321.22×10-7 3.67×10-6 3.55×10-5 Fe 371.99 3.332 2.29×109 1.04×107 1.31×10-6 Ag 328.07 2 3.7786.03×1010 4.84×10-8 8.99×10-7 Cu 324.75 2 3.817 4.82×10-10 4.04×10-8 6.65×10-7 Mg 285.21 3 4.346 3.35×10-1 5.20×10-9 1.50×10-7 Zn 213.86 3 5.795 7.45×10-15 6.22×10-12 5.50×10-10

六、定量基础 I=Ioe-Kob 当使用锐线光源时,可用瓜代替K,则: 4=g号-05以,b=04B422g N。·fb △yD me 峰值吸收系数: K。=0.4342nlm2 N。f △vD mc A=kNob Vi OcNo∝e (No激发态原子数,N基态原子数,c待测元素浓度) 所以:A=lg(Io/0=K'c
六、定量基础 峰值吸收系数: 当使用锐线光源时,可用K0代替Kv,则: A = k N0 b N0 ∝N∝c ( N0激发态原子数,N基态原子数,c 待测元素浓度) 所以:A=lg(IO/I)=K' c N f b mc e v K b I I A D = = = 0 2 0 0 2 π ln 2 lg 0.434 0.434 K b t I I e − = 0 N f mc e v K D = 0 2 0 2 π ln 2 0.434