
讲 稿 第一章 物质的状态、溶液和胶体 第二章物质的状态、溶液和胶体 (大学时) 教 案 一、在日常生活和生产实践中,经常可以碰到像泥浆、牛奶、海水等这样一些混合系统,这些系 统是由一种或多种物质分散在其他一种物质中所构成的,我们把这些系统称为分散系。分散系由分散 质和分散剂两部分构成,所谓分散质就是被分散的物质,容纳(或分散)分散质的物质称为分散剂。 第一次课(2学时,下同) 分散质处于分割成粒子的不连续状态,而分散剂则处于连续的状态。在分散系内,分散质和分散剂可 以是固体、液体或气体,故按分散质和分散剂的聚集状态分类,分散系可以有9种,见表11。 主要内容: 生物体内的各种生理、生化反应都是在液体介质中进行的。按照分散质粒子直径大小不同,也常把 1、分散体系的分类 液态分散系分为三类,见表1-2。 表1一2按分散质粒子大小分类的各种分散系 2、溶液的组成标度 以上三种分散系之间虽然有明显的区别,但没有明显的界线,三者之间的过渡是渐变的,某些系 3、蒸气压 4、稀溶液的依激性 类型 粒子直径/nm 分散系名称 主要特征 分子、离子 真溶液 最魏定,扩散快,能透过被纸及半透膜,对光 单 <1 分散系 散射极弱 很稳定,扩散慢,能透过滤纸,不能透过半透 系 1.1分散体系的分类 高分子溶液 膜,光散射弱,粘度大 胶体 1-100 分散系 镜定,扩散慢,能透过滤纸,不能透过半透 1、相:物理性质和化学性质完全相同, 溶胶 膜,光散射强 相 乳状液 不稳定,扩散慢,不能透过越纸及半透膜,无 相与相之间有界面。 粗分散系 >100 统 悬浊液 光散射 单相体系, 统可以同时表现出两种或者三种分散系的性质,因此以分散质粒子直径的大小作为分散系分类的依据 多相体系。 是相对的。在日常生活、科学实验及工农业生产中接触最多的一类分散系是溶液,因此,掌握有关溶 2、分散系=分散质+分散剂 液的基础知识对农业科技工作者来说有着重要的意义
1 第一章 物质的状态、溶液和胶体 (六学时) 教 案 第一次课(2 学时,下同) 主要内容: 1、 分散体系的分类 2、 溶液的组成标度 3、 蒸气压 4、 稀溶液的依数性 1.1 分散体系的分类 1、相:物理性质和化学性质完全相同, 相与相之间有界面。 单相体系, 多相体系。 2、分散系= 分散质 + 分散剂 讲 稿 第二章 物质的状态、溶液和胶体 一、在日常生活和生产实践中,经常可以碰到像泥浆、牛奶、海水等这样一些混合系统,这些系 统是由一种或多种物质分散在其他一种物质中所构成的,我们把这些系统称为分散系。分散系由分散 质和分散剂两部分构成,所谓分散质就是被分散的物质,容纳(或分散)分散质的物质称为分散剂。 分散质处于分割成粒子的不连续状态,而分散剂则处于连续的状态。在分散系内,分散质和分散剂可 以是固体、液体或气体,故按分散质和分散剂的聚集状态分类,分散系可以有 9 种,见表 1-1。 生物体内的各种生理、生化反应都是在液体介质中进行的。按照分散质粒子直径大小不同,也常把 液态分散系分为三类,见表 1-2。 表 1—2 按分散质粒子大小分类的各种分散系 以上三种分散系之间虽然有明显的区别,但没有明显的界线,三者之间的过渡是渐变的,某些系 统可以同时表现出两种或者三种分散系的性质,因此以分散质粒子直径的大小作为分散系分类的依据 是相对的。在日常生活、科学实验及工农业生产中接触最多的一类分散系是溶液,因此,掌握有关溶 液的基础知识对农业科技工作者来说有着重要的意义

分散系的分类:(依分散质颗粒大小分) 二、溶液的组成标度 真溶液:d<lnm单相体系 溶液的组成常用浓度表示,浓度是指溶液中溶质的含量,其表示方法可分为两大类,一类是用溶 质和溶剂的相对量表示,另一类是用溶质和溶液的相对量表示。由于溶质、溶剂或溶液使用的单位不 胶体溶液:1nm<d<100nm 同、浓度的表示方法也不同。 ①溶胶多相体系 ①物质的量浓度:单位体积溶液中所含溶质B的物质的量,符号用cB表示。常用单位为molL。 ②高分子溶液单相体系 CB= 粗分散系:d>100nm多相体系 “物质的量”是国际单位(S1)制中的基本物理量之一,它表示系统中所含基本单元的数量,用符号“” 1.2溶液的组成标度 表示,单位为mo”,叫做“摩尔”。国际计量大会正式通过的物质的量的单位“摩尔的定义为:摩尔 是一系统的物质的量,该系统中所包含的基本单元与0.012kg12C的原子数目相等。在使用摩尔时,应 (溶质/溶剂 溶质/溶液) 指明基本单元。这里所谓的基本单元可以是分子、离子、原子及其它粒子,或这些粒子的特定组合。 1.2.1B的物质的量浓度 基本单元要求用加圆括号的化学式(或化学式的组合)表示,而不宜用中文名称。例如,“1摩尔硫酸” Ca na/V 单位:mol·L 的含意就不确切,应该表示为molH.s0或n出S0mo.同一系统2比S0,和2S0,均可 作基本单元,则相同质量的疏酸的物质的量之间有以下关系: 基本单元:1mol指与0.012Kg2℃所含的 n(H2SO4)=m(1/2 H2SO4)=2n(2 H2SO4) 原子数(6.023×102)相同的任何化学基本 可见,基本单元的选择是任意的,既可以是实际存在的,也可以根据需要人为设定。又如,(KMO4)=O.1 单元(分子,原子、离子等等), molL与cd二KMnO)=0.1molL的两个溶液,它们浓度数值虽然相同,但是,它们所表示1L溶液 所含KMnO4的质量是不同的,分别为15.8g与3.16g 1.2.2溶质B的质量物质的量浓度 ②质量摩尔浓度: ba na/m 每千克溶剂中所含溶质的物质的量,用符号b加表示,单位是mol·kg。 单位:mol·Kg 与温度无关系 b。=”a mA 由于物质的质量不受温度的影响,所以,溶液的质量摩尔浓度与温度无关。 2
2 分散系的分类:(依分散质颗粒大小分) 真溶液: d<1nm 单相体系 胶体溶液:1nm<d<100nm ① 溶胶 多相体系 ② 高分子溶液 单相体系 粗分散系:d>100nm 多相体系 1.2 溶液的组成标度 ( 溶质/溶剂 溶质/溶液) 1.2.1 B 的物质的量浓度 CB = nB/V 单位: mol·L -1 基本单元: 1mol 指与 0.012Kg12C 所含的 原子数(6.023×1023)相同的任何化学基本 单元(分子,原子、离子等等), 1.2.2 溶质 B 的质量物质的量浓度 bB = nB/mA 单位: mol·Kg-1 与温度无关系 二、溶液的组成标度 溶液的组成常用浓度表示,浓度是指溶液中溶质的含量,其表示方法可分为两大类,一类是用溶 质和溶剂的相对量表示,另一类是用溶质和溶液的相对量表示。由于溶质、溶剂或溶液使用的单位不 同、浓度的表示方法也不同。 ①物质的量浓度:单位体积溶液中所含溶质 B 的物质的量,符号用 cB表示。常用单位为 mol·L -1。 V n c B B = “物质的量”是国际单位(SI)制中的基本物理量之一,它表示系统中所含基本单元的数量,用符号“n” 表示,单位为“mol”,叫做“摩尔”。国际计量大会正式通过的物质的量的单位“摩尔”的定义为:摩尔 是一系统的物质的量,该系统中所包含的基本单元与 0.012kg12C 的原子数目相等。在使用摩尔时,应 指明基本单元。这里所谓的基本单元可以是分子、离子、原子及其它粒子,或这些粒子的特定组合。 基本单元要求用加圆括号的化学式(或化学式的组合)表示,而不宜用中文名称。例如,“1 摩尔硫酸” 的含意就不确切,应该表示为 1 molH2SO4或 n(H2SO4) = 1 mol。同一系统 2 1 H2SO4 和 2 H2SO4 均可 作基本单元,则相同质量的硫酸的物质的量之间有以下关系: n(H2SO4) = 2 1 n(1/2 H2SO4) = 2n(2 H2SO4) 可见,基本单元的选择是任意的,既可以是实际存在的,也可以根据需要人为设定。又如,c(KMnO4)=0.1 mol∙L-1 与 c( 5 1 KMnO4)=0.1 mol∙L-1 的两个溶液,它们浓度数值虽然相同,但是,它们所表示 1 L 溶液 所含 KMnO4 的质量是不同的,分别为 15.8g 与 3.16g. ②质量摩尔浓度: 每千克溶剂中所含溶质的物质的量,用符号 bB表示,单位是 mol·kg-1。 A B B m n b = 由于物质的质量不受温度的影响,所以,溶液的质量摩尔浓度与温度无关

例题1-4将0.27gKC1晶体溶于100g水中,计 ③摩尔分数: 算所得溶液中KCI的质量摩尔浓度。 溶液中某组分1的物质的量(m)占溶液总物质的量(n)的分数,用符号X,表示,单位为1。 解:KC1的摩尔质量为74.5gmol。 b(KCI)= n(KCI) m(H,O) 0.27g74.5gmol- 对于一个双组分的溶液系统来说,溶质的物质的量分数与溶剂的物质的量分数分别为: 0.10kg =0.036mol.kg- XB= X1=- nA XA+X8=1 n+ns +ng 1.2.3B的摩尔分数x单位:1 若将这个关系推广到任何一个多组分系统中,则 ∑x=1 对二组分:Xg=n/n X=nu/n ④质量分数: Xa+X=1 溶液中某组分B的质量(m)占溶液总质量(m)的分数,用符号o表示,单位为l。 对多组分:∑XB=1 0。÷e 1.2.4B的质量分数⊙ 三、稀溶液的通性 w me/m 单位:1 溶液的某些性质与溶液中溶质的本性有关,如溶液的颜色、密度、酸碱性和导电性等:对于稀 1.2.5几种溶液组成标度之间的关系 溶液,另一类性质则与溶液中溶质的独立质点数有关,而与溶质本身性质无关,如溶液的蒸气压下降、 (1)物质的量浓度(C)与质量分数(0) 凝固点降低、沸点升高和渗透压等。后一类性质称为稀溶液的通性,或者称为依数性。 Cg=n/N=m/N·V=mes·m/p=op/M
3 例题 1-4 将 0.27gKCl 晶体溶于 100g 水中,计 算所得溶液中 KCl 的质量摩尔浓度。 解: KCl 的摩尔质量为 74.5g∙mol-1。 1 2 0.036mol kg 0.10kg 0.27g/74.5g mol (H O) (KCl) (KCl) 1 − = = = − m n b 1.2.3 B 的摩尔分数 χ 单位:1 对二组分:χB = nB/n χA= nA/n χB + χA= 1 对多组分:∑χB = 1 1.2.4 B 的质量分数 ω ω = mB/m 单位:1 1.2.5 几种溶液组成标度之间的关系 ⑴ 物质的量浓度(CB)与质量分数(ω) CB = nB/V = mB/NB·V = mB/MB·m/ρ=ωρ/ MB ③摩尔分数: 溶液中某组分 i 的物质的量( ni )占溶液总物质的量 ( n )的分数,用符号 i 表示,单位为 1。 n n xB B = 对于一个双组分的溶液系统来说,溶质的物质的量分数与溶剂的物质的量分数分别为: 若将这个关系推广到任何一个多组分系统中,则 ④质量分数: 溶液中某组分 B 的质量 ( mB ) 占溶液总质量 ( m ) 的分数,用符号 B 表示,单位为 l。 m mB B = 三、 稀溶液的通性 溶液的某些性质与溶液中溶质的本性有关,如溶液的颜色、密度、酸碱性和导电性等;对于稀 溶液,另一类性质则与溶液中溶质的独立质点数有关,而与溶质本身性质无关,如溶液的蒸气压下降、 凝固点降低、沸点升高和渗透压等。后一类性质称为稀溶液的通性,或者称为依数性。 A B B B n n n x + = A B A A n n n x + = xA + xB =1 B = 1 B x
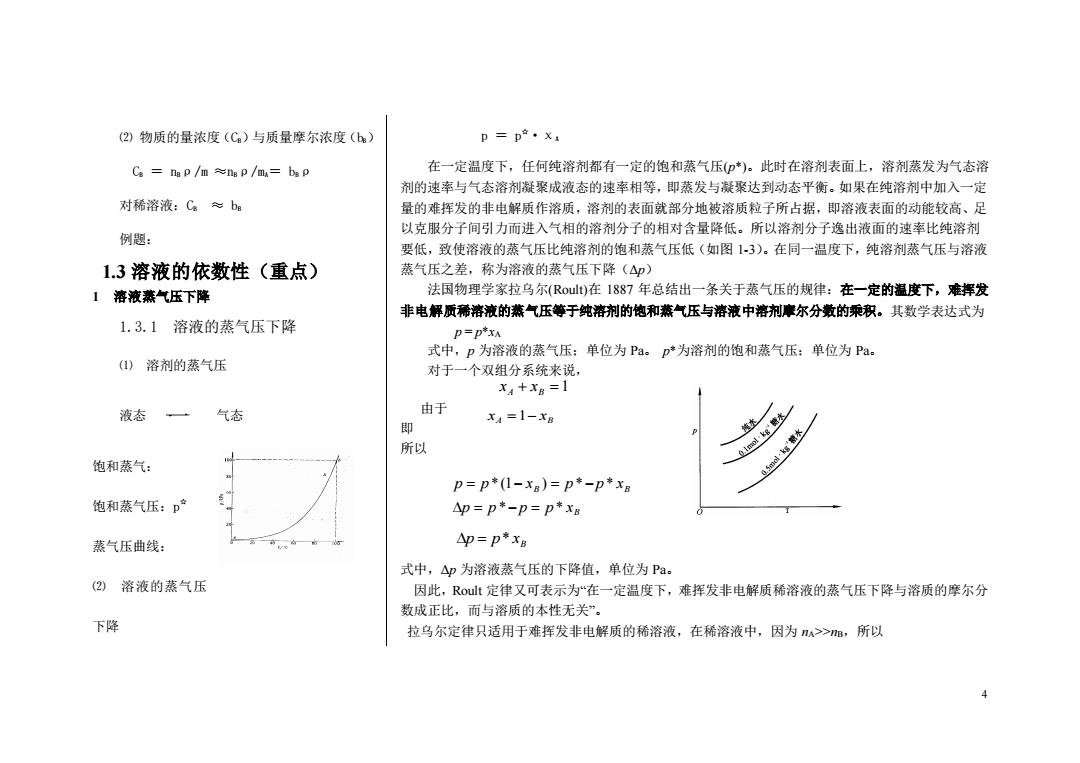
(2)物质的量浓度(Ca)与质量摩尔浓度(b) p=p·Xa Ca=nep/m≈ngp/mu=bsp 在一定温度下,任何纯溶剂都有一定的饱和蒸气压(*)。此时在溶剂表面上,溶剂蒸发为气态溶 剂的速率与气态溶剂凝聚成液态的速率相等,即蒸发与凝聚达到动态平衡。如果在纯溶剂中加入一定 对稀溶液:C。≈bs 量的难挥发的非电解质作溶质,溶剂的表面就部分地被溶质粒子所占据,即溶液表面的动能较高、足 以克服分子间引力而进入气相的溶剂分子的相对含量降低。所以溶剂分子逸出液面的速率比纯溶剂 例题: 要低,致使溶液的蒸气压比纯溶剂的饱和蒸气压低(如图13)。在同一温度下,纯溶剂蒸气压与溶液 1.3溶液的依数性(重点) 蒸气压之差,称为溶液的蒸气压下降(△p) 1溶液蒸气压下降 法国物理学家拉乌尔(Rout)在1887年总结出一条关于蒸气压的规律:在一定的温度下,难挥发 非电解质稀溶液的蒸气压等于纯溶剂的饱和蒸气压与溶液中溶剂摩尔分数的乘积。其数学表达式为 1.3.1溶液的蒸气压下降 p=px 式中,p为溶液的蒸气压:单位为Pa。p*为溶剂的饱和蒸气压:单位为Pa。 (1)溶剂的蒸气压 对于一个双组分系统来说, xA+X8=1 液态 气态 由于 X4=1-XB 即 所以 饱和蒸气: p=p*(1-xB)=p*-p*x 饱和蒸气压:p产 △p=p*-p=p*x 蒸气压曲线: △p=p*xB 式中,△p为溶液蒸气压的下降值,单位为Pa。 (2)溶液的蒸气压 因此,Rout定律又可表示为“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶质的摩尔分 数成正比,而与溶质的本性无关”。 下降 拉乌尔定律只适用于难挥发非电解质的稀溶液,在稀溶液中,因为>>m,所以 4
4 ⑵ 物质的量浓度(CB)与质量摩尔浓度(bB) CB = nBρ/m ≈nBρ/mA= bBρ 对稀溶液:CB ≈ bB 例题: 1.3 溶液的依数性(重点) 1 溶液蒸气压下降 1.3.1 溶液的蒸气压下降 ⑴ 溶剂的蒸气压 液态 气态 饱和蒸气: 饱和蒸气压:p ☆ 蒸气压曲线: ⑵ 溶液的蒸气压 下降 p = p ☆·χA 在一定温度下,任何纯溶剂都有一定的饱和蒸气压(p*)。此时在溶剂表面上,溶剂蒸发为气态溶 剂的速率与气态溶剂凝聚成液态的速率相等,即蒸发与凝聚达到动态平衡。如果在纯溶剂中加入一定 量的难挥发的非电解质作溶质,溶剂的表面就部分地被溶质粒子所占据,即溶液表面的动能较高、足 以克服分子间引力而进入气相的溶剂分子的相对含量降低。所以溶剂分子逸出液面的速率比纯溶剂 要低,致使溶液的蒸气压比纯溶剂的饱和蒸气压低(如图 1-3)。在同一温度下,纯溶剂蒸气压与溶液 蒸气压之差,称为溶液的蒸气压下降(Δp) 法国物理学家拉乌尔(Roult)在 1887 年总结出一条关于蒸气压的规律:在一定的温度下,难挥发 非电解质稀溶液的蒸气压等于纯溶剂的饱和蒸气压与溶液中溶剂摩尔分数的乘积。其数学表达式为 p = p*xA 式中,p 为溶液的蒸气压;单位为 Pa。 p*为溶剂的饱和蒸气压;单位为 Pa。 对于一个双组分系统来说, 由于 即 所以 B p = p* x 式中,Δp 为溶液蒸气压的下降值,单位为 Pa。 因此,Roult 定律又可表示为“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶质的摩尔分 数成正比,而与溶质的本性无关”。 拉乌尔定律只适用于难挥发非电解质的稀溶液,在稀溶液中,因为 nA>>nB,所以 xA + xB =1 A B x =1− x B B B p p p p x p p x p p x * * *(1 ) * * = − = = − = −
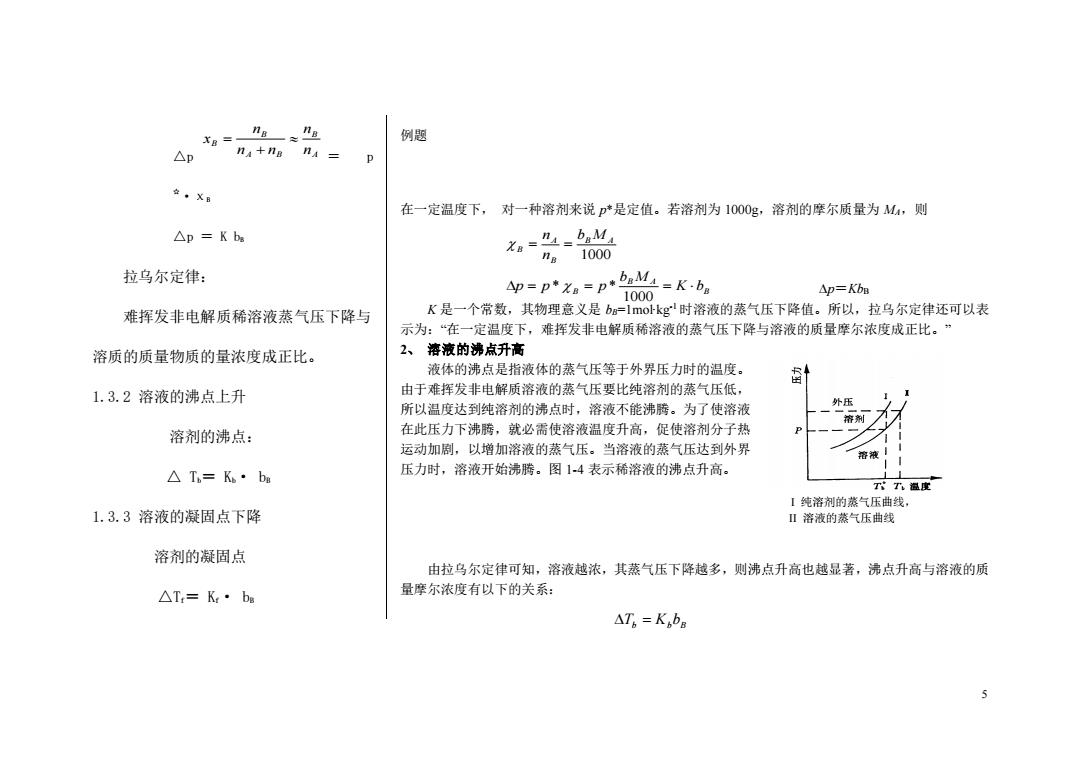
ng≈” 例题 △p na+ng n 在·XB 在一定温度下,对一种溶剂来说p*是定值。若溶剂为1000g,溶剂的摩尔质量为M,则 △p=Kbs a-”=bM ng1000 拉乌尔定律: p=p*xB=p*bM=K-b。 1000 Ap=KbB 难挥发非电解质稀溶液蒸气压下降与 K是一个常数,其物理意义是b=1 mol-kg时溶液的蒸气压下降值。所以,拉乌尔定律还可以表 示为:“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶液的质量摩尔浓度成正比。” 溶质的质量物质的量浓度成正比。 2、溶液的沸点升高 液体的沸点是指液体的蒸气压等于外界压力时的温度。 1.3.2溶液的沸点上升 由于难挥发非电解质溶液的蒸气压要比纯溶剂的蒸气压低, 所以温度达到纯溶剂的沸点时,溶液不能沸腾。为了使溶液 外压 溶剂 溶剂的沸点: 在此压力下沸腾,就必需使溶液温度升高,促使溶剂分子热 运动加剧,以增加溶液的蒸气压。当溶液的蒸气压达到外界 △T=K·bg 压力时,溶液开始沸腾。图14表示稀溶液的沸点升高。 TT温度 【纯溶剂的蒸气压曲线, 1.3.3溶液的凝固点下降 Ⅱ溶液的蒸气压曲线 溶剂的凝固点 由拉乌尔定律可知,溶液越浓,其蒸气压下降越多,则沸点升高也越显著,沸点升高与溶液的质 △T=K:·be 量摩尔浓度有以下的关系: △T6=KbB 5
5 △p = p ☆·χB △p = K bB 拉乌尔定律: 难挥发非电解质稀溶液蒸气压下降与 溶质的质量物质的量浓度成正比。 1.3.2 溶液的沸点上升 溶剂的沸点: △ Tb= Kb· bB 1.3.3 溶液的凝固点下降 溶剂的凝固点 △Tf= Kf· bB 例题 在一定温度下, 对一种溶剂来说 p*是定值。若溶剂为 1000g,溶剂的摩尔质量为 MA,则 p=KbB K 是一个常数,其物理意义是 bB=1mol∙kg-1 时溶液的蒸气压下降值。所以,拉乌尔定律还可以表 示为:“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶液的质量摩尔浓度成正比。” 2、 溶液的沸点升高 液体的沸点是指液体的蒸气压等于外界压力时的温度。 由于难挥发非电解质溶液的蒸气压要比纯溶剂的蒸气压低, 所以温度达到纯溶剂的沸点时,溶液不能沸腾。为了使溶液 在此压力下沸腾,就必需使溶液温度升高,促使溶剂分子热 运动加剧,以增加溶液的蒸气压。当溶液的蒸气压达到外界 压力时,溶液开始沸腾。图 1-4 表示稀溶液的沸点升高。 由拉乌尔定律可知,溶液越浓,其蒸气压下降越多,则沸点升高也越显著,沸点升高与溶液的质 量摩尔浓度有以下的关系: I 纯溶剂的蒸气压曲线, II 溶液的蒸气压曲线 B B A B B A B A B K b b M p p p b M n n = = = = = 1000 * * 1000 A B A B B B n n n n n x + = Tb = KbbB