
2.电子导电:金属 Debye模型和晶格振动 >把晶格振动看成弹性波在晶体内传播 >这些波也是量子化的,其量子化最小单元称 为“声子”,类比于电磁波的“光子” > 假设存在最大的振动频率ym,并且以此定义 一个关键参数德拜温度OD=hvmax/kg: T>⊙,则声子被激发,可以用经 典理论近似,此时Cy≈3R T<⑨,则声子“冻结”,需要 (a) 用量子理论解决问题,此时Cyc T(德拜T律); (b) >在发现电子相互作用对热容的贡献 之前,德拜律对低温下晶体热容做 AAAAAAA 出了最精确的表述
2.电子导电:金属 11 Debye模型和晶格振动 ➢ 把晶格振动看成弹性波在晶体内传播 ➢ 这些波也是量子化的,其量子化最小单元称 为“声子”,类比于电磁波的“光子” ➢ 假设存在最大的振动频率max,并且以此定义 一个关键参数德拜温度𝜣𝑫 = 𝒉𝝂𝒎𝒂𝒙/𝒌𝑩: • T > D,则声子被激发,可以用经 典理论近似,此时CV 3R • T << D,则声子“冻结”,需要 用量子理论解决问题,此时CV T 3(德拜T 3律); ➢ 在发现电子相互作用对热容的贡献 之前,德拜T 3律对低温下晶体热容做 出了最精确的表述
2.电子导电:金属 Debye模型和晶格振动 >不足之处: 未考虑电子电子相互作用,导致T< 2K时T律失效 实际上O,会随温度变化,但Debye模 型并未考虑这一点 假设晶体振动有一个最高频率,而实 际上并没有 >但是,Debye模型仍然在很大温度区间 (a) 内成功解释了很多现象,而Debye温度 对于研究电导率-温度的关系也仍有很重 (b) 要的指导意义。 A
2.电子导电:金属 12 Debye模型和晶格振动 ➢ 不足之处: • 未考虑电子-电子相互作用,导致T < 2K时T 3律失效 • 实际上D会随温度变化,但Debye模 型并未考虑这一点 • 假设晶体振动有一个最高频率,而实 际上并没有 ➢ 但是,Debye模型仍然在很大温度区间 内成功解释了很多现象,而Debye温度 对于研究电导率-温度的关系也仍有很重 要的指导意义
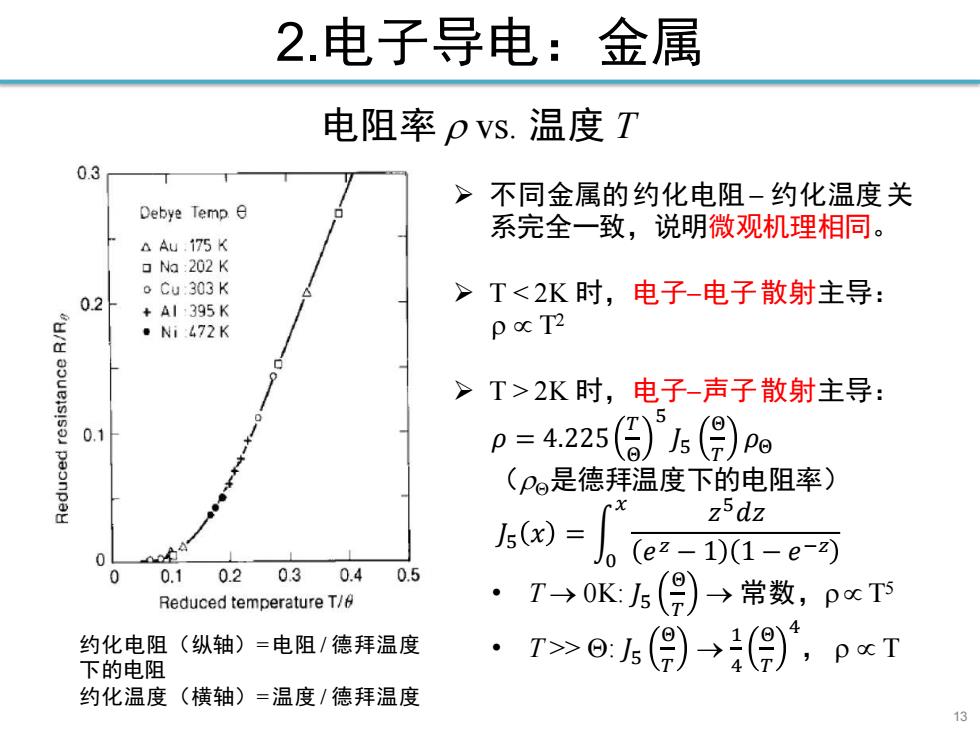
2.电子导电:金属 电阻率pvs.温度T 03 >不同金属的约化电阻-约化温度关 Debye Temp e 系完全一致,说明微观机理相同。 △Au:175K ▣Na202K o Cu:303 K 0.2 >T<2K时,电子-电子散射主导: +A1395K ·Ni472K p oc T2 正 >T>2K时,电子-声子散射主导: 0.1 p=4225(6(月)g (p阳是德拜温度下的电阻率) X z5dz 0 04 j5=0e2 1)(1-e-2) 0 0.10.2030.40.5 Reduced temperature T/ T→0K5()→常数,pxT5 约化电阻(纵轴)=电阻/德拜温度 下的电阻 T>05(月)→(),pcT 约化温度(横轴)=温度/德拜温度
2.电子导电:金属 13 ➢ 不同金属的约化电阻− 约化温度关 系完全一致,说明微观机理相同。 ➢ T < 2K 时,电子−电子散射主导: T2 ➢ T > 2K 时,电子−声子散射主导: 𝜌 = 4.225 𝑇 Θ 5 𝐽5 Θ 𝑇 𝜌Θ (是德拜温度下的电阻率) 𝐽5 𝑥 = න 0 𝑥 𝑧 5𝑑𝑧 𝑒 𝑧 − 1 1 − 𝑒 −𝑧 • T → 0K: 𝐽5 Θ 𝑇 → 常数, T5 • T >> : 𝐽5 Θ 𝑇 → 1 4 Θ 𝑇 4 , T 电阻率 vs. 温度 T 约化电阻(纵轴)= 电阻 / 德拜温度 下的电阻 约化温度(横轴)= 温度 / 德拜温度