
一、 卡诺循环 卡诺(Carnet)):法国工程师,于1824年发表了《关于火的动力之见解》一书,书中 介绍了一种在两个热源间工作的可逆热机,即卡诺热机。卡诺热机以理想气体为工作 物质,从高温T热源吸收Q的热量,一部分通过理想热机用来对外做功W,另一部 分Q的热量放给低温T。热源。这种循环称为卡诺循环。整个循环过程均不存在摩擦 力,卡诺热机的循环由两个绝热过程和两个等温过程组成。 热机是将热能转变为功的一种机械,一般的热机均在两个不同温度的热源之间工 作,热机从高温热源吸取热量,但此热量不可能全部转化为功,只能一部分转化为功, 而另一部分则成为废热传给了等温热源常见的热机如:汽车,飞机,轮船,火力发电机等 理想气体的卡诺循环:工作物质(1mol理想气体)1mol理想气体的卡诺循环在 pV图上可以分为四步: 1.卡若循环的热和功 A PiV1 人 (I)等温可逆膨胀:A→B P2V2 体系与高温T2(T)热源接触,从环境中 Q2 吸收热量Q,状态从A变化到B由于理想 D 气体仅是温度的函数,△U=O,体系吸收的 Q:Ti AC P3V3 热量全部转化为功。 卡若循环 2=-W 所以体系必须先从环境吸收Q2的热后,全部以 功的形式来增加体积,即对环境做功: 以=-r-n哈 (2)绝热可逆膨胀B→C 体系离开高温热源,与环境隔绝,Q,=O,状态从B变化到C,体系消耗内能对外做功, 温度由T2降至T,则 W2=AU2 nCY(Ti-T) (3)等温可逆压缩过程C→D -11-
- 11 - 一、 卡诺循环 卡诺(Carnet): 法国工程师, 于 1824 年发表了《关于火的动力之见解》一书, 书中 介绍了一种在两个热源间工作的可逆热机, 即卡诺热机。卡诺热机以理想气体为工作 物质,从高温 Th热源吸收 Qh的热量,一部分通过理想热机用来对外做功 W,另一部 分 Qc 的热量放给低温 Tc 热源。这种循环称为卡诺循环。整个循环过程均不存在摩擦 力, 卡诺热机的循环由两个绝热过程和两个等温过程组成。 热机是将热能转变为功的一种机械, 一般的热机均在两个不同温度的热源之间工 作, 热机从高温热源吸取热量, 但此热量不可能全部转化为功, 只能一部分转化为功, 而另一部分则成为废热传给了等温热源.常见的热机如: 汽车,飞机,轮船,火力发电机等. 理想气体的卡诺循环:工作物质(1mol 理想气体)1mol 理想气体的卡诺循环在 pV 图上可以分为四步: 1. 卡若循环的热和功 ⑴等温可逆膨胀: A B → 体系与高温 T2(Th)热源接触,从环境中 吸收热量 Q2,状态从 A 变化到 B 由于理想 气体仅是温度的函数,△U1=0,体系吸收的 热量全部转化为功。 Q W 2 1 = − 所以体系必须先从环境吸收 Q2 的热后,全部以 功的形式来增加体积,即对环境做功: 2 1 2 1 1 ln V V V W PdV nRT V = − = − ⑵绝热可逆膨胀 B C → 体系离开高温热源,与环境隔绝,Q2 =0,状态从 B 变化到 C,体系消耗内能对外做功, 温度由 T2 降至 T1,则 W U nC T T 2 2 1 2 = = − V ( ) ⑶等温可逆压缩过程 C D →

体系与低温热源T1(T)接触,等温压缩,体系状态从C变化到D,等温过程△U,=O, 体系所得功全部转化为热,传给环境。 W,=-JPd=-nRT V (4)绝热可逆压缩过程D→A 体系离开低温热源,与环境隔离,Q,=0,状态从D便回到A,体系所作的功全部用 于体系的内能增加,温度由T升至T2:W4=△U,=nC,(T2-T) 以上四个过程构成一个可逆循环,体系对环境所作的功相当于四边形ABCD所围面 积,循环一周后体系恢复原状,则△U=0,Q=Q,+Q,=W 功:W=形+形+形+形三-RTn 即:W=-RTn上-RTn当 由于过程和过程是绝热可逆过程,使用绝热可逆过程方程式: 过程2:T=TY 过程4:T,V=TV-1 两式相除得: 业- VV 因此,理想气体在卡若循环中所作的功为:取=RG-)加宁 对整个循环: -12-
- 12 - 体系与低温热源 T1(Tc)接触,等温压缩,体系状态从 C 变化到 D ,等温过程△U3 =0, 体系所得功全部转化为热,传给环境。 4 3 4 3 3 ln V V V W PdV nRT V = − = − ⑷绝热可逆压缩过程 D A → 体系离开低温热源,与环境隔离,Q4 =0 ,状态从 D 便回到 A,体系所作的功全部用 于体系的内能增加,温度由 T1 升至 T2:W U nC T T 4 4 2 1 = = − V ( ) 以上四个过程构成一个可逆循环,体系对环境所作的功相当于四边形 ABCD 所围面 积 ,循环一周后体系恢复原状,则△U=0 ,Q=Q1 +Q2 =-W 体系所作的总功 : 2 4 1 2 3 4 1 2 1 3 ln ln V V W W W W W RT RT V V = + + + = − − − 即: 2 4 1 2 1 3 ln ln V V W RT RT V V = − − − 由于过程和过程是绝热可逆过程,使用绝热可逆过程方程式 : 过程 2: 1 1 T V TV 2 2 1 3 − − = 过程 4: 1 1 T V TV 2 1 1 4 − − = 两式相除得: 2 3 1 4 V V V V = 因此,理想气体在卡若循环中所作的功为: ( ) 1 2 1 2 ln V W nR T T V = − 对整个循环:
4e3) Bg2,3,T) D04,E) ,3,T) T d b △U=0 Q6:体系吸收地热量,为正值 O=0,+0 Q。:体系放出的热量,为负值 W=W+WW,和W对消 ABCD曲线所围面积为热机所做的功。 w=nRC-T。)ln2 整个循环过程中,体系从环境所吸收的热为 =2+0=-W-R(T,-T)In 由于T2>T和V2>V1,所以-W>0,表明整个循环过程是体系从高温热源吸收热后,对环 境做功。 2.卡若热机效率 热机在循环过程中所作的功与他从高温热源所吸收的热的比值称为热机的转换系数, 也称为热机效率。用η表示。 tn) =1- Te Th-Te -nRn吃) 7=”-2+是Q<0) -13-
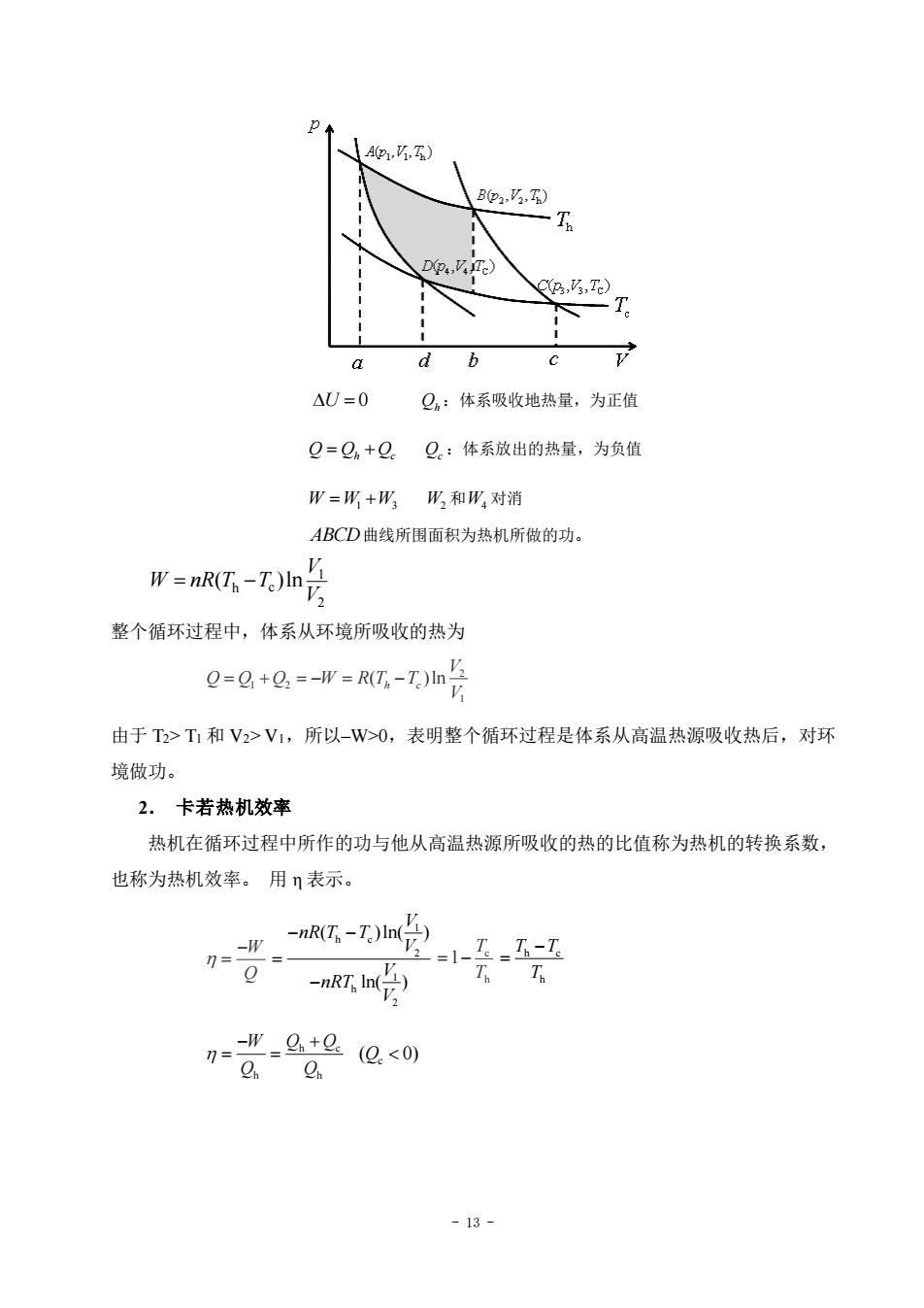
- 13 - = U 0 Qh :体系吸收地热量,为正值 Q Q Q = +h c Qc :体系放出的热量,为负值 W W W = +1 3 W2 和 W4 对消 ABCD 曲线所围面积为热机所做的功。 1 h c 2 ( )ln V W nR T T V = − 整个循环过程中,体系从环境所吸收的热为 2 1 2 1 ( )ln h c V Q Q Q W R T T V = + = − = − 由于 T2> T1 和 V2> V1,所以–W>0,表明整个循环过程是体系从高温热源吸收热后,对环 境做功。 2. 卡若热机效率 热机在循环过程中所作的功与他从高温热源所吸收的热的比值称为热机的转换系数, 也称为热机效率。 用 η 表示。 W Q − = 1 h c 2 1 h 2 ( )ln( ) ln( ) V nR T T V V nRT V − − = − c h 1 T T = − h c h T T T − = h c h h W Q Q Q Q − + = = c ( 0) Q

nR(g,-T)n兰 或者: 02 nRT,In T 可见卡诺热机的工作效率只与两个热源温度有关,两个热源的温差越大,热机转换系 数越大,热量的利用也越完全。在等温的循环过程中转换系数等于零,即热一点也不能转 变为功。 实际设计中,通常低温热源就是大气环境,高温热源常用过热蒸汽。如果使用高压过 热蒸汽823K,和特殊的冷凝器283K,转化率可以达到65%,实际转换系数远低于此值。 卡诺循环是热功转换的理想循环,实际上是不可能实现的,但这个循环对热力学来说 是非常重要的,他指出了热功转换的限度,由它可以找出判断过程方向和限度的重要关系 式,这也是下一章我们要解决的问题。 二、卡诺定理 从卡诺循环知,热机的效率小于1,假若热机的效率等于1,也就是说这种机器可以将 从高温热源中吸收的热Q2全部转化为功,这就是第二类永动机可以制得,或说是能从单一 热源取出使之完全变为功,即第二定律不成立,而经验告诉我们热力学第二定律成立,那 么热机的效率小于1,但到底热机的效率最高可达多少? 卡诺认为:工作于两个不同温度之间的所有热机,以卡诺可逆热机的工作效率为最大, 其工作效率只决定于两个热源的温度,与工作物质无关。 或说:所有工作于同温热源和同温冷源之间的热机,其效率都不能超过可逆热机的工 作效率—这就是卡诺原理或卡诺定理。 (一)数学表达 任意热机: n,=9+g 0, 卡诺热机:7n=+_-T+工 102+g,1=|w川 则 7≤1R 或 e+eTi+T 或 9+≤0 2T, T T 上式中7:是任意热机的热机效率, -14-
- 14 - 或者: 1 2 1 2 2 1 2 2 1 2 1 2 1 ( )ln ln V nR T T V T T V T nRT W Q Q V Q Q − − = + = − = = 可见卡诺热机的工作效率只与两个热源温度有关,两个热源的温差越大,热机转换系 数越大,热量的利用也越完全。在等温的循环过程中转换系数等于零,即热一点也不能转 变为功。 实际设计中,通常低温热源就是大气环境,高温热源常用过热蒸汽。如果使用高压过 热蒸汽 823K,和特殊的冷凝器 283K,转化率可以达到 65%,实际转换系数远低于此值。 卡诺循环是热功转换的理想循环,实际上是不可能实现的,但这个循环对热力学来说 是非常重要的,他指出了热功转换的限度,由它可以找出判断过程方向和限度的重要关系 式,这也是下一章我们要解决的问题。 二、卡诺定理 从卡诺循环知,热机的效率小于 1,假若热机的效率等于 1,也就是说这种机器可以将 从高温热源中吸收的热 Q2 全部转化为功,这就是第二类永动机可以制得,或说是能从单一 热源取出使之完全变为功,即第二定律不成立,而经验告诉我们热力学第二定律成立,那 么热机的效率小于 1,但到底热机的效率最高可达多少? 卡诺认为:工作于两个不同温度之间的所有热机,以卡诺可逆热机的工作效率为最大, 其工作效率只决定于两个热源的温度,与工作物质无关。 或说:所有工作于同温热源和同温冷源之间的热机,其效率都不能超过可逆热机的工 作效率——这就是卡诺原理或卡诺定理。 (一)数学表达 任意热机: 2 1 2 Q Q Q I + = 卡诺热机: 2 1 2 2 1 2 T T T Q Q Q R + = + = ︱Q2 +Q1︱=︱W︱ 则 R 或 2 1 2 2 1 2 T T T Q Q Q + + 或 0 2 2 1 1 + T Q T Q 上式中 :是任意热机的热机效率

)r:是可逆热机的热机效率 热温商: 是体系与热源所交换的热量Q与热 高温热源T2 T 源的温度T之比叫热温商。 lwl-Q →|WI-|WRI>0 对卡诺热机:式中等号成立,说明卡诺循 环过程体系的热温商之和等于零: QR(大) Q(小IQrI<|QR| 对不可逆热机:式中不等号成立,说明卡 低温热源工 A:不可逆热机 诺循环过程体系的热温商之和小于零, B:可逆热机 工作时使体系的热温商之和大于零的热机是不存在的, 对卡诺定理的证明:用反证法证明(选讲) 在两热源T1,T2之间有一个卡诺热机R和任意热机I,并假设I的效率比R的效率大, 那么,同样从热源T2吸收了Q2的热时,热机I所作功为WR,将大于热机R所作的功WR, 根据能量守恒定律,Q2-|Q=W,有|QR<|Q|,若将这两个热机联合起来使它们这样 工作,用热机I从热源T2吸收Q2的热,并作功WR,同时放出|QR|的热给T1,然后从 WR的功中取出一部分功对热机R作功驱动其反转,此时R就能从低温热源T吸取QR| 的热,同时有Q2的热传入T2,联合的总结果是:高温热源T2没有任何变化,低温热源损 失了|QR|-|QR|的热量,而环境得到WR-WR的功,因为 若n>nR'则|W|>|WRI,即|W|-|WR|>0,I2|<| 净结果:(1)高温热源无变化 2)联合热机对外作功|W.I一|W。I>0 (3)从低温热源吸收热|Q|-|Q.I>0 两部热机联合结果是从单一热源下吸收|Q。丨一|Q.|的热而对外作功为|W|一 |WR|=|Q|一|Q|。这违背了热力学第二定律。 因此,nR 7=2+坦s4,-g 22 1+9≤1-g 92 (等号可逆,小于不可逆) -15-
- 15 - R:是可逆热机的热机效率 热温商: T Q 是体系与热源所交换的热量 Q 与热 源的温度 T 之比叫热温商。 对卡诺热机:式中等号成立,说明卡诺循 环过程体系的热温商之和等于零; 对不可逆热机:式中不等号成立,说明卡 诺循环过程体系的热温商之和小于零, 工作时使体系的热温商之和大于零的热机是不存在的, 对卡诺定理的证明:用反证法证明 (选讲) 在两热源 T1,T2 之间有一个卡诺热机 R 和任意热机 I,并假设 I 的效率比 R 的效率大, 那么,同样从热源 T2 吸收了 Q2 的热时,热机 I 所作功为 WIR,将大于热机 R 所作的功 WR, 根据能量守恒定律,Q2-│Q1│=W,有│QIR│<│QR│,若将这两个热机联合起来使它们这样 工作,用热机 I 从热源 T2 吸收 Q2 的热,并作功 WIR,同时放出│QIR│的热给 T1,然后从 WIR 的功中取出一部分功对热机 R 作功驱动其反转,此时 R 就能从低温热源 T1 吸取│QIR│ 的热,同时有 Q2 的热传入 T2,联合的总结果是:高温热源 T2 没有任何变化,低温热源损 失了│QR│-│QIR│的热量,而环境得到 WIR-WR的功,因为 若 η Ir >η R,则︱WIr︱>︱WR︱,即︱WIr︱-︱WR︱>0,︱QIr︱<︱QR︱ 净结果: (1)高温热源无变化. (2)联合热机对外作功︱WIr︱-︱WR︱>0 (3)从低温热源吸收热︱QR︱-︱QIr︱>0 两部热机联合结果是从单一热源下吸收︱QR︱-︱QIr︱的热而对外作功为︱WIr︱- ︱WR︱=︱QR︱-︱QIr︱。这违背了热力学第二定律。 因此,η Ir≤ηR (等号可逆,小于不可逆)