
丝姜大字 物理化学游稿 第十二章化学动力学基础(二) (10学时) 物理化学教研室
物理化学讲稿 第十二章 化学动力学基础(二) (10 学时) 物理化学教研室
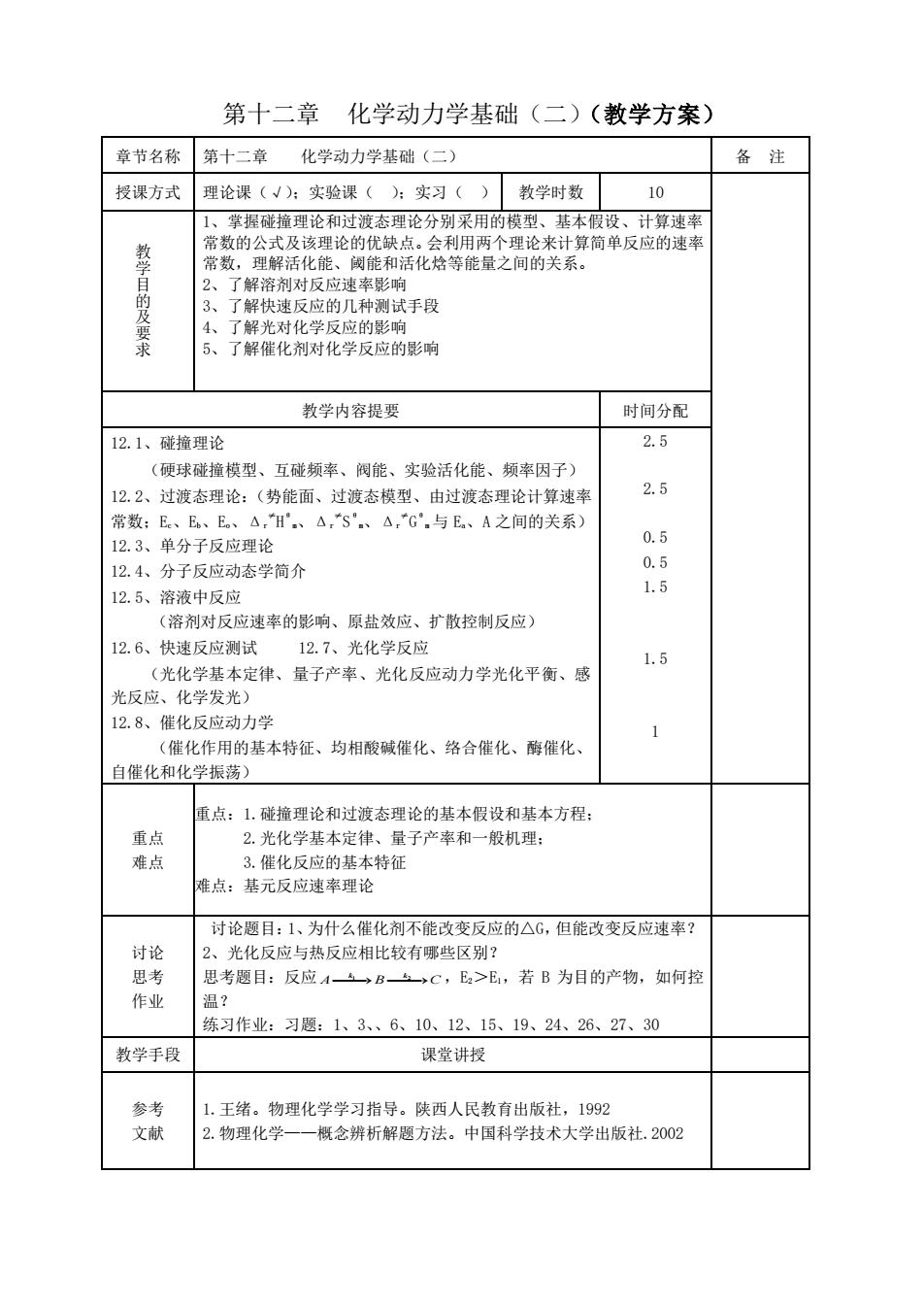
第十二章 化学动力学基础(二)(教学方案) 章节名称 第十二章 化学动力学基础(二) 备注 授课方式 理论课(√):实验课():实习() 教学时数 10 1、 掌握碰撞理论和过渡态理论分别采用的模型、基本假设、计算速率 常数的公式及该理论的优缺点。会利用两个理论来计算简单反应的速率 鏊 常数,理解活化能、阈能和活化焓等能量之间的关系。 目的及要 2、了解溶剂对反应速率影响 3、了解快速反应的几种测试手段 4、了解光对化学反应的影响 5、 了解催化剂对化学反应的影响 教学内容提要 时间分配 12.1、碰撞理论 2.5 (硬球碰撞模型、互碰频率、阀能、实验活化能、频率因子) 12.2、过渡态理论:(势能面、过渡态模型、由过渡态理论计算速率 2.5 常数:Ee、E。、E。、△,H.、△,S.、△C.与E。、A之间的关系) 12.3、单分子反应理论 0.5 12.4、分子反应动态学简介 0.5 12.5、溶液中反应 1.5 (溶剂对反应速率的影响、原盐效应、扩散控制反应) 12.6、快速反应测试 12.7、光化学反应 1.5 (光化学基本定律、量子产率、光化反应动力学光化平衡、感 光反应、化学发光) 12.8、催化反应动力学 (催化作用的基本特征、均相酸碱催化、络合催化、酶催化 自催化和化学振荡) 重点:1.碰撞理论和过渡态理论的基本假设和基本方程: 重点 2.光化学基本定律、量子产率和一般机理: 难点 3.催化反应的基本特征 难点:基元反应速率理论 讨论题目:1、为什么催化剂不能改变反应的△G,但能改变反应速率? 讨论 2、光化反应与热反应相比较有哪些区别? 思考 思考题目:反应ABs>C,E2>E1,若B为目的产物,如何控 作业 温? 练习作业:习题:1、3、6、10、12、15、19、24、26、27、30 教学手段 课堂讲授 参考 1.王绪。物理化学学习指导。陕西人民教育出版社,1992 文献 2.物理化学一一概念辨析解题方法。中国科学技术大学出版社.2002
第十二章 化学动力学基础(二)(教学方案) 章节名称 第十二章 化学动力学基础(二) 备 注 授课方式 理论课(√);实验课( );实习( ) 教学时数 10 教 学 目 的 及 要 求 1、掌握碰撞理论和过渡态理论分别采用的模型、基本假设、计算速率 常数的公式及该理论的优缺点。会利用两个理论来计算简单反应的速率 常数,理解活化能、阈能和活化焓等能量之间的关系。 2、了解溶剂对反应速率影响 3、了解快速反应的几种测试手段 4、了解光对化学反应的影响 5、了解催化剂对化学反应的影响 教学内容提要 时间分配 12.1、碰撞理论 (硬球碰撞模型、互碰频率、阀能、实验活化能、频率因子) 12.2、过渡态理论:(势能面、过渡态模型、由过渡态理论计算速率 常数;Ec、Eb、Eo、Δr ≠ H θ m、Δr ≠ S θ m、Δr ≠ G θ m 与 Ea、A 之间的关系) 12.3、单分子反应理论 12.4、分子反应动态学简介 12.5、溶液中反应 (溶剂对反应速率的影响、原盐效应、扩散控制反应) 12.6、快速反应测试 12.7、光化学反应 (光化学基本定律、量子产率、光化反应动力学光化平衡、感 光反应、化学发光) 12.8、催化反应动力学 (催化作用的基本特征、均相酸碱催化、络合催化、酶催化、 自催化和化学振荡) 2.5 2.5 0.5 0.5 1.5 1.5 1 重点 难点 重点:1.碰撞理论和过渡态理论的基本假设和基本方程; 2.光化学基本定律、量子产率和一般机理; 3.催化反应的基本特征 难点:基元反应速率理论 讨论 思考 作业 讨论题目:1、为什么催化剂不能改变反应的△G,但能改变反应速率? 2、光化反应与热反应相比较有哪些区别? 思考题目:反应 1 2 k k A B C ⎯⎯→ ⎯⎯→ ,E2>E1,若 B 为目的产物,如何控 温? 练习作业:习题:1、3、、6、10、12、15、19、24、26、27、30 教学手段 课堂讲授 参考 文献 1.王绪。物理化学学习指导。陕西人民教育出版社,1992 2.物理化学——概念辨析解题方法。中国科学技术大学出版社.2002

第十二章化学动力学基础(二) 人们在测量了大量反应的速率常数,并对反应速率常数于温度的依赖关系有了相当了 解以后,对于为什么会有这些宏观规律存在必须从理论给予回答。在反应速率理论的发展 过程中,先后形成了碰撞理论、过渡态理论和单分子反应理论等。动力学理论与,发展较 迟。先后形成的碰撞理论、过渡态理论都是20世纪后建立起来的。而且与热力学的经典 理论相比尚有明显不足之处。 速度理论是研究化学反应的速率系数与温度的关系,描述反应过程的动力学性质。 速率理论的共同点:首先选定一个微观模型,用气体分子运动论(碰撞理论)或量子力 学(过渡态理论)的方法,并经过统计平均,导出宏观动力学中速率系数的计算公式。 由于所采用模型的局限性,使计算值与实验值不能完全吻合,还必须引入一些校正因 子,使理论的应用受到一定的限制。 §12.1碰撞理论(Simple Collision theory)(SCT) 碰撞理论是接受了阿伦尼乌斯关于“活化状态”和“活化能”概念的基础上,利用已 经建立起来的气体分子运动论的基础上,在20世纪初由路易斯建立起来的。路易斯把气 相中的双分子反应看作是两个分子激烈碰撞的结果。在这里只学习简单的硬球碰撞理论 (SCT)。气相双分子简单反应如A+B→产物,2A→产物。 一、碰撞理论 1、微观模型 (1)反应物分子可看作简单的刚球,无内部结构: (2)分子间除碰撞间外无其它相互作用; (3)在反应过程中,反应分子的速率分布遵守麦克斯韦玻耳兹曼分布。 2、碰撞理论的基本要点 (1)分子必须通过碰撞才能发生反应,反应物分子间的接触碰撞是发生反应的前提。 即要反应,先碰撞; (2)不是任何两个反应物分子碰撞都能发生反应,只有当两个反应物碰撞分子的能量 超过一定的数值εo时,并满足一定的空间配布几何条件的碰撞反应才能发生反应: (3)活化分子的能量较普通能量高,它们碰撞时,松动并部分破坏了反应物分子中的 旧键,并可能形成新键,从而发生反应,这样的碰撞称为有效碰撞或非弹性碰撞,活化分 子愈多,发生化学反应的可能性就愈大。 根据上述的基本观点,自然得出一个结论:活化分子在单位时间内的碰撞就是反应速 率。 d[A]_ZB·q dt ZAB一(collision frequency)单位体积、单位时间内碰撞的分子数 q一(fraction of effective collision)有效碰撞在总碰撞中所占分数 设法求的Z和q就可求出r,碰撞理论就是求碰撞数Z和q。 简单碰撞理论是以硬球碰撞为模型,导出宏观反应速率常数的计算公式,故又称为硬 球碰撞理论
第十二章 化学动力学基础(二) 人们在测量了大量反应的速率常数,并对反应速率常数于温度的依赖关系有了相当了 解以后,对于为什么会有这些宏观规律存在必须从理论给予回答。在反应速率理论的发展 过程中,先后形成了碰撞理论、过渡态理论和单分子反应理论等。动力学理论与,发展较 迟。先后形成的碰撞理论、过渡态理论都是 20 世纪后建立起来的。而且与热力学的经典 理论相比尚有明显不足之处。 速度理论是研究化学反应的速率系数与温度的关系,描述反应过程的动力学性质。 速率理论的共同点:首先选定一个微观模型,用气体分子运动论(碰撞理论)或量子力 学(过渡态理论)的方法,并经过统计平均,导出宏观动力学中速率系数的计算公式。 由于所采用模型的局限性,使计算值与实验值不能完全吻合,还必须引入一些校正因 子,使理论的应用受到一定的限制。 §12.1 碰撞理论(Simple Collision theory)(SCT) 碰撞理论是接受了阿伦尼乌斯关于“活化状态”和“活化能”概念的基础上,利用已 经建立起来的气体分子运动论的基础上,在 20 世纪初由路易斯建立起来的。路易斯把气 相中的双分子反应看作是两个分子激烈碰撞的结果。在这里只学习简单的硬球碰撞理论 (SCT)。气相双分子简单反应如 A + B → 产物,2A → 产物。 一、碰撞理论 1、微观模型 (1) 反应物分子可看作简单的刚球,无内部结构; (2) 分子间除碰撞间外无其它相互作用; (3) 在反应过程中,反应分子的速率分布遵守麦克斯韦-玻耳兹曼分布。 2、碰撞理论的基本要点 (1) 分子必须通过碰撞才能发生反应,反应物分子间的接触碰撞是发生反应的前提。 即要反应,先碰撞; (2) 不是任何两个反应物分子碰撞都能发生反应,只有当两个反应物碰撞分子的能量 超过一定的数值ε0 时,并满足一定的空间配布几何条件的碰撞反应才能发生反应; (3)活化分子的能量较普通能量高,它们碰撞时,松动并部分破坏了反应物分子中的 旧键,并可能形成新键,从而发生反应,这样的碰撞称为有效碰撞或非弹性碰撞,活化分 子愈多,发生化学反应的可能性就愈大。 根据上述的基本观点,自然得出一个结论:活化分子在单位时间内的碰撞就是反应速 率。 A q AB d Z r dt L = − = ZAB—(collision frequency)单位体积、单位时间内碰撞的分子数 q — (fraction of effective collision)有效碰撞在总碰撞中所占分数 设法求的 Z 和 q 就可求出 r,碰撞理论就是求碰撞数 Z 和 q。 简单碰撞理论是以硬球碰撞为模型,导出宏观反应速率常数的计算公式,故又称为硬 球碰撞理论

二、双分子的互碰频率Z的求算 1、两个分子的一次碰撞过程 两个分子在相互的作用力下,先是互相接近,接近 到一定距离,分子间的斥力随着距离的减小而很快增大, 分子就改变原来的方向而相互远离,完成了一次碰撞过 程。粒子在质心体系中的碰撞轨线可用示意图表示为: 2、有效碰撞直径和碰撞截面 运动着的A分子和B分子,两者质心的投影落在直径为dAB的 圆截面之内,都有可能发生碰撞。两个分子的质心在碰撞过程所能 到达的最短距离称为有效直径(或碰撞直径)。其数值往往要稍大 B 于分子本身的直径。在分子碰撞理论中,采用了刚球模型,设A、B 两种分子都是完全弹性的、无压缩性的刚球,二者半径各为 2d24。,如图所示,A、B分子的有效碰撞直径dB,数 1 1 分子间的碰撞和有效直径 值上等于A分子和B分子的半径之和。d雄:)+)A 碰撞截面(oAB表示)为虚线圆的面积称,OAB=T·dAB2。 3、A与B分子互碰频率 设A分子数为NA,单位体积中的分子数为NAN,有效直径为dA,平均速率为uA; B分子数为NB,单位体积中的分子数为NBW,有效直径为dB,假定静止不动。 (I)先求出一个A分子以u速率与NB/V个静止B分子碰撞次数 将A分子看作是半径为dAB的分子,而将B看作是质点,若A以速率u运动,则在 t时间内扫过的体积为V=0ABua=T·dAB2·4at OAB=.dAB2 dAB=(dA+dB)/2 在单位时间内扫过的体积为V=V:=OAB·uA=T·dAB2·4A 假设B分子静止不动,则一个A分子以4速率与NN个静止B分子在单位体积、单 位时间内碰撞次数为 ZAB=0 AB UNa/V=I·dAB2·4 ANB/V Z8=OAB4 Na=πd (2)N个A分子以4速率与静止B分子碰撞次数 NAN个A分子以uA速率与NBN个静止B分子在单位体积、单位时间内碰撞次数为 Z=πd山,7 NA NB (3)NAN个A分子以u速率与NN个B分子速率为uR的碰撞次数 如果所有分子都在运动,则要用用A,B分子的平均相对运动速度山,代替A分子的平
二、双分子的互碰频率 Z 的求算 1、两个分子的一次碰撞过程 两个分子在相互的作用力下,先是互相接近,接近 到一定距离,分子间的斥力随着距离的减小而很快增大, 分子就改变原来的方向而相互远离,完成了一次碰撞过 程。粒子在质心体系中的碰撞轨线可用示意图表示为: 2、有效碰撞直径和碰撞截面 运动着的 A 分子和 B 分子,两者质心的投影落在直径为 dAB的 圆截面之内,都有可能发生碰撞。两个分子的质心在碰撞过程所能 到达的最短距离称为有效直径(或碰撞直径)。其数值往往要稍大 于分子本身的直径。在分子碰撞理论中,采用了刚球模型,设 A、B 两种分子都是完全弹性的、无压缩性的刚球,二者半径各为 A B 1 1 , 2 2 d d ,如图所示,A、B 分子的有效碰撞直径 dAB,数 值上等于 A 分子和 B 分子的半径之和。 AB A B 1 1 2 2 d d d = + 碰撞截面(σAB 表示)为虚线圆的面积称,σAB= π• dAB2 。 3、A 与 B 分子互碰频率 设 A 分子数为 NA ,单位体积中的分子数为 NA/V,有效直径为 dA,平均速率为 A u ; B 分子数为 NB ,单位体积中的分子数为 NB/V,有效直径为 dB,假定静止不动。 (1) 先求出一个 A 分子以 A u 速率与 NB/V 个静止 B 分子碰撞次数 将 A 分子看作是半径为 dAB的分子,而将 B 看作是质点,若 A 以速率 A u 运动,则在 t 时间内扫过的体积为 Vt=σAB• A u •t=π• dAB2 • A u •t σAB= π• dAB2 dAB=(dA+dB)/2 在单位时间内扫过的体积为 V = Vt /t =σAB• A u =π• dAB2 • A u 假设 B 分子静止不动,则一个 A 分子以 A u 速率与 NB/V 个静止 B 分子在单位体积、单 位时间内碰撞次数为 ZAB/=σAB• A u •NB/V =π• dAB2 • A u •NB/V 2 A A B B AB AB AB N N Z u d u V V = = ¢ (2) N 个 A 分子以 A u 速率与静止 B 分子碰撞次数 NA/N 个 A 分子以 A u 速率与 NB/V 个静止 B 分子在单位体积、单位时间内碰撞次数为 2 A A B AB AB N N Z d u V V = ⅱ (3) NA/V 个 A 分子以 A u 速率与 NB/V 个 B 分子速率为 B u 的碰撞次数 如果所有分子都在运动,则要用用 A,B 分子的平均相对运动速度 r u 代替 A 分子的平

均运动速度4。当A与B分子各自以平均运动速度u,作相对运动而发生碰撞时,可 以从0°到180°之间的任何角度彼此趋近。 A,B两分子的平均相对运动速度分别为 (a):两个分子运动方向一致4,=u+a (b):两个分子运动方向相反4,=4一4A (c):平均情况为两个分子以90°角互相碰撞 4=[+6]Ψ2 =(8= 8RT πms πMA 4g=( mg πMB 式中k一Boltzmann常数,R为气体常数。 将A和B分子看作硬球,根据气体分子运动论,它们以一定角度相碰,A,B分子的 平均相对运动速度 8RT 2 πMA 式中:一A,B分子的折合质量u=,单位为:kg·mo M+MR NAN个A分子以u速率与NB/N个速率为u的B分子在单位体积、单位时间内碰撞 次数为 Z=+r 互疏频率为乙=优告亡 8R7 或ZAB=πd 8RT [A][B] 因为=[A业 NB=[BIL 4、两个A分子的互碰频率 如果是同一种分子(两个A分子)的互碰时,系统中只有一种A分子,两个A分子互 碰的相对速度为:u,=(2× πM 每次碰撞需要两个A分子,为防止重复计算,在碰撞频率中除以2,所以两个A分子互 碰频率为: 8RT RT πM =2πd RT -[A] πM 在常温常压下,碰撞频率约为1035m3s 速率常数的推导 设有反应 A+B→P
均运动速度 A u 。当 A 与 B 分子各自以平均运动速度 A u , B u 作相对运动而发生碰撞时,可 以从 0°到 180°之间的任何角度彼此趋近。 A,B 两分子的平均相对运动速度分别为 (a):两个分子运动方向一致 r u = B u + A u (b):两个分子运动方向相反 r u = B u - A u (c):平均情况为两个分子以 90o角互相碰撞 2 2 1/ 2 A B 1/ 2 1/ 2 1/ 2 1/ 2 A B A A B B [ ] 8 8 8 8 ( ) ( ) ( ) ( ) r u u u kT RT kT RT u u m M m M = + = = = = 式中 k—Boltzmann 常数,R 为气体常数。 将 A 和 B 分子看作硬球,根据气体分子运动论,它们以一定角度相碰,A,B 分子的 平均相对运动速度 1/ 2 r A 8 ( ) RT u M = 式中μ—A,B 分子的折合质量 A B A B M M M M = + ,单位为:kg·mol-1 NA/N 个 A 分子以 A u 速率与 NB/V 个速率为 B u 的 B 分子在单位体积、单位时间内碰撞 次数为 2 2 2 1/ 2 A B [ ] A B AB AB N N Z d u u V V = + 互碰频率为: 2 A B AB AB N N 8RT Z d V V = 2 2 AB AB 8 [A][B] RT Z d L 或 = 因为 A B [A] [B] N N L L V V = = 4、两个 A 分子的互碰频率 如果是同一种分子(两个 A 分子)的互碰时,系统中只有一种 A 分子,两个 A 分子互 碰的相对速度为: 1/ 2 r A 8 (2 ) RT u M = 每次碰撞需要两个 A 分子,为防止重复计算,在碰撞频率中除以 2,所以两个 A 分子互 碰频率为: 2 2 A AA AA A 2 8 ( ) 2 N RT Z d V M = 2 2 A AA A 2 ( ) N RT d V M = 2 2 2 AA A 2 [A] RT d L M = 在常温常压下,碰撞频率约为 35 3 1 10 m s − − 速率常数的推导 设有反应 A B P + →