
2+9<0 (卡诺原理的数学表达式) 和 是两个过程中(等温)的热温商”。 T T 可逆卡诺循环的热温商: 2++9+Q4=0 卡诺定理推论:所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相等,即与 热机的工作物质无关。只与两热源的温度有关。 卡诺定理的意义: (1)引入了一个不等号n,<7,原则上解决了化学反应的方向问题; (2)解决了热机效率的极限值问题。 从卡诺循环得到的结论一熵的引入 【卡诺思想的局限性】 卡诺当时是用热质论来证明卡诺定理的,后来Kelvin和Claudius对卡诺的工作进行了 修正,用热力学第二定律重新证明了卡诺定理。 热力学第二定律虽然从理论上可以用来判别自然界一切过程进行的方向和限度,但具 体运用存在困难,需找到一种可定量描述的热力学函数,由其数值来直接判断过程的方向, 人们终于找到状态函数熵S。 -16-
- 16 - (卡诺原理的数学表达式) 1 1 T Q 和 2 2 T Q 是两个过程中(等温)的“热温商”。 可逆卡诺循环的热温商: 1 1 T Q + 2 2 T Q + 3 3 T Q + 4 4 T Q =0 卡诺定理推论:所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相等,即与 热机的工作物质无关。只与两热源的温度有关。 卡诺定理的意义: (1)引入了一个不等号 I R ,原则上解决了化学反应的方向问题; (2)解决了热机效率的极限值问题。 从卡诺循环得到的结论-熵的引入 【卡诺思想的局限性】 卡诺当时是用热质论来证明卡诺定理的, 后来 Kelvin 和 Claudius 对卡诺的工作进行了 修正, 用热力学第二定律重新证明了卡诺定理。 热力学第二定律虽然从理论上可以用来判别自然界一切过程进行的方向和限度, 但具 体运用存在困难,需找到一种可定量描述的热力学函数,由其数值来直接判断过程的方向. 人们终于找到状态函数熵 S

第二讲(2学时) 【教学目标】 1、掌握熵的定义的提出及意义。 2、熟悉Clausius不等式一热力学第二定律的数学表达式。 3、理解熵增加原理,掌握熵增加原理判断过程方向的方法。 4、了解热力学基本关系式和T-S图 5、掌握过程熵变计算的方法 【教学内容与时间分配】 3.3、熵的概念(0.5学时) 3.5、Clausius不等式与熵增加原理(0.5学时) 3.6、热力学基本关系式和T-S图(0.5学时) 3.7、熵变的计算(一)(0.5学时) 【本讲重点】 -17-
- 17 - 第二讲(2 学时) 【教学目标】 1、掌握熵的定义的提出及意义。 2、熟悉 Clausius 不等式-热力学第二定律的数学表达式。 3、理解熵增加原理,掌握熵增加原理判断过程方向的方法。 4、了解热力学基本关系式和 T-S 图 5、掌握过程熵变计算的方法 【教学内容与时间分配】 3.3、熵的概念(0.5 学时) 3.5、Clausius 不等式与熵增加原理(0.5 学时) 3.6、热力学基本关系式和 T-S 图(0.5 学时) 3.7、熵变的计算(一)(0.5 学时) 【本讲重点】

1、熵(变)的定义 2、热力学第二定律数学式(Clausius不等式) 【本讲难点】 1、熵概念的引入 2、第二定律的数学表达式 3、熵增加原理 【教学方式】 启发式+讲授+讨论+多媒体 3.4熵的概念 一、从卡诺循环得到的结论一熵的引入 a=-"-9+Q-I-1 T 1+g=1- e.T. 即:g+=0 亦即:Carnot循环中,热效应与热温商值的加和等于零。 现把可逆卡诺循环的结果推广到任意的可逆循环过程中。 1.任意可逆循环的热温商 任意可逆循环热温商的加和等于零,即:受。=0或〔8,2)。=0 证明如下: (I)在如图所示的任意可逆循环的曲线上取很靠近的PQ过程; (2)通过P,Q点分别作RS和TU两条可逆绝热膨胀 (3)在P,Q之间通过O点作等温可逆膨胀线W,使两个三角形PVO和OWQ的面积相等, 这样使PQ过程与PVOWO过程所作的功相同。 -18-
- 18 - 1、熵(变)的定义 2、热力学第二定律数学式(Clausius 不等式) 【本讲难点】 1、熵概念的引入 2、第二定律的数学表达式 3、熵增加原理 【教学方式】 启发式 + 讲授 + 讨论 + 多媒体 §3.4 熵的概念 一、从卡诺循环得到的结论— 熵的引入 h c h c R h h h W Q Q T T Q Q T − + − = = = 1 1 c c h h Q T Q T + = − 即: 0 c h c h Q Q T T + = 亦即:Carnot 循环中,热效应与热温商值的加和等于零。 现把可逆卡诺循环的结果推广到任意的可逆循环过程中。 1. 任意可逆循环的热温商 任意可逆循环热温商的加和等于零,即: R ( ) 0 i i i Q T = 或 0 δ R = T Q 证明如下: (1)在如图所示的任意可逆循环的曲线上取很靠近的 PQ 过程; (2)通过 P,Q 点分别作 RS 和 TU 两条可逆绝热膨胀 (3)在 P,Q 之间通过 O 点作等温可逆膨胀线 VW,使两个三角形 PVO 和 OWQ 的面积相等, 这样使 PQ 过程与 PVOWQ 过程所作的功相同
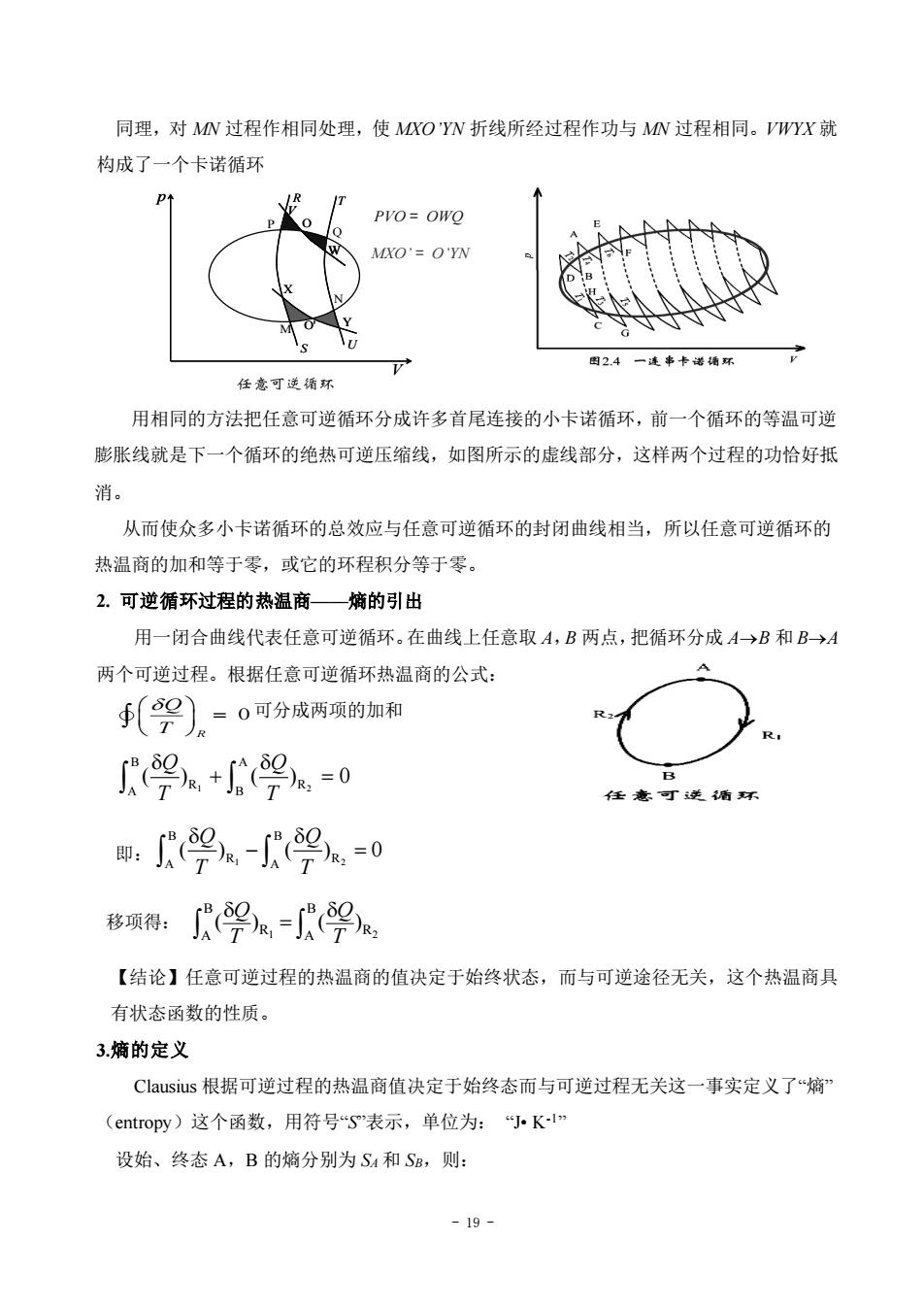
同理,对MN过程作相同处理,使MXO'YW折线所经过程作功与MN过程相同。VWYX就 构成了一个卡诺循环 PVO=OWO MXO=O'YN 图2.4一连串卡诺插环 任意可逆循环 用相同的方法把任意可逆循环分成许多首尾连接的小卡诺循环,前一个循环的等温可逆 膨胀线就是下一个循环的绝热可逆压缩线,如图所示的虚线部分,这样两个过程的功恰好抵 消。 从而使众多小卡诺循环的总效应与任意可逆循环的封闭曲线相当,所以任意可逆循环的 热温商的加和等于零,或它的环程积分等于零。 2.可逆循环过程的热温商—熵的引出 用一闭合曲线代表任意可逆循环。在曲线上任意取A,B两点,把循环分成A→B和B→A 两个可逆过程。根据任意可逆循环热温商的公式: ∮(架)。=0可分成两项的加和 9+9.=0 任意可逆盾环 即:9。-9a.=0 移项得: 2e-R 【结论】任意可逆过程的热温商的值决定于始终状态,而与可逆途径无关,这个热温商具 有状态函数的性质。 3.熵的定义 Clausius根据可逆过程的热温商值决定于始终态而与可逆过程无关这一事实定义了“熵 (entropy)这个函数,用符号S表示,单位为:小Kl 设始、终态A,B的熵分别为S4和SB,则: -19-
- 19 - 同理,对 MN 过程作相同处理,使 MXO’YN 折线所经过程作功与 MN 过程相同。VWYX 就 构成了一个卡诺循环 p V P Q M N X O' Y X O' Y T U T U R S R SO V W O V W V W PVO = OWQ MXO’ = O’YN 用相同的方法把任意可逆循环分成许多首尾连接的小卡诺循环,前一个循环的等温可逆 膨胀线就是下一个循环的绝热可逆压缩线,如图所示的虚线部分,这样两个过程的功恰好抵 消。 从而使众多小卡诺循环的总效应与任意可逆循环的封闭曲线相当,所以任意可逆循环的 热温商的加和等于零,或它的环程积分等于零。 2. 可逆循环过程的热温商——熵的引出 用一闭合曲线代表任意可逆循环。在曲线上任意取 A,B 两点,把循环分成 A→B 和 B→A 两个可逆过程。根据任意可逆循环热温商的公式: 0 R Q T = 可分成两项的加和 1 2 B A R R A B ( ) ( ) 0 Q Q T T + = 即: 1 2 B B R R A A ( ) ( ) 0 Q Q T T − = 移项得: 1 2 B B R R A A ( ) ( ) Q Q T T = 【结论】任意可逆过程的热温商的值决定于始终状态,而与可逆途径无关,这个热温商具 有状态函数的性质。 3.熵的定义 Clausius 根据可逆过程的热温商值决定于始终态而与可逆过程无关这一事实定义了“熵” (entropy)这个函数,用符号“S”表示,单位为: “J• K-1” 设始、终态 A,B 的熵分别为 SA 和 SB,则:

S-5=A=9。或A5=∑2。 △心-∑9=0 T 对微小变化: d=(9。 上式表明:当体系的状态变化时,其熵值的改变等于从始态到终态的任意可逆途径的 热温商之和,换言之可逆过程的热温商之和等于熵变。 说明:S和U、H一样,也是体系自身的性质,体系在一定的状态下就有一定的熵值。 当体系的状态变化时,要用可逆变化过程中的热温商来衡量它的改变量。 痛的特性: 1.是状态函数,是体系自身的性质: 2.S是一个广度性质(容量性质),总的△S等于各部分△S之和: 3.S单位在SI中是JK。 说明:第二定律只给△S、dS定义式,只发现体系有一状态函数S,但无法知道体系是给定 状态下熵的绝对值。 熵的定义是:△S 其物理含义:体系的熵变等于可逆过程的热温商之和。 熵的定义并不是对熵函数本身进行定义,而是定义熵的改变量等于可逆过程热温商之和, 而且。是用带有明显过程量性质的热量Q来对熵函数进行定义的。 用熵函数可以定量地判断自然界一切过程,包括化学反应过程,进行的方向和限度。 熵函数的应用已经远远超出自然科学的领域,可以说,一切科学领域都离不开熵。 S3.5 Clausius不等式与熵增加原理 一、Clausius不等式一热力学第二定律的数学表达式 前面所讨论的是可逆过程,而且从可逆过程中的热温商中定义了熵函数$ 设温度相同的两个高、低温热源间有一个可逆机和一个不可逆机(工,:高温热源,T: 低温热源)。 根据卡诺定律:7≤R 有9+№s-Ig+s0 2, -20-
- 20 - B B A R A ( ) Q S S S T − = = 或 R ( )i i i Q S T = R ( ) 0 i i i Q S T − = 对微小变化: d ( )R Q S T = 上式表明:当体系的状态变化时,其熵值的改变等于从始态到终态的任意可逆途径的 热温商之和,换言之可逆过程的热温商之和等于熵变。 说明:S 和U、H一样,也是体系自身的性质,体系在一定的状态下就有一定的熵值。 当体系的状态变化时, 要用可逆变化过程中的热温商来衡量它的改变量。 熵的特性: 1.是状态函数,是体系自身的性质; 2.S是一个广度性质(容量性质),总的ΔS等于各部分ΔS之和; 3.S单位在SI中是J ·K −1 。 说明:第二定律只给 ΔS、dS 定义式,只发现体系有一状态函数 S,但无法知道体系是给定 状态下熵的绝对值。 熵的定义是: R Q S T = 其物理含义:体系的熵变等于可逆过程的热温商之和。 熵的定义并不是对熵函数本身进行定义,而是定义熵的改变量等于可逆过程热温商之和, 而且。是用带有明显过程量性质的热量 QR来对熵函数进行定义的。 用熵函数可以定量地判断自然界一切过程,包括化学反应过程,进行的方向和限度。 熵函数的应用已经远远超出自然科学的领域,可以说,一切科学领域都离不开熵。 §3.5 Clausius 不等式与熵增加原理 一、Clausius 不等式——热力学第二定律的数学表达式 前面所讨论的是可逆过程,而且从可逆过程中的热温商中定义了熵函数 S 设温度相同的两个高、低温热源间有一个可逆机和一个不可逆机( T2 :高温热源, T1: 低温热源)。 根据卡诺定律: R 有 1 2 2 1 2 2 Q Q T T Q T + − 1 2 1 2 0 Q Q T T +