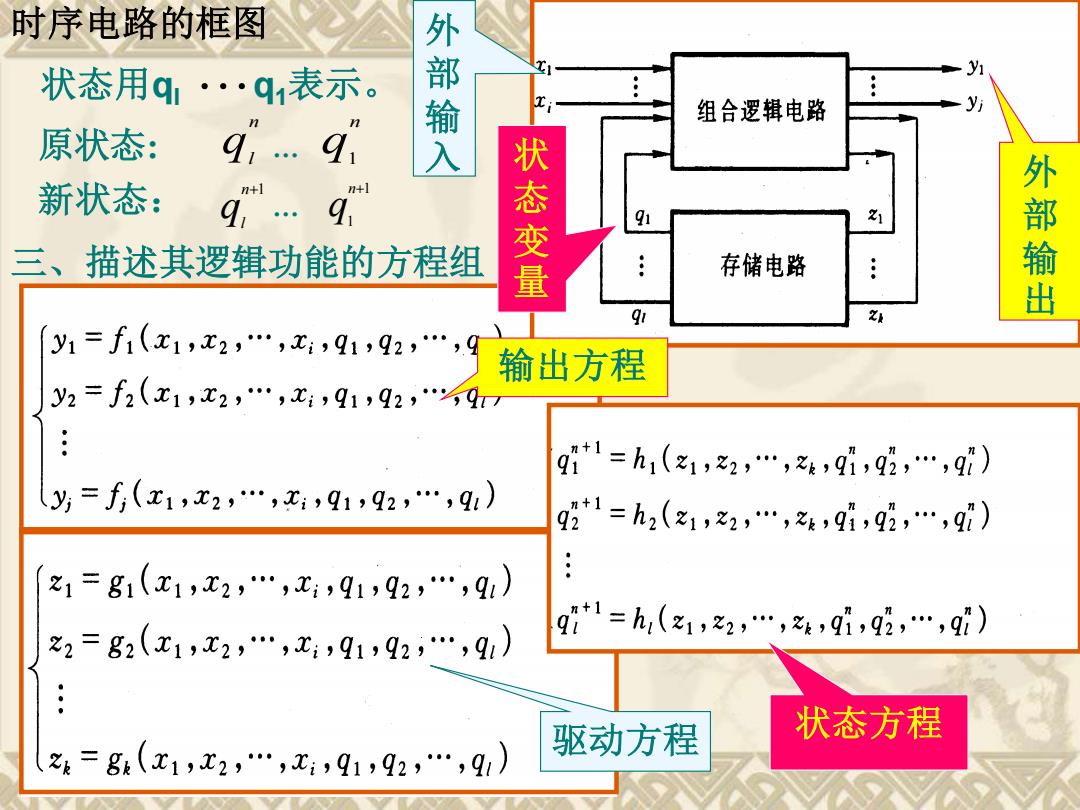
时序电路的框图 状态用q1…q表示。 外部输入 组合逻辑电路 原状态: 新状态: +] 4…91 三、描述其逻辑功能的方程组 状态变量 : 存储电路 外部输出 9r y1=f1(x1,x2,…,x,91,92,… 输出方程 y2=f2(x1,x2,…,x,q1,92,97 gi+1=h1(z1,之2,…,之4,9i,92,…,9i) y=f(x1,x2,…,x,91,92,…,91) 92*1=h2(z1,22,…,z4,9i,92,…,9) z1=g1(x1,x2,…,x:,91,92,…,91) gt1=h,(z1,之2,…,z4,9i,92,…,9) 之2=g2(x1,x2,…,t,91,92,…,91) : 状态方程 之4=g(x1,2,…,x,91,92,…,9) 驱动方程
时序电路的框图 外 部 输 入 外 部 输 出 原状态: q n q 1 n l … 新状态: q n 1 1 + q n l +1 … 三、描述其逻辑功能的方程组 驱动方程 状 态 变 量 输出方程 状态方程 状态用ql q1表示

三、功能描述 用三个方程描述 1、输出方程 Y(n)=F[x()ot】 外部输出=外输入和内输入组合函数 2、激励方程 Zt)=Gx(n)b94】 触发器的输入信号的逻辑表达式 例如:J=A,K=B 3、状态方程 Q4n)=H[Zln,】 将存储电路中每个触发器的输入信号的逻辑表达式(激励 方程)代入相应触发器的特征方程,其结果就是触发器状态 方程。 例如JK触发器特征方程:Q”1=JQ”+KQ' 将激励方程J=A,K=B代入其状态方程Q1=AQ”+BO
三、功能描述 1、输出方程 外部输出=外输入和内输入组合函数 触发器的输入信号的逻辑表达式 2、激励方程 将存储电路中每个触发器的输入信号的逻辑表达式(激励 方程)代入相应触发器的特征方程,其结果就是触发器状态 方程。 3、状态方程 用三个方程描述 ( ) ( ) ( ) n n n Y t = F X t ,Q t ( ) ( ) ( ) n n n Z t = G X t ,Q t ( ) ( ) ( ) n n n Q t H Z t ,Q t +1 = 例如:J = A,K = B n n n Q = JQ + KQ +1 n n = AQ + BQ n+1 其状态方程 Q 例如JK触发器特征方程: 将激励方程J = A,K = B代入

四、时序电路的分类 同步时序逻辑电路; 按电路中触发器的动作特点可分为: 异步时序逻辑电路。 同步时序逻辑电路:电路中所有触发器状态的变化都在同一 时钟信号的同一边沿发生。 异步时序逻辑电路:不满足同步时序逻辑电路的条件。 ·不在同一时钟边沿翻转; ·没有时钟信号。 按输出信号的特点分,可分为米利型(Mealy)和 穆尔型(Moore) 两种 米利型:输出信号与电路的状态和输入变量都有关。 穆尔型:输出信号只取决于电路的状态。 (电路可能没有输入信号)
四、时序电路的分类 同步时序逻辑电路:电路中所有触发器状态的变化都在同一 时钟信号的同一边沿发生。 异步时序逻辑电路:不满足同步时序逻辑电路的条件。 • 不在同一时钟边沿翻转; • 没有时钟信号。 按输出信号的特点分,可分为米利型(Mealy)和 穆尔型(Moore)两种。 米利型:输出信号与电路的状态和输入变量都有关。 穆尔型:输出信号只取决于电路的状态。 (电路可能没有输入信号)。 按电路中触发器的动作特点可分为:同步时序逻辑电路; 异步时序逻辑电路
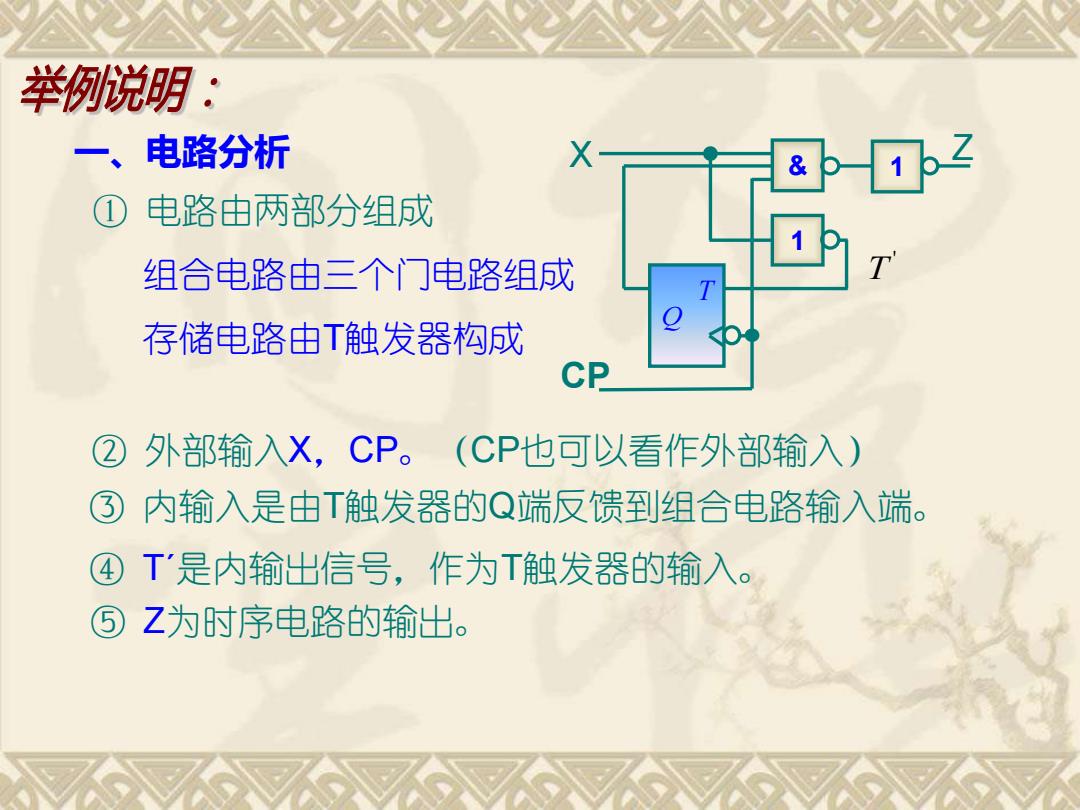
举例说明: 一、电路分析 X & 1b2 ① 电路由两部分组成 组合电路由三个门电路组成 存储电路由T触发器构成 ② 外部输入X,CP。(CP也可以看作外部输入) 内输入是由T触发器的Q端反馈到组合电路输入端。 ④ T'是内输出信号,作为T触发器的输入。 ⑤Z为时序电路的输出
一、电路分析 ① 电路由两部分组成 ② 外部输入X,CP。(CP也可以看作外部输入) ③ 内输入是由T触发器的Q端反馈到组合电路输入端。 ④ Tˊ是内输出信号,作为T触发器的输入。 ⑤ Z为时序电路的输出。 组合电路由三个门电路组成 存储电路由T触发器构成 Z Q T & 1 X 1 CP ' T
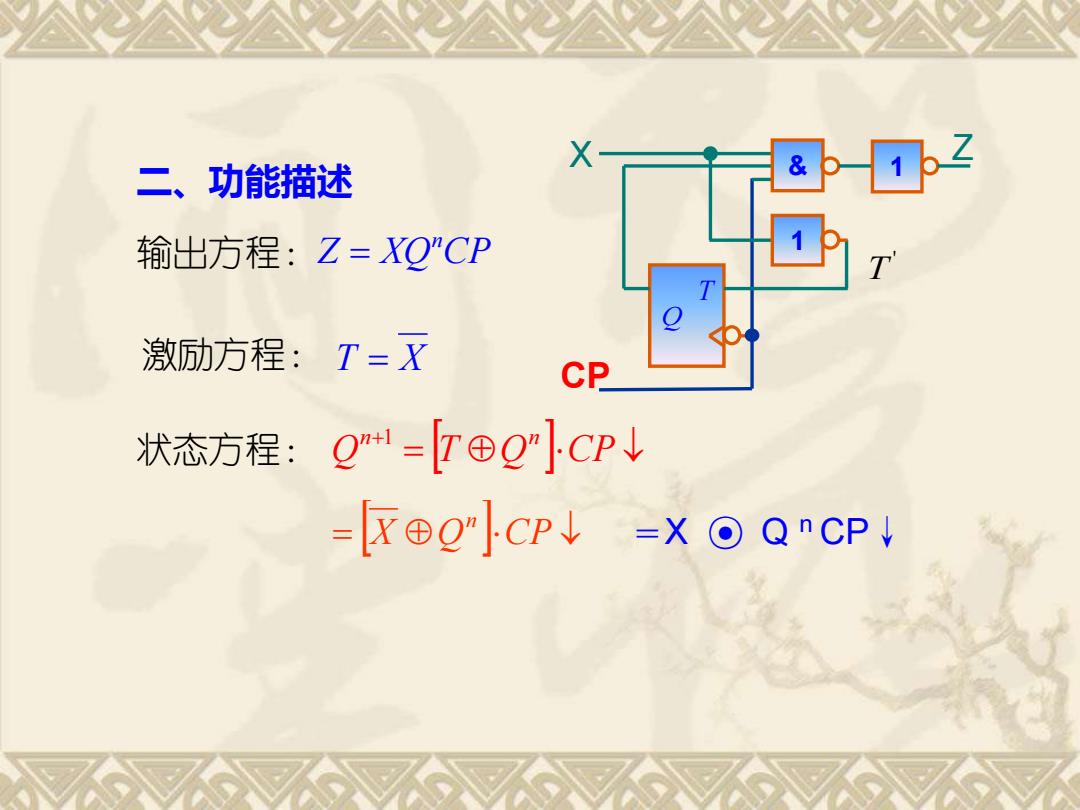
X 二、功能描述 & 2 输出方程:Z=XOCP 激励方程:T=X CP 状态方程: Q=T⊕Q]CpU =K⊕OCP↓=X⊙QnCP↓
二、功能描述 输出方程: Z XQ CP n = 激励方程: T = X 状态方程: = + Q T Q CP n 1 n = X Q CP n =X ⊙ Q n CP↓ Q T & 1 X 1 CP ' T Z