
基本概念 随机变量:取值随机、而在确定范围内取值具有确 定概率的变量 随机变量的分布:随机变量的大量取值所表现出的 统计规律性 概率密度函数(PDF):函数化的随机变量分布, 通常以p表示。 累积分布函数(CDF):PDF的积分,通常以P表示 P()=广poa
随机变量:取值随机、而在确定范围内取值具有确 定概率的变量 随机变量的分布:随机变量的大量取值所表现出的 统计规律性 概率密度函数(PDF):函数化的随机变量分布, 通常以 p 表示。 累积分布函数(CDF):PDF的积分,通常以 P 表示 基本概念
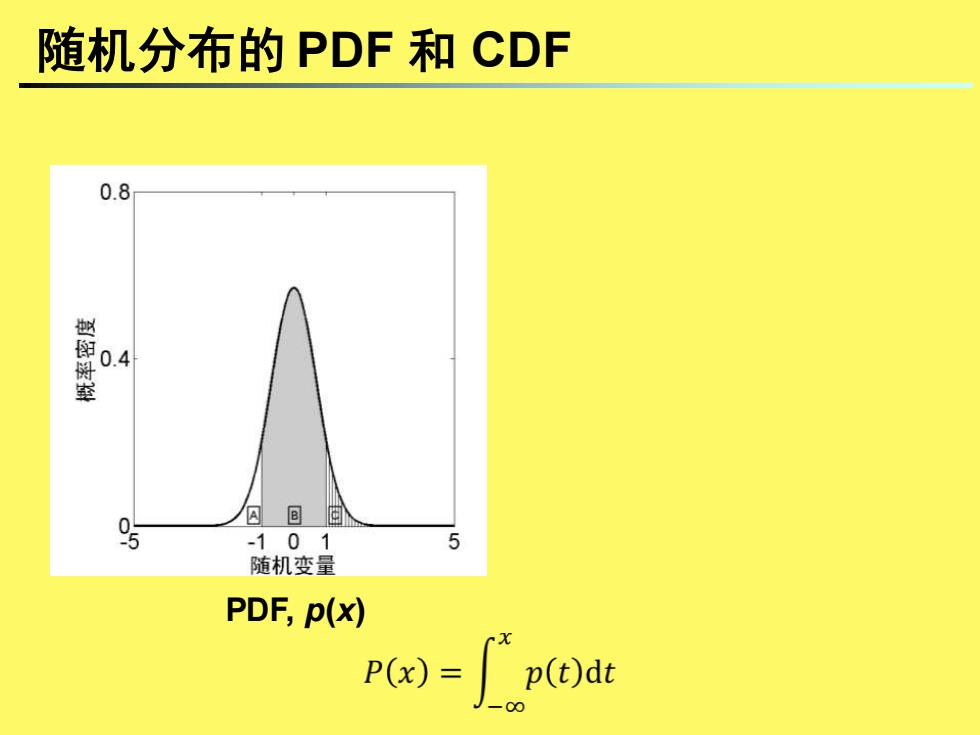
随机分布的PDF和CDF 0.8 0.4 囚回间 -101 5 随机变量 PDF,p(x) P(x)= p()dt
随机分布的 PDF 和 CDF PDF, p(x) CDF, P(x)

正态分布 正态分布(normal distribution),表示为 N(4,o2);概率密度函数(PDF)为高斯函数。 (x-u)2 p(x)= 2G2 0√2元 p一概率密度; x一测量值 一总体平均值;σ一标准偏差
正态分布 正态分布 (normal distribution) ,表示为 N(, 2 );概率密度函数 (PDF) 为高斯函数 。 p — 概率密度; x — 测量值 μ — 总体平均值; σ — 标准偏差

(1)极大值处在x=4,表明大多数测量值在4附 近,即平均值能够较好地反映数据的集中趋势; 1 (2)Pmax= √2元,概率密度的极大值取决于。: (3)以x=”成镜面对称,说明正负误差出现的概 率相等; (4)x→士o0时,y→0,说明极大误差出现的概率 为0。 9
9 (2) ,概率密度的极大值取决于σ; (1)极大值处在 x = μ, 表明大多数测量值在 μ 附 近,即平均值能够较好地反映数据的集中趋势; (3)以 x = μ 成镜面对称,说明正负误差出现的概 率相等; (4) 时,y→0,说明极大误差出现的概率 为0。 x →
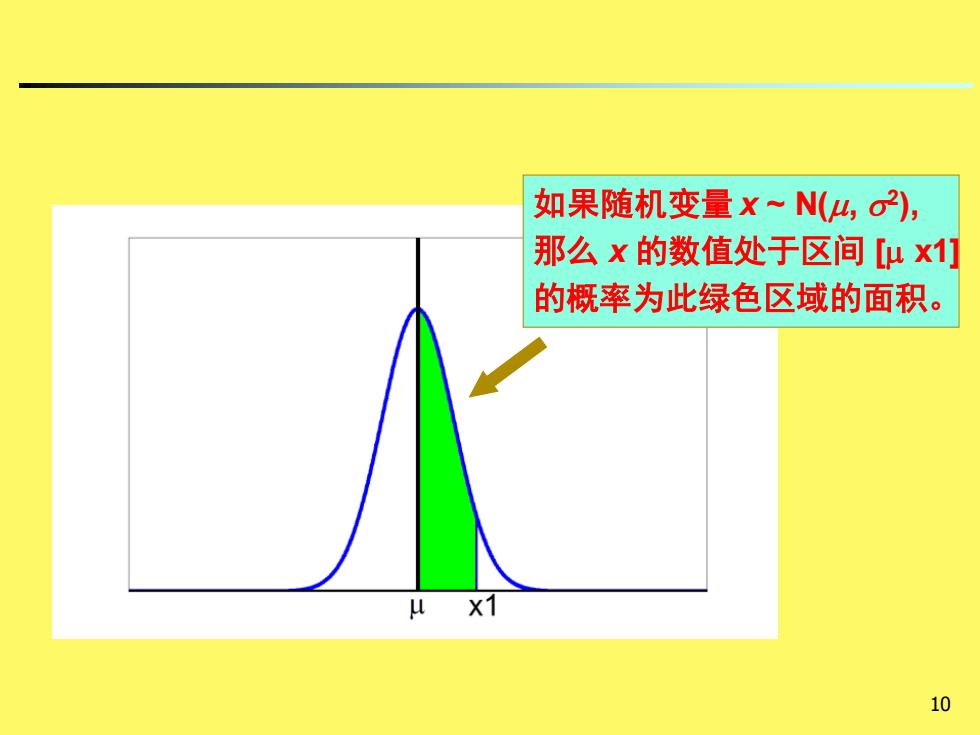
如果随机变量X~N(山,o2), 那么x的数值处于区间[μx1] 的概率为此绿色区域的面积。 10
10 如果随机变量 x ~ N(, 2 ), 那么 x 的数值处于区间 [ x1] 的概率为此绿色区域的面积