
❖总曳力 ❖颗粒雷诺数 ——斯托克斯(Stockes)定律 sin cos D S F w A A F F F dA pdA = + = + Re p p d u = 4-1 流体绕过颗粒及颗粒床层的流动 ◼ 曳力与雷诺数
❖总曳力 ❖颗粒雷诺数 ——斯托克斯(Stockes)定律 sin cos D S F w A A F F F dA pdA = + = + Re p p d u = 4-1 流体绕过颗粒及颗粒床层的流动 ◼ 曳力与雷诺数
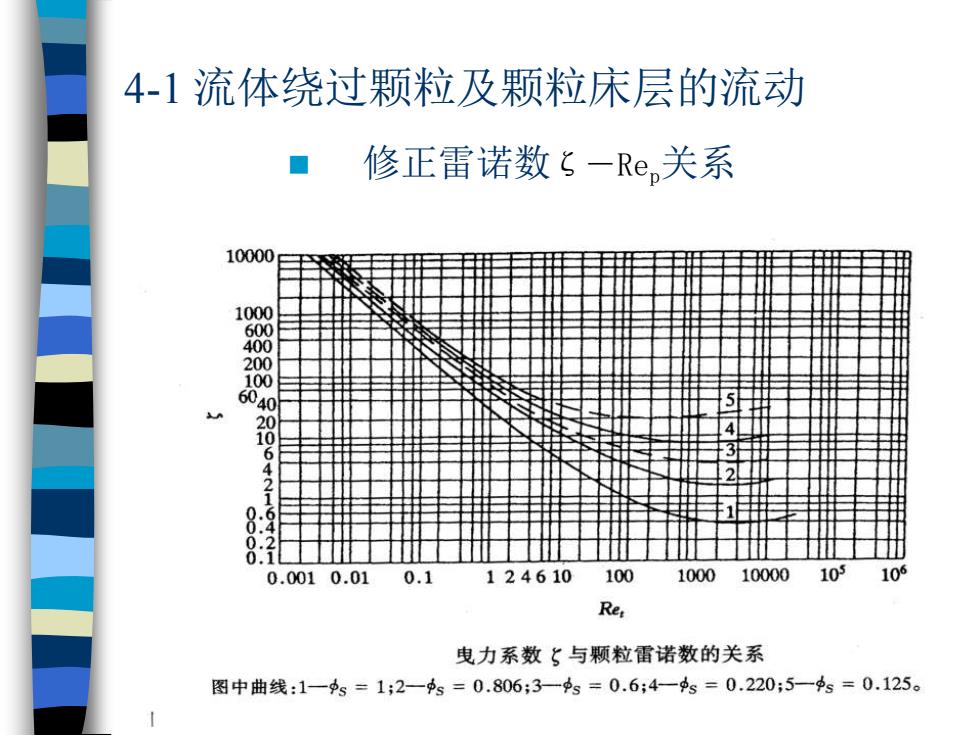
◼ 修正雷诺数ζ-Rep关系 4-1 流体绕过颗粒及颗粒床层的流动
◼ 修正雷诺数ζ-Rep关系 4-1 流体绕过颗粒及颗粒床层的流动
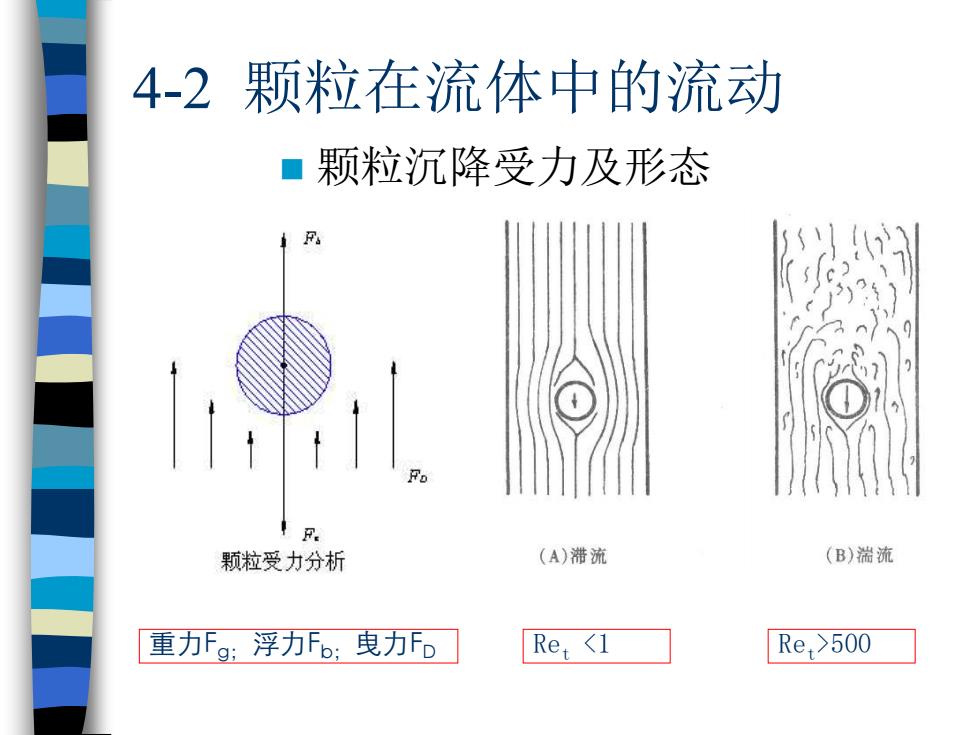
4-2 颗粒在流体中的流动 ◼ 颗粒沉降受力及形态 重力Fg; 浮力Fb; 曳力FD Ret Re >500 t <1
4-2 颗粒在流体中的流动 ◼ 颗粒沉降受力及形态 重力Fg; 浮力Fb; 曳力FD Ret Re >500 t <1
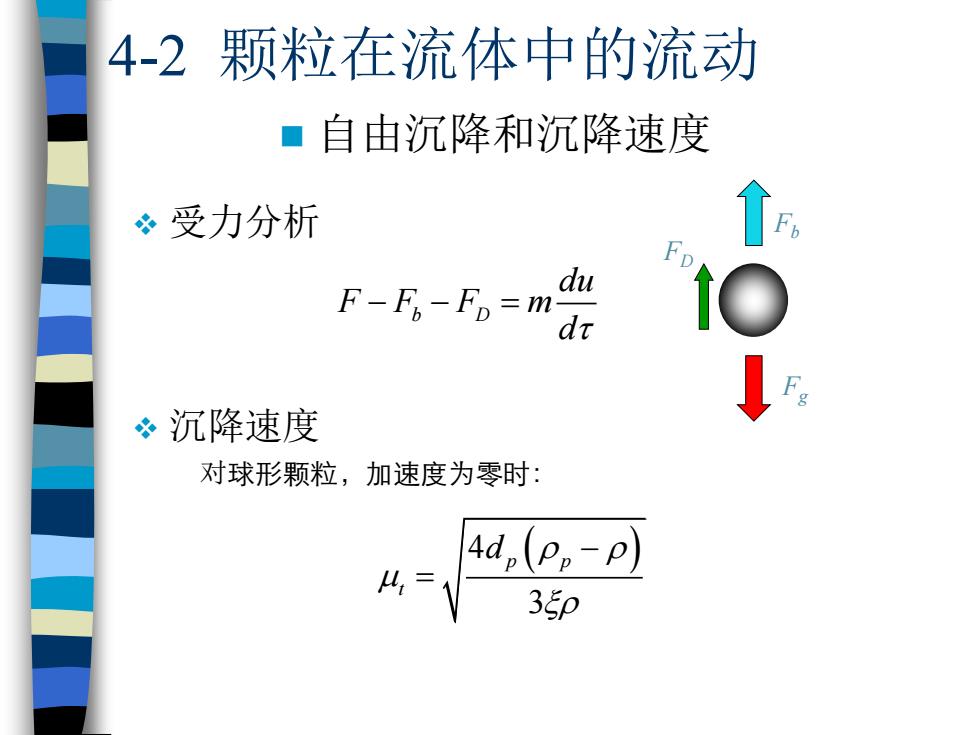
❖ 受力分析 ❖ 沉降速度 对球形颗粒,加速度为零时: 4-2 颗粒在流体中的流动 ◼ 自由沉降和沉降速度 4 ( ) 3 p p t d − = b D du F F F m d − − = Fg Fb FD
❖ 受力分析 ❖ 沉降速度 对球形颗粒,加速度为零时: 4-2 颗粒在流体中的流动 ◼ 自由沉降和沉降速度 4 ( ) 3 p p t d − = b D du F F F m d − − = Fg Fb FD

◼ 沉降速度计算方法 ❖试差法 ➢滞流区(Rep或Ret <1): ➢过渡区(1≤Rep(或Ret)≤500): ➢湍流区(500< Rep(或Ret)<2×105): ❖摩擦因数群法(图解法) ( ) 2 18 p p t d g − = ( ) 5 1.6 7 0.4 0.6 0.154 p p t d g − = ( ) 1.74 p p t d g − = ➢计算实例见教材P287例4-1和4-2
◼ 沉降速度计算方法 ❖试差法 ➢滞流区(Rep或Ret <1): ➢过渡区(1≤Rep(或Ret)≤500): ➢湍流区(500< Rep(或Ret)<2×105): ❖摩擦因数群法(图解法) ( ) 2 18 p p t d g − = ( ) 5 1.6 7 0.4 0.6 0.154 p p t d g − = ( ) 1.74 p p t d g − = ➢计算实例见教材P287例4-1和4-2