
§1.4 Maxwell分布律
§1.4 Maxwell 分布律
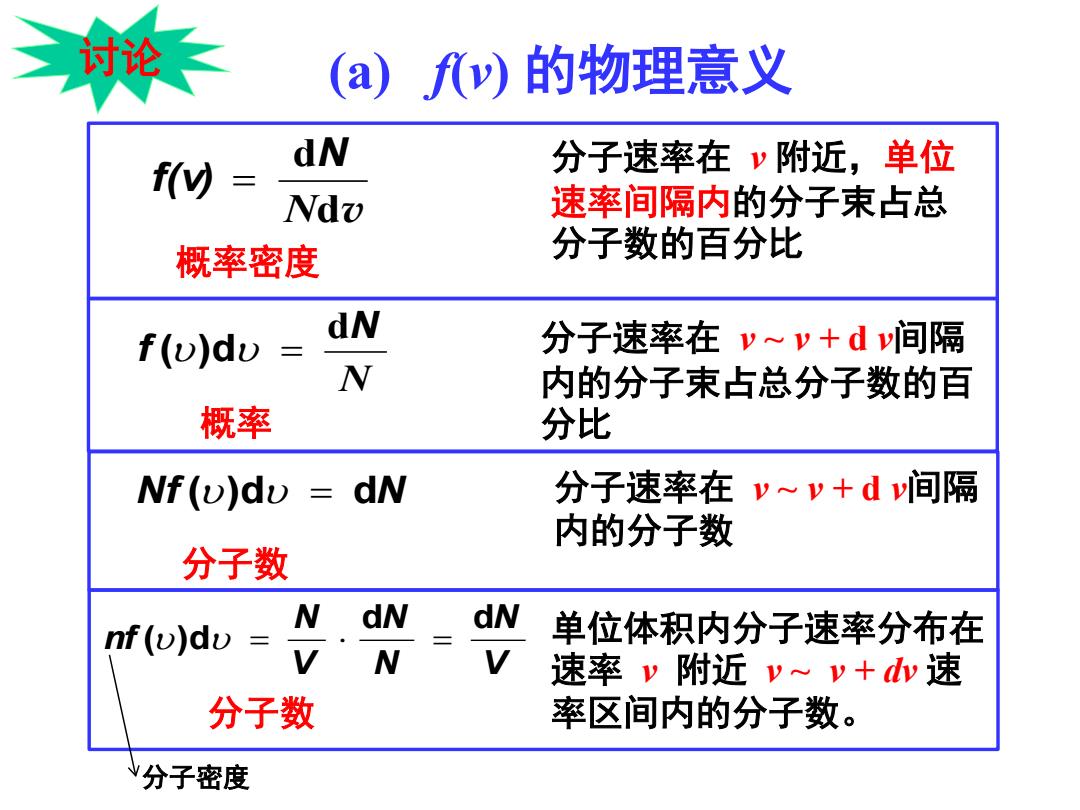
三讨论← (a)fv)的物理意义 f(y) dN 分子速率在v附近,单位 Ndo 速率间隔内的分子束占总 概率密度 分子数的百分比 f(v)dv dN 分子速率在v~v+dv间隔 N 内的分子束占总分子数的百 概率 分比 Nf(v)du dN 分子速率在v~v+d间隔 内的分子数 分子数 nf(v)dv N dN dN 单位体积内分子速率分布在 V N 速率v附近v~v+dw速 分子数 率区间内的分子数。 分子密度
dv d N N f(v) = (a) f(ν) 的物理意义 概率密度 分子速率在 ν 附近,单位 速率间隔内的分子束占总 分子数的百分比 N N f d (υ)dυ = 概率 分子速率在 ν ~ ν + d ν间隔 内的分子束占总分子数的百 分比 Nf (υ)dυ = dN 分子数 分子速率在 ν ~ ν + d ν间隔 内的分子数 讨论 单位体积内分子速率分布在 速率 v 附近 v ~ v + dv 速 分子数 率区间内的分子数。 V N N N V N nf d d (υ)dυ = ⋅ = 分子密度

讨论 分布在有限速率区间y1~y2 内的分子数占总分子数的比 率。 N(d 分布在有限速率区间y,~2 内的分子数。 f)d=1 分布在0~∞速率区间内的 分子数占总分子数的比率。 (归一化条件) 。v2f()a=v2 w2的平均值
分布在有限速率区间v1 ~ v2 内的分子数占总分子数的比 率。 分布在有限速率区间 v1 ~ v2 内的分子数。 分布在 0 ~ ∞ 速率区间内的 分子数占总分子数的比率。 ( 归一化条件) v2 的平均值。 2 2 1 1 ( ) ( ) 4. ( ) v N v v N v dN f v dv N = ∫ ∫ 2 2 1 1 ( ) ( ) 5. ( ) v N v v N v Nf v dv dN = ∫ ∫ 0 6. ( ) 1 f v dv ∞ = ∫ 2 2 0 7. ( ) v f v dv v ∞ = ∫ 讨论

讨论 (b)f(v)的性质 ∫f(o)dw=1归-性质 (=00) dN, (o=0) W
υ dυ ∫ ∞ 0 f ( ) ( ) ( ) ∫ =∞ = = υ υ υ 0 N dN =1 归一性质 讨论 (b) f (v ) 的性质 4
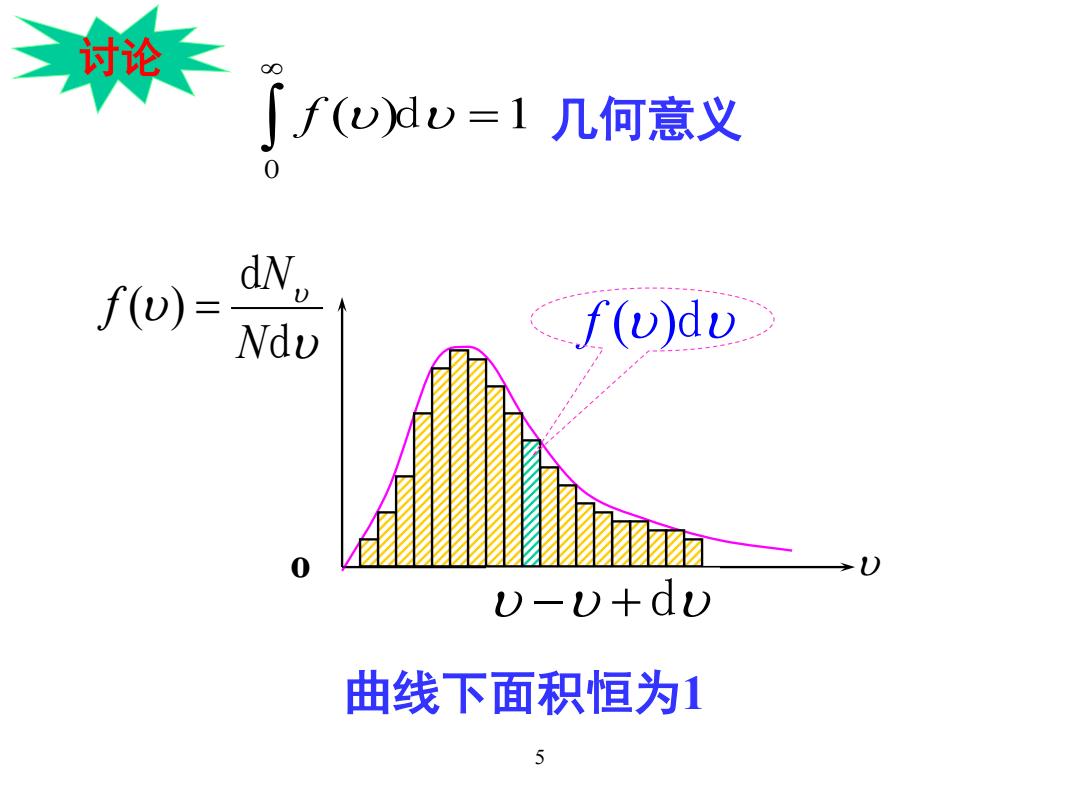
讨论 00 ∫f(ww=1几何意义 dN. f(w)= Ndu f(v)du 0 1) )-)+d) 曲线下面积恒为1 5
曲线下面积恒为1 ( ) 1 0 = ∫ ∞ f υ dυ 几何意义 o υ υ υ Δ Δ N N υ υ +Δυ υ υ υ d d N N f ( ) = υ −υ + dυ o f ( ) υ υd 讨论 5