讨论年 速率介于yy,之间的气体分子的平均速率的计算 f f"f(v)dv 只,n主f) 对于v的某个函数g(y,一般地,其平均值可以表示为 90 g(y)= ∫fdw
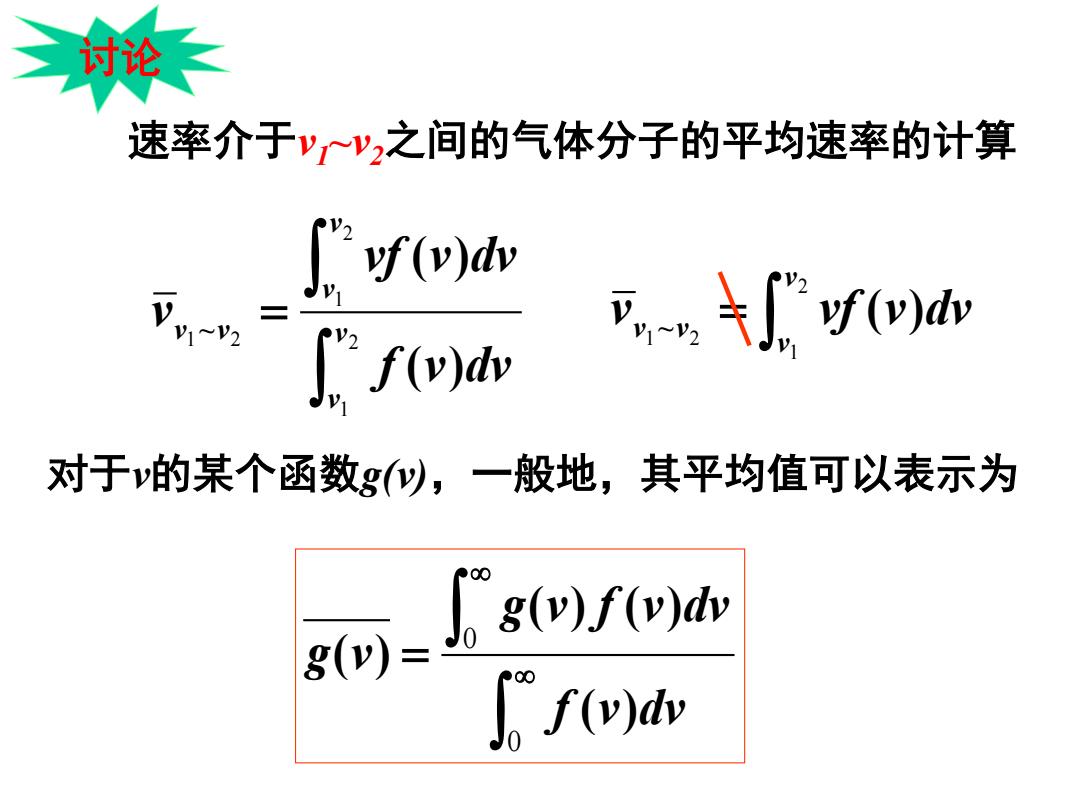
速率介于v1~v2之间的气体分子的平均速率的计算 ∫ ∫ = 2 1 2 1 1 2 v v v v v v f v dv vf v dv v ( ) ( ) ~ ∫ = 2 1 1 2 v v v v v vf (v)dv ~ 对于v的某个函数g(v),一般地,其平均值可以表示为 ∫ ∫ ∞ ∞ = 0 0 f v dv g v f v dv g v ( ) ( ) ( ) ( ) 讨论

三讨论 2)平均值的计算公式 注意上下区间的一致性 -Sif(v)dv 全空间 fNf(d ∫f(w)du 7
2) 平均值的计算公式 注意上下区间的一致性 ∫ ∞ = 0 υ υf (υ)dυ ∫ ∫ = 2 1 2 1 ( ) ( ) υ υ υ υ υ υ υ υ υ υ d d Nf Nf ∫ ∫ = 2 1 2 1 ( ) ( ) υ υ υ υ υ υ υ υ υ d d f f 全空间 讨论 7
讨论← 1) uf(u)du 0 规律:任意v的函数o(v)对全体分子 的平均值都可以用速率分布函数由上式 求得: 00 p(o)=∫p(v)f(w)dv 量子力学中还会碰到类似计算
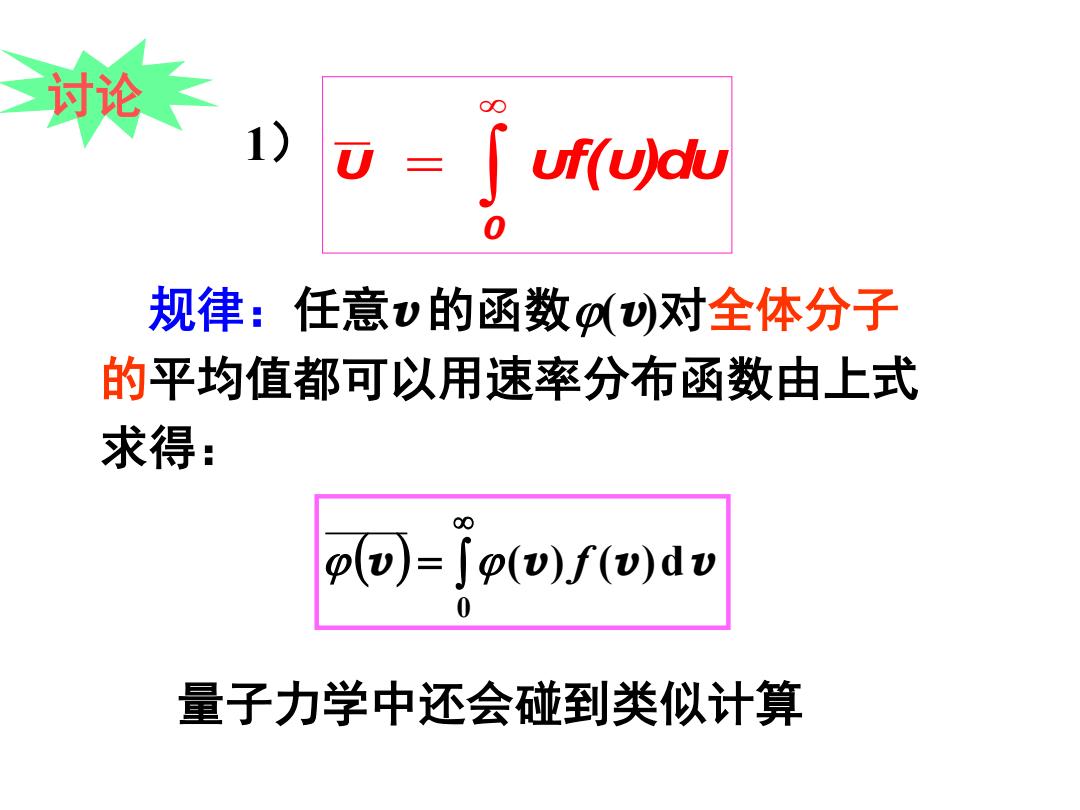
规律:任意v 的函数ϕ(v)对全体分子 的平均值都可以用速率分布函数由上式 求得: ( ) ∫ ∞ = 0 ϕ v ϕ(v ) f (v )dv υ υf(υ)dυ 0 ∫ ∞ = 量子力学中还会碰到类似计算 讨论 1)
(一) 速度分布函数 d d dn(vx,vy,v) 2 F(vx,Vy,Vz)= V Ndv.do,do. 物理意义: 速度出现在v(,卫,)点附近, 单位速度空间体积内的分子数 占系统分子总数的百分比 或,一个分子的速度出现在单位速度空间 体积内的概率 分子在速度空间分布的概率密度
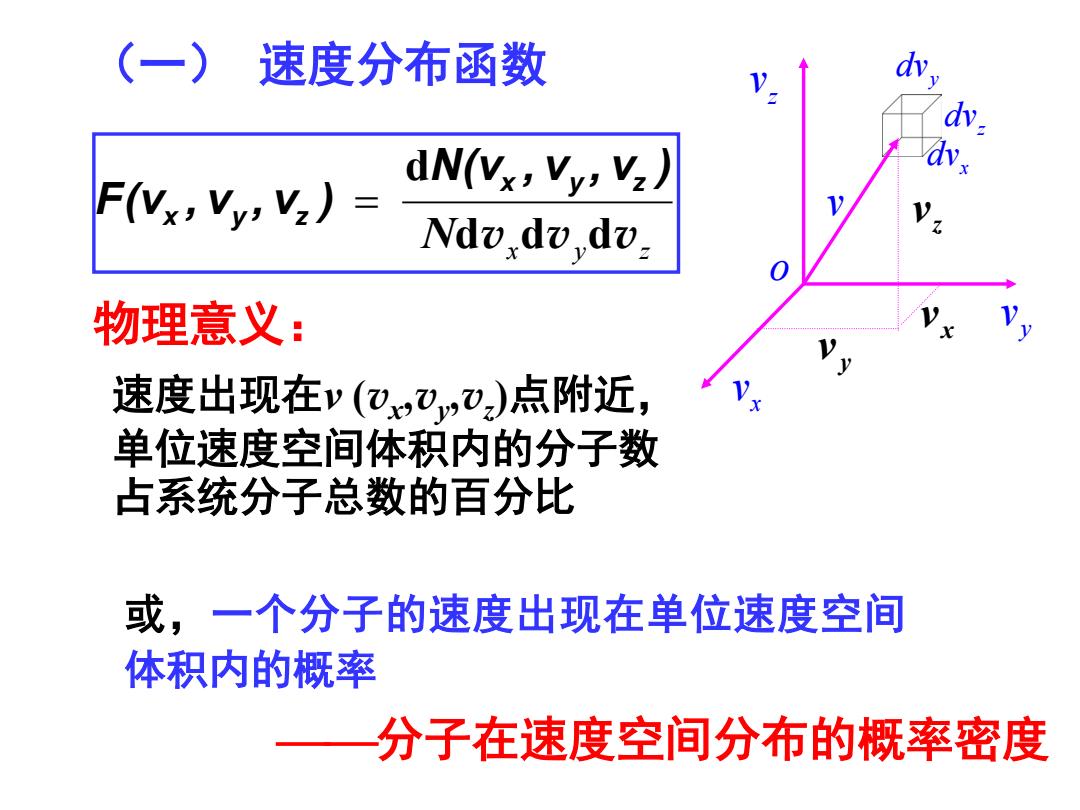
(一) 速度分布函数 dvxdvydvz d N N(v , v , v ) F(v , v , v ) x y z x y z = 或,一个分子的速度出现在单位速度空间 体积内的概率 物理意义: 分子在速度空间分布的概率密度 x v z v y v x v z v y v x dv z dv y dv o v 速度出现在v (vx,vy,vz)点附近, 单位速度空间体积内的分子数 占系统分子总数的百分比